翻译：

蒙德施塔特一个酒庄帝国的大亨，在任何方面都无可匹敌。法佛尼乌斯骑士团中具有异域外表的思想家。

这一次，兄弟俩要处理的是一块刻着他们名字的奇怪木头。这块木板可以表示为一串𝑛字符。每个字符不是“D”就是“K”。您希望在这个字符串上进行一些切割(可能是0)，将它划分为几个连续的片段，每个片段的长度至少为1。兄弟俩做事都很有尊严，所以他们想把木头尽可能平均地劈开。他们想知道你能把木头分成的最大块数，使每一块中出现D的次数与出现K的次数之比相等。

Kaeya是一个好奇的思考者，他对多种场景的解决方案感兴趣。他想知道给定字符串的每个前缀的答案。帮他解决这个问题!

对于字符串，我们将比率定义为𝑎:𝑏，其中'D'出现𝑎次，'K'出现𝑏次。注意𝑎或𝑏可以等于0，但不能同时等于0。比率𝑎:𝑏𝑐:𝑑被认为是相等当且仅当𝑎⋅𝑑=𝑏⋅𝑐。

例如，对于字符串'DDD'，比例将是3:0，对于'DKD' - 2:1，对于'DKK' - 1:2，对于' kkkdd ' - 2:4。请注意，后两个字符串的比值是相等的，但它们不等于前两个字符串的比值。

输入
每个测试包含多个测试用例。第一行包含测试用例的数量𝑡(1≤𝑡≤1000)。测试用例的描述如下。

每个测试用例的第一行包含整数𝑛(1≤𝑛≤5⋅105)——木料的长度。

每个测试用例的第二行包含一个长度为𝑛的字符串𝑠。𝑠的每个字符要么是“D”，要么是“K”。

保证𝑛在所有测试用例上的总和不超过5⋅105。

输出
对于每个测试用例，输出𝑛空格分隔的整数。这些数字的𝑖-th应该等于前缀𝑠1，𝑠2，…，𝑠𝑖的答案。

例子
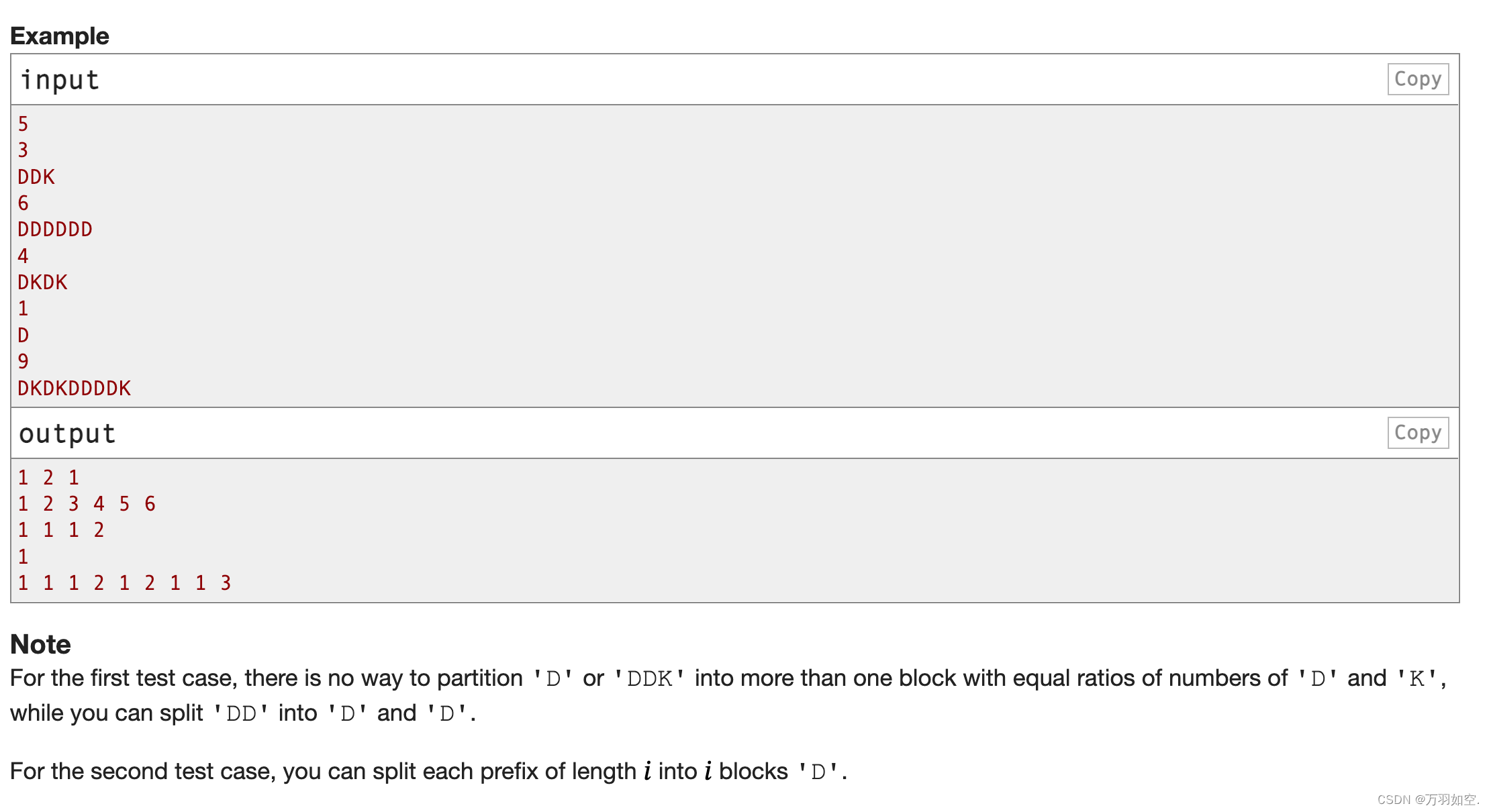
inputCopy
5
3.
DDK
6
DDDDDD
4
DKDK
1
D
9
DKDKDDDDK
outputCopy
1 2 1
1 2 3 4 5 6
1 1 1 2
1
1 1 1 2 1 2 1 1 3
请注意
对于第一个测试用例，没有办法将“D”或“DDK”划分为多个具有相同数量比例的“D”和“K”的块，而您可以将“DD”划分为“D”和“D”。

对于第二个测试用例，您可以将每个长度为𝑖的前缀分割为𝑖块“D”。

思路：每次划分前缀，相同等比例的最大值，我们可以每次记录比例的次数，因为我们可以容易得出这样的一个结论，当D：K=1:2，等后面比例再次到达D：K=1:2，那么中间这一段也一定是D：K=1:2。所以我们每次记录前边比例的出现的次数，当前的最大的就是之前同比例的累加中最大的。

代码：

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
ll  gcd(ll a,ll b)
{
    if (b==0) {
        return a;
    }
    return gcd(b, a%b);
}

string s;
void solv(){
    cin>>n;
    cin>>s;
    map<pair<int, int>,int>q;
    int d=0,k=0;
    for (int i=0; i<n; i++) {
        if (s[i]=='D') {
            d++;
        }
        if (s[i]=='K') {
            k++;
        }
        int jk=gcd(d, k);
        q[{d/jk,k/jk}]++;
        printf("%d ",q[{d/jk,k/jk}]);
        
    }printf("\n");
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}