线段树的概念

线段树（Segment Tree）是一种平衡二叉树，用于解决区间查询问题。它将一个区间划分成若干个子区间，从而实现对整个区间的快速查询和修改。线段树可以表示固定区间上的某种信息，例如区间和、区间最大值、区间最小值等。每个非叶子节点维护其子节点所包含区间的信息，所以，线段树可以高效地处理区间查询和区间修改等操作。

线段树可以应用于多种场景，比如对于静态问题可以使用单次建树的线段树，对于动态问题可以使用可持久化线段树，在此基础上实现区间修改和查询的历史版本记录。线段树还可以结合线段树的优化技巧来达到更高的效率，例如使用线性预处理、差分、前缀和等技巧降低查询和修改的时间复杂度，利用分支预测和循环展开降低分支跳转的代价等。

线段树的实现

线段树的每一个节点都表示一个区间，设区间被mid分割，则mid左边的范围表示节点左子树的区间，右边的范围表示节点右子树的区间。具体图例如下。

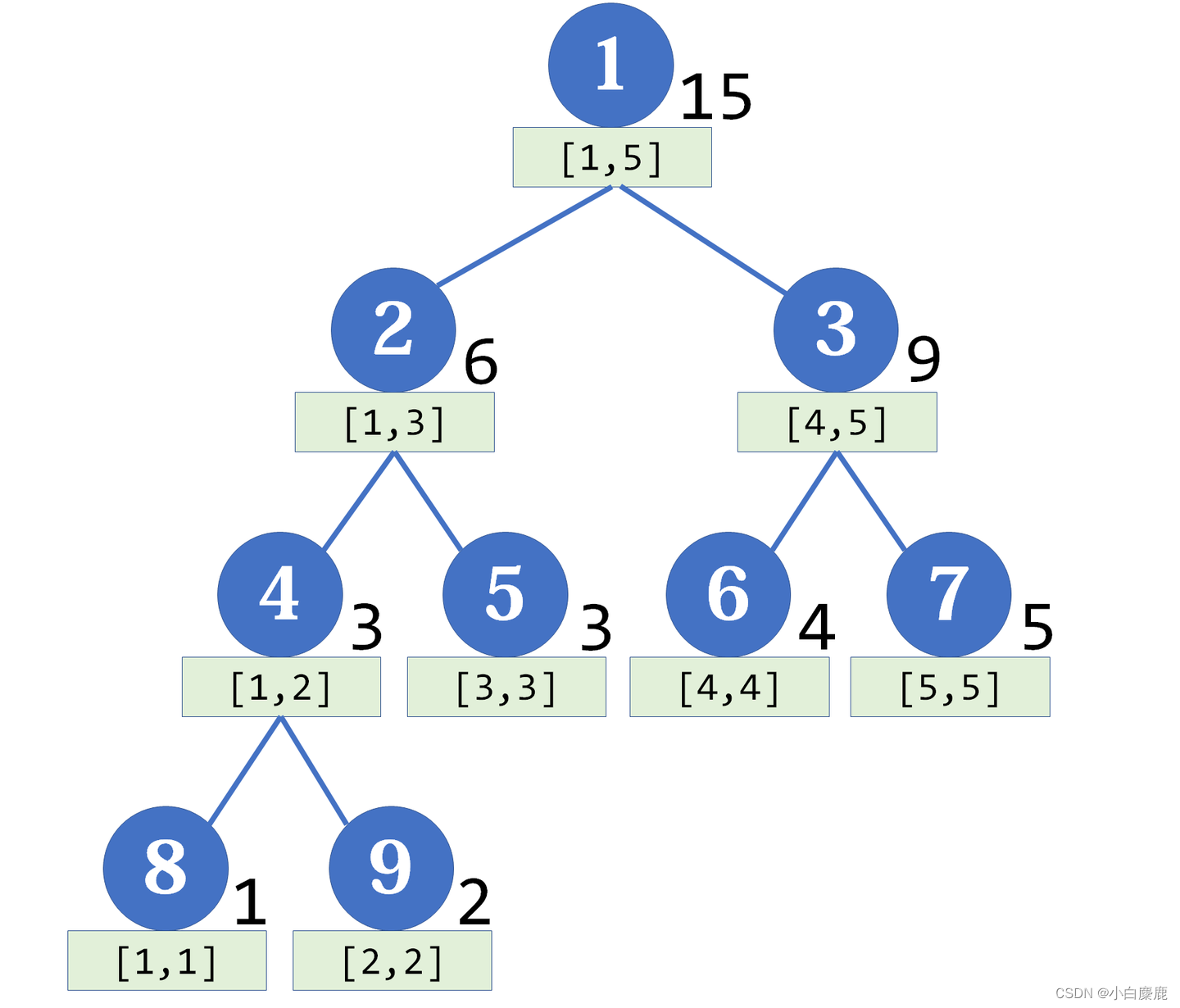
线段树的存储

通过上图不难发现，线段树是一种完全二叉树。因为我们对线段树的区间进行拆分的时候，是一个类似二分的折半拆分，将节点的区间均分成两段，分别对应其左右孩子，直至节点的左右区间相等。

所以在实现线段树时，我们一般选择用数组实现，并舍弃数组下标的0位置以1开头。这是因为如果根节点序号为1，那么对于任意一个节点序号n，那么其对应左子树的序号就为2n，右子树的序号为2n+1。我们在线段树的操作中一般就是通过数组2n和2n+1的数组下标访问节点的左右孩子的。

值得注意的是，线段树的每一个节点都表示的是一个区间范围，叶子节点也不例外，只不过叶子节点的左右区间相等，所以可以看作就是一个点。所以通常线段树的结构中都会有一个left和一个right用来表示维护的区间范围。

需要4n大小的数组

对于一个区间范围为1到n的线段树，我们一般将线段树的数组大小设置为4n。

这是因为线段树中的每个节点都表示一个区间。如果线段树是一棵完全二叉树，那么它的节点数会恰好是2n-1个（区间范围是1-n，表示最终的叶子节点有n个，那么总结点数就是2n-1）。但如果不是完全二叉树，那么总节点数目就是大于n小于等于2n-1的。又因为数组是一种线性连续的存储结构（即下标是连续的），所以为了通过2n+1这种方式来索引，就需要再为每一个叶子节点分别添加左右孩子节点，即还需再添加2n个节点（n个叶子节点，每个节点添加两个孩子节点，共添加2n个节点）。

所以最后需要的总节点数为：完全二叉树的情况需要2n-1个；非完全二叉树的情况需要大于3n小于等于4n-1个。所以为了保险起见我们取一个最安全的4n为数组大小。

线段树的区间是确定的

线段树的区间在建树时是确定的，一旦建立就不会改变。但是线段树中节点对应的区间可以随着查询或者修改操作的需要而动态变化。

所以通常情况下，线段树不支持删除操作。因为删除一个元素需要更新该元素所属的所有区间的信息，这个过程会比较复杂，而且还需要维护大量的信息。如果必须要删除某个元素，一种简单的思路是将其标记为“删除”，然后在查询时忽略这些“删除”的元素。

更普遍的情况是，对于线段树中的每个节点，我们都会记录一个标志位，表示这个节点所代表的区间是否有效或已删除。这个标志位可以放在线段树节点中对应的元素上，或者另外维护一个与线段树节点对应的标志数组。在查询或更新时，我们可以根据区间有效性进行判断，忽略已删除的区间。

线段树的难点在于lazy操作

设大L、R为为操作区间，小l、r为线段树的当前节点区间。如果要对[L,R]范围内的的数进行操作，首先判需要断当前节点所代表的区间与待修改区间之间的关系。如果这两个区间没有重叠部分，那么不需要对该节点进行修改操作，直接退出即可。如果存在重叠部分，则需要递归地访问该节点的左右子树，并将修改操作应用于相应的节点。在递归返回过程中，需要将子树的修改结果合并到当前节点。

我们以add操作为例，假设要将区间为1-n的线段树中[L,R]范围的数同时加上一个val，那么操作的大致思路是：

      如果[L,R]完全包含当前节点的[l,r]，那么就直接将当前节点的lazy值设为val，同时将当前节点的值加上val*(r-l+1) —— r-l+1为当前节点的孩子数量。

      如果[L,R]包含但并不是全包含[l,r]，那么就进行如下操作：

1、下放当前节点lazy值到左右孩子（pushdown操作）

2、判断[L,R]区间与左右孩子区间的关系，决定是否有必要进入左孩子或者右孩子。

      如果 L <= mid，说明[L,R]区间与左孩子的区间有交集，那么进入左孩子；同理，如果R >= mid+1，那么就进入右孩子。

如果[L,R]与[l,r]区间并无交集，那么就什么都不需要做。

最后，进行节点汇总（pushup操作）

而对于修改（change）等操作也是换汤不换药，大体过程类似，只不过修改操作是将所有add操作的lazy值清空，change操作的lazy值改为要修改的值（这是两个lazy值，实现时是不同的变量名）。具体的实现可以看下面的代码部分。

但需要注意的是对于pushdown方法的书写要先下放change的lazy值再下放add的lazy值。这是因为change操作会抹去add的lazy值，所以如果change的lazy值和add的lazy值同时存在，那一定是先进行了change操作之后又进行的add操作。

代码样例

#include<stdio.h> 
#include<stdlib.h>
#include<string.h>
#include<stdbool.h>
#include<assert.h>


#define MAXN 9 //注意，0位置弃掉不用，所以默认数组的有效区间为[1，MAXN-1]
//线段树结构
typedef struct
{
	struct
	{
		int l, r;		//l-r表示当前节点代表的区间 
		int sum;		//存放区间l-r范围内元素的和 
		int lazy;		//存放区间l-r范围内的lazy值 
		int change;		//存放区间l-r范围内的更新值 
		bool updata;	//存放区间l-r范围updata标志 
	//开辟数组的大小为4n
	}SNode[MAXN << 2]; 	
}SegTree; 
//更新tree树中下标为rt的节点的sum
void PushUp(SegTree* tree, int rt) 
{
	//rt位置的sum更新为 2*rt(左孩子) 与 2*rt+1(右孩子) 位置的sum之和
	(*tree).SNode[rt].sum = (*tree).SNode[rt << 1].sum + (*tree).SNode[rt << 1 | 1].sum;
	/* PS：<< 比 * 运算要快一些 */ 
}
//tree树中的rt节点的lazy/change下放
void PushDown(SegTree* tree, int rt)
{
	int l = (*tree).SNode[rt].l, r = (*tree).SNode[rt].r, mid = l + (r - l) / 2;
	//change下放
	bool changeTag = (*tree).SNode[rt].updata;
	int changeVal = (*tree).SNode[rt].change;
	if (changeTag)
	{
		//下放change
		(*tree).SNode[rt << 1].updata = true;
		(*tree).SNode[rt << 1].change = changeVal;
		(*tree).SNode[rt << 1 | 1].updata = true;
		(*tree).SNode[rt << 1 | 1].change = changeVal;
		//清除lazy
		(*tree).SNode[rt << 1].lazy = 0;
		(*tree).SNode[rt << 1 | 1].lazy = 0;
		//更新sum
		int ln = mid - l + 1, rn = r - mid;
		(*tree).SNode[rt << 1].sum = ln * changeVal;
		(*tree).SNode[rt << 1 | 1].sum = rn * changeVal;
		//最后，重置rt节点的change标志
		(*tree).SNode[rt].updata = false;
	}
	//lazy下放
	int lazyTag = (*tree).SNode[rt].lazy;
	if (lazyTag)
	{
		int l = (*tree).SNode[rt].l, r = (*tree).SNode[rt].r, mid = l + (r - l) / 2;
		//下放lazy
		(*tree).SNode[rt << 1].lazy += (*tree).SNode[rt].lazy; 
		(*tree).SNode[rt << 1 | 1].lazy += (*tree).SNode[rt].lazy; 
		//更新sum
		int ln = mid - l + 1, rn = r - mid; 
		(*tree).SNode[rt << 1].sum += ln * lazyTag;
		(*tree).SNode[rt << 1 | 1].sum += rn * lazyTag;
		//最后，清空rt节点的lazy
		(*tree).SNode[rt].lazy = 0;
	}
}
//建树，根据arr数组填充(初始化)tree的sum信息
void Bulid(SegTree* tree, int* arr, int l, int r, int rt) 
{
/* 参数说明：
	tree表示要操作的线段树，将arr数组中的内容填充到tree中
	l, r表示当前节点在arr数组的区间映射
	rt表示当前根节点的编号(下标) 
*/
	//暴力检查
	assert(tree != NULL);
	assert(arr != NULL);
	assert(l > 0);
	assert(r < MAXN);
	assert(rt > 0 && rt < MAXN << 2);
	//不论什么情况，先填充tree的l和r
	(*tree).SNode[rt].l = l;
	(*tree).SNode[rt].r = r;
	//l==r时，表示走到了可以表示一个点的区间位置，其l/r就是对应arr数组的下标，rt就是我们线段树的节点下标
	if (l == r)
	{
		(*tree).SNode[rt].sum = arr[l];
		return;
	}
	//如果当前区间不是一个点，则分别再对两个孩子节点Build
	int mid = l + (r - l) / 2; //mid是两个孩子节点的分界点
	Bulid(tree, arr, l, mid, rt << 1);
	Bulid(tree, arr, mid + 1, r, rt << 1 | 1);
	//最后不要忘了更新当前rt节点的数据(即sum的值)
	PushUp(tree, rt);
}
//区间增加，将tree树的[L,R]区间的内容增时加C
void Add(SegTree* tree, int L, int R, int C, int rt) //L,R表示操作区间，rt表示根节点的编号(下标)
{
	//暴力检查
	assert(tree != NULL);
	assert(L > 0);
	assert(R < MAXN);
	assert(rt > 0 && rt < MAXN << 2);
	//[L,R]完全包含[l,r]时，当前rt节点直接lazy增加
	int l = (*tree).SNode[rt].l, r = (*tree).SNode[rt].r; 
	if (L <= l && R >= r)
	{
		(*tree).SNode[rt].lazy += C; 
		(*tree).SNode[rt].sum += (r - l + 1) * C; 
		return;
	}
	//rt位置lazy/change下放
	PushDown(tree, rt);
	//根据左右孩子的[l,r]是否与[L,R]有交集，选择是否进行“任务下发”
	int mid = l + (r - l) / 2;
	if (L <= mid)
		Add(tree, L, R, C, rt << 1);
	if (R >= mid + 1)
		Add(tree, L, R, C, rt << 1 | 1);
	//最后，更新rt节点元素
	PushUp(tree, rt);
}
//区间更新，将tree树的[L,R]区间的内容更新为C
void Updata(SegTree* tree, int L, int R, int C, int rt) //L,R表示操作区间，rt表示根节点的编号(下标)
{
	//暴力检查
	assert(tree != NULL);
	assert(L > 0);
	assert(R < MAXN);
	assert(rt > 0 && rt < MAXN << 2);
	//[L,R]完全包含[l,r]时，当前rt节点直接updata更新
	int l = (*tree).SNode[rt].l, r = (*tree).SNode[rt].r;
	if (L <= l && R >= r)
	{
		(*tree).SNode[rt].updata = true; //当前节点标志为已更新
		(*tree).SNode[rt].change = C;    //更新值设为C
		(*tree).SNode[rt].lazy = 0;      //将之前的lazy标志清空
		(*tree).SNode[rt].sum = (r - l + 1) * C; //更新sum值
		return;
	}
	//rt位置lazy/change下放
	PushDown(tree, rt);
	//根据左右孩子的[L,R]是否与[L,R]有交集，选择是否进行“任务下发”
	int mid = l + (r - l) / 2;
	if (L <= mid)
		Updata(tree, L, R, C, rt << 1);
	if (R >= mid + 1)
		Updata(tree, L, R, C, rt << 1 | 1);
	//最后，更新rt节点元素
	PushUp(tree, rt);

}
//区间查询，查询[L,R]区间的sum值
int QuerySum(const SegTree* tree, int L, int R, int rt)//L,R表示操作区间，rt表示根节点的编号(下标) 
{
	int ans = 0;
	//暴力检查
	assert(tree != NULL);
	assert(L > 0);
	assert(R < MAXN);
	assert(rt > 0 && rt < MAXN << 2);
	//[L,R]完全包含[l,r]时，当前rt节点直接lazy增加
	int l = (*tree).SNode[rt].l, r = (*tree).SNode[rt].r;
	if (L <= l && R >= r)
	{	
		return (*tree).SNode[rt].sum;
	}
	//rt位置lazy/change下放
	PushDown(tree, rt);
	//根据左右孩子的[l,r]是否与[L,R]有交集，选择是否进行“任务下发”
	int mid = l + (r - l) / 2;
	if (L <= mid)
		ans += QuerySum(tree, L, R, rt << 1); 
	if (R >= mid + 1)
		ans += QuerySum(tree, L, R, rt << 1 | 1); 
	//最后，更新rt节点元素
	return ans; 
}

//测试用例
void test01()
{
	SegTree tree;
	memset(&tree, 0, sizeof(SegTree));
	tree.SNode[2].sum = 5;
	tree.SNode[3].sum = 8;
	PushUp(&tree, 1);
	printf("%d\n", tree.SNode[1].sum);
}
void test02()
{ 
	SegTree tree;
	memset(&tree, 0, sizeof(SegTree)); 
	int arr[MAXN] = { 0,1,2,3,4,5,6,7,8 };
	Bulid(&tree, arr, 1, MAXN - 1, 1); //rt是tree的下标
	Add(&tree, 1, 8, 1, 1);  
	Add(&tree, 2, 6, 1, 1);  
	printf("%d\n", tree.SNode[1].sum);
	int tmp; 
}
void test03()
{
	SegTree tree;
	memset(&tree, 0, sizeof(SegTree));
	int arr[MAXN] = { 0,1,2,3,4,5,6,7,8 };
	Bulid(&tree, arr, 1, MAXN - 1, 1); //rt是tree的下标
	//Add(&tree, 1, 8, 1, 1);
	//Add(&tree, 2, 6, 1, 1);
	Updata(&tree, 2, 6, 1, 1); 
	//Add(&tree, 1, 8, 1, 1);
	Add(&tree, 2, 6, 1, 1);
	printf("%d\n", tree.SNode[1].sum);
	int test_query = QuerySum(&tree, 3, 7, 1); 
	printf("%d\n", test_query);
	int tmp;
}

//主函数
int main()
{
	test01();
	test02();
	test03();
	return 0;
}