基于海鸥算法优化的核极限学习机(KELM)分类算法
文章目录
- 基于海鸥算法优化的核极限学习机(KELM)分类算法
- 1.KELM理论基础
- 2.分类问题
- 3.基于海鸥算法优化的KELM
- 4.测试结果
- 5.Matlab代码
摘要:本文利用海鸥算法对核极限学习机(KELM)进行优化,并用于分类
1.KELM理论基础
核极限学习机(Kernel Based Extreme Learning Machine,KELM)是基于极限学习机(Extreme Learning Machine,ELM)并结合核函数所提出的改进算法,KELM 能够在保留 ELM 优点的基础上提高模型的预测性能。
ELM 是一种单隐含层前馈神经网络,其学习目标函数F(x) 可用矩阵表示为:
F
(
x
)
=
h
(
x
)
×
β
=
H
×
β
=
L
(9)
F(x)=h(x)\times \beta=H\times\beta=L \tag{9}
F(x)=h(x)×β=H×β=L(9)
式中:
x
x
x 为输入向量,
h
(
x
)
h(x)
h(x)、
H
H
H 为隐层节点输出,
β
β
β 为输出权重,
L
L
L 为期望输出。
将网络训练变为线性系统求解的问题,
β
\beta
β根据
β
=
H
∗
⋅
L
β=H * ·L
β=H∗⋅L 确定,其中,
H
∗
H^*
H∗ 为
H
H
H 的广义逆矩阵。为增强神经网络的稳定性,引入正则化系数
C
C
C 和单位矩阵
I
I
I,则输出权值的最小二乘解为
β
=
H
T
(
H
H
T
+
I
c
)
−
1
L
(10)
\beta = H^T(HH^T+\frac{I}{c})^{-1}L\tag{10}
β=HT(HHT+cI)−1L(10)
引入核函数到 ELM 中,核矩阵为:
Ω
E
L
M
=
H
H
T
=
h
(
x
i
)
h
(
x
j
)
=
K
(
x
i
,
x
j
)
(11)
\Omega_{ELM}=HH^T=h(x_i)h(x_j)=K(x_i,x_j)\tag{11}
ΩELM=HHT=h(xi)h(xj)=K(xi,xj)(11)
式中:
x
i
x_i
xi ,
x
j
x_j
xj 为试验输入向量,则可将式(9)表达为:
F
(
x
)
=
[
K
(
x
,
x
1
)
;
.
.
.
;
K
(
x
,
x
n
)
]
(
I
C
+
Ω
E
L
M
)
−
1
L
(12)
F(x)=[K(x,x_1);...;K(x,x_n)](\frac{I}{C}+\Omega_{ELM})^{-1}L \tag{12}
F(x)=[K(x,x1);...;K(x,xn)](CI+ΩELM)−1L(12)
式中:
(
x
1
,
x
2
,
…
,
x
n
)
(x_1 , x_2 , …, x_n )
(x1,x2,…,xn) 为给定训练样本,
n
n
n 为样本数量.
K
(
)
K()
K()为核函数。
2.分类问题
本文对乳腺肿瘤数据进行分类。采用随机法产生训练集和测试集,其中训练集包含 500 个样本,测试集包含 69 个样本 。
3.基于海鸥算法优化的KELM
海鸥算法的具体原理参考博客:https://blog.csdn.net/u011835903/article/details/107535864
由前文可知,本文利用海鸥算法对正则化系数 C 和核函数参数 S 进行优化。适应度函数设计为训练集与测试集的错误率。
f
i
t
n
e
s
s
=
a
r
g
m
i
n
(
T
r
a
i
n
E
r
r
o
r
R
a
t
e
+
T
e
s
t
E
r
r
o
r
R
a
t
e
)
。
fitness = argmin(TrainErrorRate + TestErrorRate)。
fitness=argmin(TrainErrorRate+TestErrorRate)。
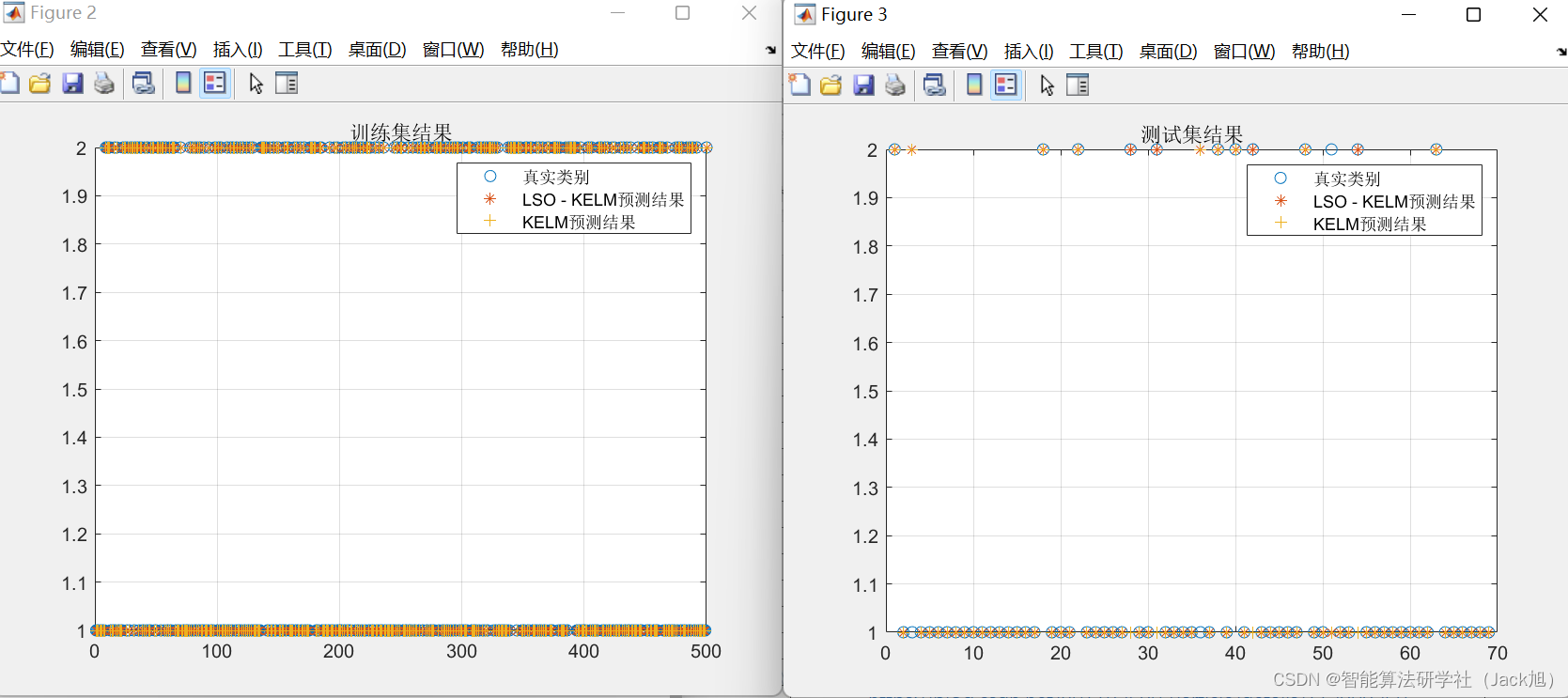
4.测试结果
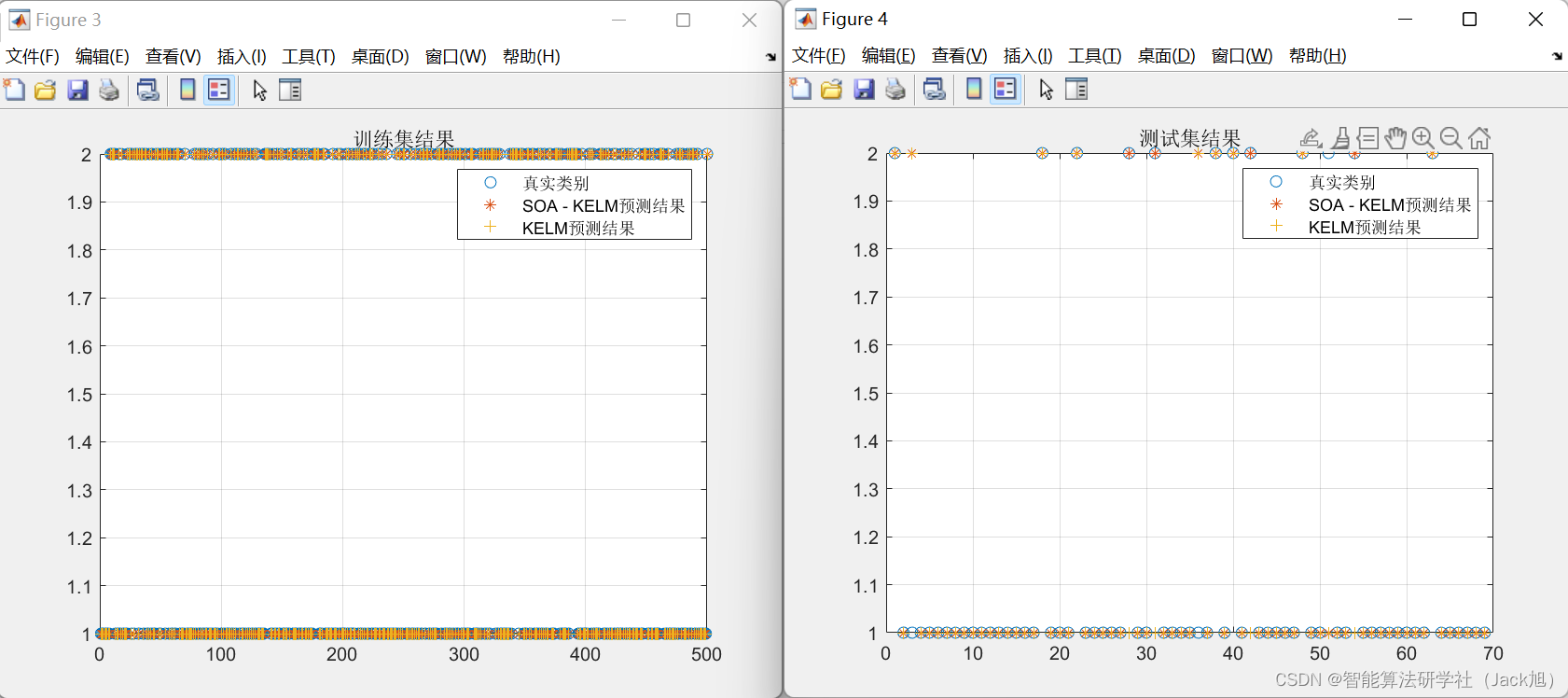
训练集SOA-KELM正确率:1
测试集SOA-KELM正确率:0.95652
病例总数:569 良性:357 恶性:212
训练集病例总数:500 良性:300 恶性:200
测试集病例总数:69 良性:57 恶性:12
良性乳腺肿瘤确诊:55 误诊:2 确诊率p1=96.4912%
恶性乳腺肿瘤确诊:11 误诊:1 确诊率p2=91.6667%
训练集KELM正确率:1
测试集KELM正确率:0.89855
病例总数:569 良性:357 恶性:212
训练集病例总数:500 良性:300 恶性:200
测试集病例总数:69 良性:57 恶性:12
良性乳腺肿瘤确诊:55 误诊:2 确诊率p1=96.4912%
恶性乳腺肿瘤确诊:7 误诊:5 确诊率p2=58.3333%
从结果可以看出,海鸥-KELM明显优于原始KELM算法