背包九讲（dp问题详解）

一、01背包问题

首先了解一下题目：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

实现思路如下：

首先我们的思路就是使用已经“已经处理的物品数”作为dp的阶段，以“背包中已经放入的物品总体积”作为附加维度
创建一个二维数组表示当前的状态（f[][]），举一个例子：f[i][j]表示只看前i个物品，总体积是j（表示剩余可以使用的体积）的情况下，总价值最大是多少。

最后的结果就是从f[n][0~v]中选取一个最大值，代码如下：
result=max(f[n][0~v]);

这里我们首先要知道的是当前的状态由之前的状态进行决定，每一次对第i件物品进行决策，状态f[i][j]不断由之前的状态更新而来

f[i][j]：

1.不取第i个物品，f[i][j]=f[i-1][j]（此时因为背包容量是不够的，所以此时的最优解就是前i-1个物品的最优解）

2.（if j>=v[i]）选择第i个物品，此时f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);（此时背包的容量是足够的，所以需要抉择是否选择第i个物品来达到最大值）

最后的答案就是1与2的最大值！

初始化：
f[0][0]=0;

初始代码：

for(int i=1;i<=n;i++)
{
    for(int j=0;j<=m;j++)
    {
      f[i][j]=f[i-1][j];
      for(int j=v[i];j<=m;j++)
      { 
         f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
      }
    }
}

通过dp的转移状态，我们发现，每一个阶段i的状态只与上一个阶段i-1的状态有关，在这种情况下，我们可以使用叫做滚动数组的优化方法，降低空间开销。

for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
           f[1&i][j]=f[(i-1)&1][j];
           for(int j=v[i];j<=m;j++)
           {
               f[i&1][j]=max(f[i&1][j],f[(i-1)&1][j-v[i]]+w[i]);
           }
        }
    }

上述程序中，我们将阶段i的状态存储在下标为i&1的二维数组中。当i为奇数时，i&1等于1，当i为偶数时，i&1为0，因此，dp的状态就相当于在f[0][]与f[1][]这两个数组中交替转移，空间复杂度从o(nm)降低为o(m)

对应代码实现如下：(这是一种较为好理解的做法，这里作为补充)

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int f[N][N];
int w[N],v[N];
int main()
{
    cin >> n >>m;
    for(int i=1;i<=n;i++)
    {
        cin >>v[i] >> w[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i-1][j];//此时对应的就是不选择的情况
            if(j >=v[i])//只有剩余的体积大于第i个物品的体积时才可以选择
            f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);
        }
    }
    int res=0;
    for(int i=0;i<=m;i++)
    {
        res=max(res,f[n][i]);
    }
    cout << res << endl;
    
    return 0;
}

优化方案：
观察上面所写的朴素做法，我们发现每一个阶段开始的时候，实际上执行了一次从f[i-1][]到f[i][]的拷贝。这提示我们其实是可以省略掉f数组的第一维，只使用一维数组，即当外层循环到第i个物品时，f[j]表示背包放入物品的最大价值和，具体代码实现如下：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int f[N];
int w[N],v[N];
int main()
{
    cin >> n >>m;
    for(int i=1;i<=n;i++)
    {
        cin >>v[i] >> w[i];
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)//倒序排序
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    int res=0;
    for(int i=0;i<=m;i++)
    {
        res=max(res,f[i]);
    }
    cout << res << endl;
    
    return 0;
}

如果各位细心观察的话，会发现我们使用了倒序排序，循环到j的时候：
（1）f数组的后半部分f[j~m]表示处于“第i个阶段”，也就是已经考虑过放入第i个物品的情况

（2）前半部分f[0~j-1]处于“第i-1个阶段”，也就是还没有第i个物品更新

接下来j会不断地减小，也就是我们不断地使用“第i-1个阶段”的状态向“第i个状态”进行转移，符合线性dp的原则（这里我对这里做一个自己的理解，其实当我们使用二维状态的时候，此时我们每添加一个物品，体积就会相应的减少（注：j表示的背包剩余的体积），所以对应的一维的时候，此时我们的体积应该也是不断地减小的，所以这里我们要使用倒序模拟体积不断减小的过程）

错误情况：（从始至终记住我们利用大的体积更新小的体积的状态）

如果我们使用了正序的话，假设f[j](f[i-1][j])是被f[j-v[i]]+w[i](f[i-1][j-v[i]])所更新的话，接下来j增加到j+v[i]时，f[j+v[i]]的状态有可能被f[j]+w[i]更新，此时二者都是处于“第i个状态”的，状态之间发生了转移，违背了线性dp的原则，相当于第i个物品被使用了两次，所以，在上述代码中必须使用倒序循环，才符合0/1背包的原则。

写一道例题巩固一下（题源来自于Acwing——278.数字组合）

题目叙述如下：
给定 N 个正整数 A1,A2,…,AN，从中选出若干个数，使它们的和为 M，求有多少种选择方案。

代码实现如下：

#include<iostream>
#include<cstring>
using namespace std;
const int N=110,M=100010;
int n,m;
int f[M];
int a[N];
int main()
{
    cin >> n >> m;
    for(int i=1;i<=n;i++)
    {
        cin>> a[i];
    }
    f[0]=1;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=a[i];j--)
        {
            f[j]+=f[j-a[i]];
        }
    }
    cout << f[m] << endl;
}

二、完全背包问题

题目描述：

有 N 种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

这道题与01背包的差别就在于01背包每件物品只有使用与不使用两种情况，但是对于完全背包问题的话每一件物品都是可以无限使用的

先来考虑使用传统的二维线性dp的做法。设f[i][j]表示从前i个物品中选出了只能总体积为j的物品放入背包，物品的最大价值：
f[i][j](1)尚未选择第i种物品f[i-1][j]

(2)从第i物品中选一个f[i][j-v[i]]+w[i]

状态转移的代码就是对应的01背包循环条件反过来即可，代码如下：

for(int j=v[i];j<=m;j++)
{
  f[j]=max(f[j],f[j-v[i]]+w[i]);
}

但是这是为什么呢？
首先我们看一下一般情况，一般大部分想到的都是枚举一下选举的次数，代码实现如下：

for(int j=m;j>=v[i];j--)
{
  for(int k=0;k*v[i]<=j;k++)
  {
    f[j]=max(f[j-k*v[i]]+k*w[i]);
  }
}

这里我们阐述优化的思路：

f[i][j]=max(f[i-1][j],f[i-1][j-v]+w[i],f[i-1][j-2*v[i]]-2*w[i]...)

f[i]][j-v]=max( f[i-1][j-v],f[i-1][j-2*v]+w[i]...)

有以上两个式子，可以得到递推公式为：

f[i][j]=max(f[i,j-v]+w , f[i-1][j])

具体代码实现如下：

#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int f[N][N];
int v[N],w[N];
int main()
{
    cin >> n>> m;
    for(int i=1;i<=n;i++) cin>> v[i] >> w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
           f[i][j]=f[i-1][j];
           if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout << f[n][m] << endl;
}

这里与0/1背包类似我们可以省略f数组中i这一维度，根据我们在0/1背包中对循环顺序的分析，当采用正序循环时，就对应每一种物品可以使用无限次（即可以容忍重叠的情况，不会的看0/1背包包正序错误的原因），也对应这f[i][j]=f[i][j-v[i]]+w[i]这个在两个均处于i阶段的状态之间转移的方程

例题巩固一下：
eg1:（题源来自Acwing——279.自然数拆分）
给定一个自然数 N，要求把 N拆分成若干个正整数相加的形式，参与加法运算的数可以重复。

代码实现如下：

#include<iostream>
#include<cstring>
using namespace std;
const int N=4010;
int f[N];
int n;
int main()
{
    cin >> n;
    f[0]=1;
    for(int i=1;i<=n;i++)
    {
       for(int j=i;j<=n;j++)
       {
          f[j]=(f[j]+f[j-i])%2147483648u;
       }
    }
    cout << (f[n]>0?f[n]-1:21474836) << endl;
    return 0;
}

三、多重背包问题

首先还是看一下题目：（题源来自Acwing.4）

有 N种物品和一个容量是 V 的背包。

第 i 种物品最多有 si 件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

实现思路：
多重背包相对于完全背包只是多了一个条件限制（即每一种物品的数量是有限的），所有我们使用朴素一些的写法就是这样子的：

#include<iostream>
using namespace std;
const int N=110;
int n,m;
int v[N],w[N],s[N];
int f[N][N];
int main()
{
    cin >> n>> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i] >> s[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=s[i]&&k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-k*v[i]]+w[i]*k);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

优化的思路：
（1）二进制优化思路：

我们知道，从 $2^0,2^1,2^2,.....,2^(k-1)$ 这k个2的整数幂中选出若干个相加，可以表示从0~2^k-1之间的任何整数.进一步的，我们求出满足 $2^0+2^1+......+2^p<=Ci$ 的最大整数p，设 $Ri=ci-2^0-2^1-.....-2^p$ （RI表示的就是剩余进行填补的那一个数，因为有可能我们利用2^0,2^1,2^2,....是没办法刚刚好表述出那一个数的），哪么：
1、根据p的最大性，有 $2^0+2^1+2^2+.....+2^(p+1)>ci$ ,可以推出 $2^(p+1)$ > $Ri$ ，因此2^0,2^1,2^2,.....,2^p选出若干个相加可以表示0~Ri之间的任何整数

2、从 $2^0,2^1,2^2,.....,2^p$ 以及 $Ri$ 中选出若干个数想加，可以表示 $Ri->Ri+2^(p+1)-1$ 之间的任何整数，而根据Ri的定义，Ri+2^(p+1)-1=Ci，因此从2^0，2^1，……，2^p，Ri中选出若干数相加表示出Ri~Ci之间的任何整数

综上所述，我们可以吧数量为Ci的第i件物品拆成p+2个物品，他们的体积分别是：
2^0*Vi,2^1*Vi,......,2^p*Vi,Ri*Vi

这p+2件物品可以凑成0~Ci*Vi之间所有可以被Vi整出的数字，并且不能凑成大于Ci*Vi的数。这等价与原问题中体积为Vi的物品可以使用0~Ci次。该方法仅把每件物品拆成O(logCi)个，效率较高。

代码实现如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=25000,M=2010;
int n,m;
int v[N],w[N];
int f[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    int cnt=0;//表示新的物品对应的编号
    for(int i=1;i<=n;i++) 
    {
        int a,b,s;//体积、价值、个数
        cin >> a>> b>> s;
        int k=1;
        while(k<=s)//把k个物品打包在一起
        {
            cnt++;
            v[cnt]=a*k;//对应的体积就是k个单个体积组织在一起
            w[cnt]=b*k;//对应的价值就是k个单个价值组织在一起
            s-=k;
            k*=2;
        }
        if(s>0)//对应的就是剩余的这一组
        {
            cnt++;//首先还是对应的编号++
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    n=cnt;//打包之后对应的数量就是我们变得组数
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout << f[m] << endl;
    return 0;
}

（2）单调队列优化（滑动窗口）

在写此题之前我们先了解一下滑动窗口：题源来自Acwing.154.滑动窗口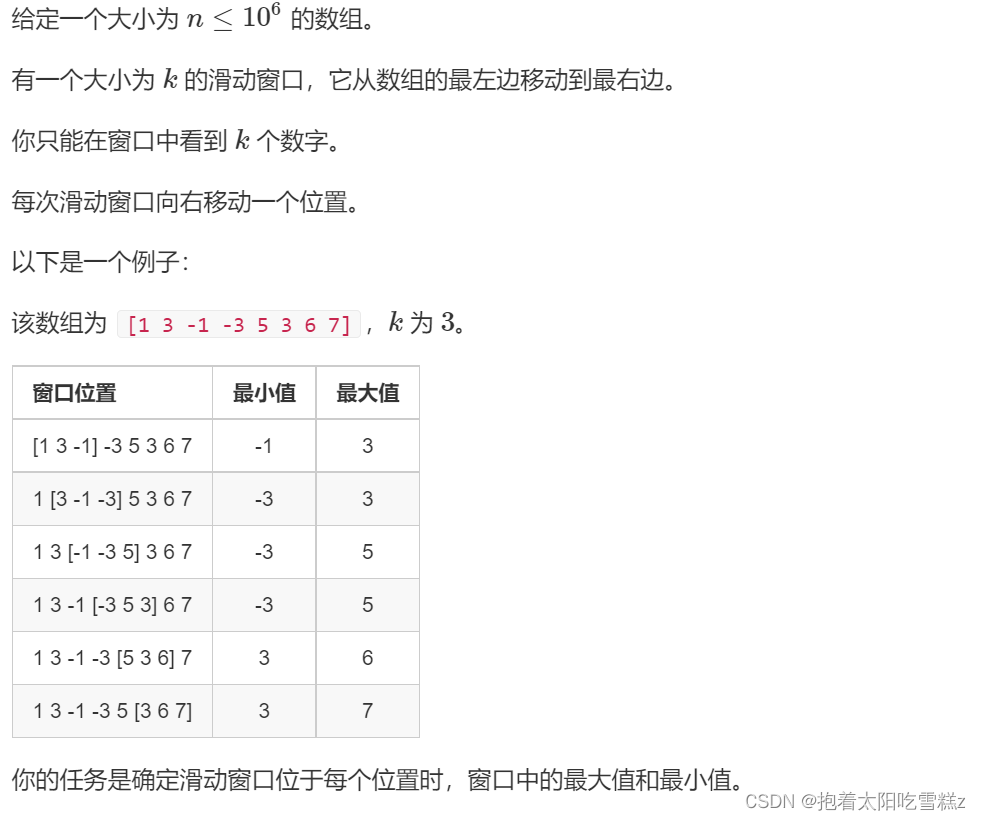

代码实现如下：

#include<iostream>
using namespace std;
const int N=1e6+10;
int a[N],n,k;
int list[N],hh,tt=-1;//队列中存储的是每一个滑动窗口中没有被剔除的数字的下标
int main()
{
    cin >> n >> k;//k是滑动窗口的长度
    for(int i=0;i<n;i++) cin >>a[i];
    for(int i=0;i<n;i++)//i是当前枚举的右端点
    {
        //判断队头是否已经滑出窗口
        if(hh<=tt && i-k+1>list[hh]) hh++;//此时就是说队头已经滑出窗口了
        while(hh<=tt && a[list[tt]]>=a[i]) tt--;//新插入的数比队尾小的话队尾就没有用了
        list[++tt]=i;//接着就是把当前数插入到队列中去
        if(i>=k-1) cout <<a[list[hh]] << ' ';
    }
    cout <<endl;
    hh=0,tt=-1;
    for(int i=0;i<n;i++)
    {
        if(hh<=tt && i-k+1 >list[hh]) hh++;
        while(hh<=tt && a[list[tt]]<=a[i]) tt--;
        list[++tt]=i;
        if(i>=k-1) cout <<a[list[hh]] << ' ';
    }
    return 0;
}

首先我们拿完全背包与多重背包的公式进行对比：

完全背包：
$f[i,j]=max(f[i-1][j],f[i-1][j-v]+w,f[i-1][j-2v]+2w,f[i-1][j-3v]+3w,....,f[i-1][j-sv])+sw$

多重背包：
$f[i,j]=max(f[i-1][j-v],f[i-1][j-2v]+w,f[j-1][j-3v]+2w,.....,f[i-1][j-sv]+(s-1)w,f[i-1][j-(s+1)v]+sw)$

这里我们发现下面是比上面多一项，我们这里是不可以使用像完全背包那样进行优化的,但是这里

因为我们发现如果使用多重背包问题的优化思路的话，最后还是会多出一项的，这就使我们无法达到优化的效果，但是我们可以先将对应的公式继续列下去，直到背包体积不可以再被使用为止。

$f[i,j]=max(f[i-1][j],f[i-1][j-v]+w,...,f[i-1][j-sv]+sw)$

$f[i,j-v]=max(f[i-1][j-v],f[i-1][j-2v]+w,...,f[i-1][j-(s+1)v]+sw)$

$f[i][j-2v]=max(f[i-1][j-2v],f[i-1][j-3v]+w,...,f[i-1][j-(s+2)v]-sw)$

$.....$

$f[i][r+sv]=max(f[i-1][r+sv],f[i-1][r+(s-1)v]+w,...,f[i-1][r]+sw)$

$f[i][r+(s-1)v]=max(f[i-1][r+(s-1)v],...,f[i-1][r]+(s-1)w)$

r=j mod vi，可以理解为是完全背包把当前物品选到不可以选之后，剩下的余数

代码实现如下：

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=20010;
int n,m;
int f[N],q[N],g[N];//q数组存储的是队头和队尾的下标
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n>>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin >> v >> w>> s;
        memcpy(g,f,sizeof  f);
        for(int j=0;j<v;j++)
        {
            int hh=0,tt=-1;
            for(int k=j;k<=m;k+=v)
            {
                if(hh<=tt && q[hh]<k-s*v) hh++;//判断队头元素是否已经滑出窗口
                if(hh<=tt) f[k]=max(f[k],g[q[hh]]+(k-q[hh])/v*w);//如果队列不是空的话，我们就求出滑动窗口的最大值
                while(hh<=tt && g[q[tt]]-(q[tt]-j)/v*w<=g[k]-(k-j)/v*w) tt--;
                q[++tt]=k;
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

四、混合背包问题

混合背包其实就是我们1~3的结合，这里我们用一道题来对它进行了解

有 N种物品和一个容量是 V 的背包。

物品一共有三类：

第一类物品只能用1次（01背包）；
第二类物品可以用无限次（完全背包）；
第三类物品最多只能用 si 次（多重背包）；

每种体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

具体的思路直接看代码，代码实现如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1010;
int n,m;
int f[N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >>m;
    for(int i=0;i<n;i++)
    {
        int v,w,s;
        cin >> v >> w >> s;//体积、价值、个数
        if(s==0)//完全背包
        {
           for(int j=v;j<=m;j++) f[j]=max(f[j],f[j-v]+w);
        }
        else
        {
            if(s==-1)
            {
                s=1;//这里我们将01背包问题转化为特殊的完全背包问题
            }
            for(int k=1;k<=s;k*=2)
            {
                for(int j=m;j>=k*v;j--)
                {
                    f[j]=max(f[j],f[j-k*v]+k*w);
                }
                s-=k;
            }
            if(s)
            {
               for(int j=m;j>=s*v;j--)
               {
                   f[j]=max(f[j],f[j-s*v]+s*w);
               }
            }
        }
    }
    cout <<f[m] <<endl;
    return 0;
}

五、二维费用的背包问题

实现思路如下：

状态表示：f[i][j][k]

（1）集合：只从前i个物品中选，总体积不超过j，总重量不超过k的方案集合

（2）属性：max

状态计算：（1）如果不选，最大的价值就是前i-1个物品的最大价值，即f[i-1][j][k]

（2）如果选了，哪么最大的价值就是f][i-1][j-vi][k-mi]+w

状态转移方程：
f[j][k]=max(f[j][k],f[j-vi][k-mi]+w);

代码实现如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n,V,M;
int f[N][N];
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> V>> M;
    for(int i=0;i<n;i++)
    {
        int v,m,w;
        cin >> v >> m >>w;
        for(int j=V;j>=v;j--)
        {
            for(int k=M;k>=m;k--)
            {
                f[j][k]=max(f[j][k],f[j-v][k-m]+w);
            }
        }
    }
    cout << f[V][M] << endl;
    return 0;
}

六、分组背包问题

实现思路：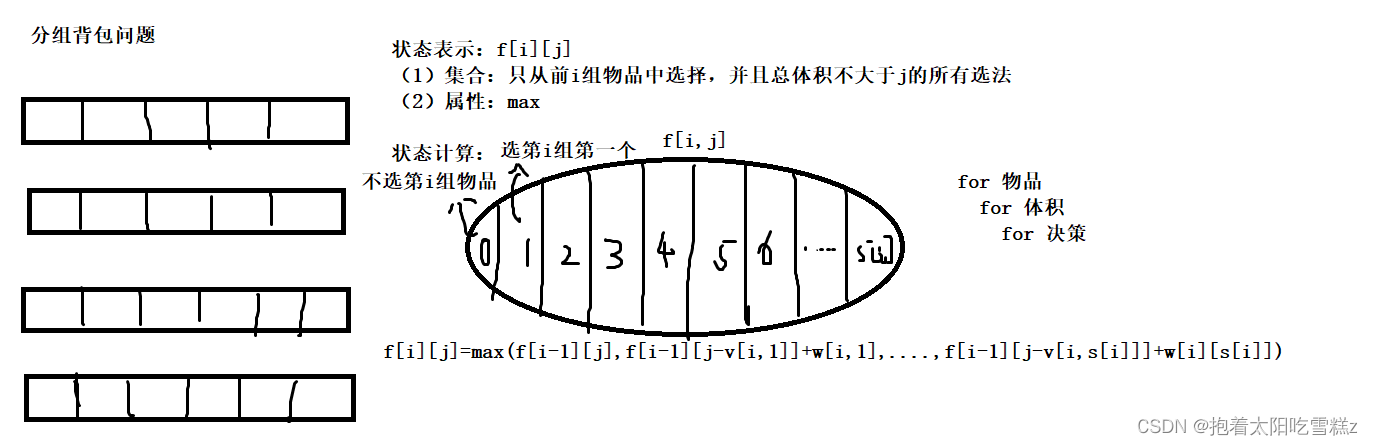

代码实现如下：

#include<iostream>
#include<algorithm>
using namespace std;
const int N=110;
int n,m;
int w[N][N],v[N][N],s[N];//s存储的是每一组的物品个数
int f[N];
int main()
{
    cin >> n >> m;
    for(int i=1;i<=n;i++)
    {
        cin >> s[i];
        for(int j=0;j<s[i];j++)
        {
            cin >>v[i][j]>>w[i][j];
        }
    }
    for(int i=1;i<=n;i++)//个数
    {
        for(int j=m;j>=0;j--)//体积
        {
            for(int k=0;k<s[i];k++)//决策
            {
                if(v[i][k]<=j)
                {
                    f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

七、背包问题求方案数

题目描述如下：

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最优选法的方案数。注意答案可能很大，请输出答案模 10^9+7 的结果。

代码实现如下：

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=1010,mod=1e9+7;
int n,m;
int f[N],g[N];//f存储的是体积恰好是j的方案数，g存储的是方案
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cin >> n >> m;
    memset(f,-0x3f,sizeof f);
    f[0]=0;
    g[0]=1;
    for(int i=0;i<n;i++)
    {
        int v,w;
        cin >> v >> w;
        for(int j=m;j>=v;j--)
        {
            int maxv=max(f[j],f[j-v]+w);
            int cnt=0;//计算一下方案数
            if(maxv==f[j]) cnt+=g[j];//如果此时与不选第i个物品的方案相同，就加上对应的方案
            if(maxv==f[j-v]+w) cnt+=g[j-v];//同理加上选择第i个物品的方案
            g[j]=cnt%mod;//存储对应的方案
            f[j]=maxv;//此时记得要将对应的最大值赋值给f[j]
        }
    }
    int res=0;
    for(int i=0;i<=m;i++)
    {
        res=max(res,f[i]);
    }//求出对应方案中的最大值
    int cnt=0;
    for(int i=0;i<=m;i++)
    {
        if(res==f[i])//如果此时方案与最大值方案是相同的，cnt就++，表示方案数+1
        {
            cnt=(cnt+g[i])%mod;
        }
    }
    cout << cnt << endl;
    return 0;
}

八、求背包问题的方案

题目描述：

有 N件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。

实现思路：
题目要求输出字典序最小的解，假设存在一个第1个物品的最优解，为了保证字典序最小哪么我们必然要选择第一个。哪么问题就转化为从2~N这些物品中找到最优解。之前的f(i,j)记录的都是前i个物品总容量为j的最优解，哪么我们现在将f(i,j)定义为第i个元素到最后一个元素总容量为j的最优解。接下来考虑状态转移：
$f(i,j)=max(f(i+1,j),f(i+1,j-v[i])+w[i])$

接下来有两种情况：
（1）不选择第i个物品，哪么最优解等同于从第i+1个物品到最后一个物品总容量为j的最优解

（2）选择第i个物品，哪么最优解等于当前物品的价值w[i]加上第i+1个物品到最后一个元素总容量为j-v[i]的最优解

计算完状态表示后，考虑如何得到最小字典序的解，首先f[1][m]肯定是最大价值，哪么我们便开始考虑是否选择第1个物品：
如果f[1][m]=f[2][m-v1]+w[1]，说明选取第1个物品可以得到最优解

如果f[1][m]=f[2][m]，说明不选取第1个物品才能得到最优解

如果f[1][m]=f[2][m]=f[2][m-v1]+w[1]，说明此时选不选都可以得到最优解，但是考虑到字典序最小，我们需要选择这个物品

代码实现如下：

#include<iostream>
using namespace std;
const int N=1010;
int n,m;
int f[N][N];
int v[N],w[N];
int main()
{
    cin >> n >> m;
    for(int i=1;i<=n;i++) cin >> v[i] >> w[i];
    //从后往前推理
    for(int i=n;i>=1;i--)
    {
        for(int j=0;j<=m;j++)
        {
            f[i][j]=f[i+1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i+1][j-v[i]]+w[i]);
        }
    }
    //f[1][m]是最大价值，表示的就是从1到最后一个物品，容量是m的最优解
    int j=m;
    for(int i=1;i<=n;i++)//遍历每一个物品
    {
        if(j>=v[i] && f[i][j]==f[i+1][j-v[i]]+w[i])
        {
            cout << i << ' ';
            j-=v[i];
        }
        
    }
    
    return 0;
}

九、有依赖的背包问题

题目描述：

有 N个物品和一个容量是V的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

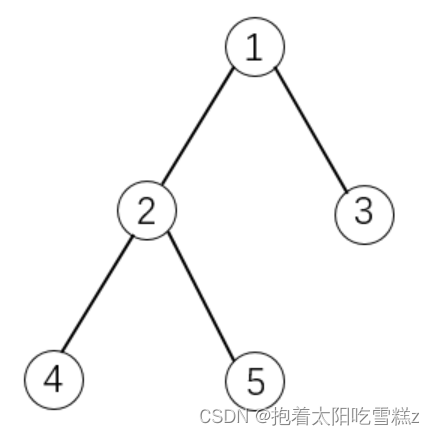
如下图所示：

如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 i，体积是 vi，价值是 wi，依赖的父节点编号是 pi。物品的下标范围是 1…N1…N。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

具体思路看以下代码：


#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 110;
int n,m;
int h[N],e[N],ne[N],idx;
int v[N],w[N],f[N][N]; 
void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;
}

void dfs(int u){
    for(int i = h[u];i!=-1;i = ne[i]){//循环物品组
        int son = e[i];//e数组的值是当前边的终点，即儿子结点 
        dfs(son); 
        for(int j = m-v[u];j>=0;j--){
        //遍历背包的容积，因为我们是要遍历其子节点，所以当前节点我们是默认选择的。
        //这个时候当前结点我们看成是分组背包中的一个组，子节点的每一种选择我们都看作是组内一种物品，所以是从大到小遍历。
        //我们每一次都默认选择当前结点，因为到最后根节点是必选的，所以要将父节点的体积先去掉 
            for(int k = 0;k<=j;k++){//去遍历子节点的组合 
                f[u][j] = max(f[u][j],f[u][j-k]+f[son][k]);
            }
        }
    }
    //因为我们之前减去了父节点的体积，所有这里要加上刚刚默认选择的父节点价值
    for(int i = m;i>=v[u];i--){
        f[u][i] = f[u][i-v[u]]+w[u];
    }
    //因为我们是从叶子结点开始往上做，所以如果背包容积不如当前物品的体积大，那就不能选择当前结点及其子节点，因此赋值为零 
    for(int i = 0;i<v[u];i++){
        f[u][i] = 0;
    }
}

int main(){
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int root;
    for(int i = 1;i<=n;i++){
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1){
            root = i;
        }else{
            add(p,i);//如果不是根节点就加入邻接表,其中p是该节点的父节点，i是当前是第几个节点
        }
    }
    dfs(root);
    cout<<f[root][m]<<endl;
    return 0;
}

十.规律总结：
（1）当空间优化为1维后，只有完全背包问题的体积是从小到大进行循环的

（2）背包问题的遍历思路：

a.第一维循环物品

b.第二维循环体积

c.第三维循环决策