1.关于模型的train/eval与batchnorm

1-1.理论

model.train()

• 启用 BatchNormalization 和 Dropout

model.eval()

• 不启用 BatchNormalization 和 Dropout.
• 框架会自动把 BN 和 DropOut 固定住，不会取平均，而是用训练好的值，不然的话，一旦test的batch_size过小，很容易就会被BN层导致生成图片颜色失真极大！
• 如果不加model.eval()，有输入数据，即使不训练，它也会改变权值。这是model中含有batch normalization层所带来的的性质（虽然看源码没看出来）。

BN详解

• BN是将每个通道进行标准化（变为标准正态分布），单位为一个batch批次的一个通道，例如若数据大小为(batch, C, W, H)则求平均后的大小为©；然后可以进行affine，即对标准化的数据进行* weight和+ bias。参考与代码：深入理解Pytorch的BatchNorm操作（含部分源码）
• 为什么要进行BN：BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布，经过BN后，大部分Activation的值落入非线性激励函数（如tanh）的线性区内，其对应的导数远离导数饱和区，这样来加速训练收敛过程。参考：整理学习之Batch Normalization（批标准化）
• 为什么有scale和shift操作（对应* weight和+ bias）：BN使得数据集中分布在了激活函数的线性部分，需要再用一个反操作来在一定程度下抵消这个线性化。参考：整理学习之Batch Normalization（批标准化）

1-2.实际运用（包含loss反向传播）

模型进行train的步骤（以毕设中face_enhance为例）：

• model.train()将BN和droupout激活，好像不一定要用，而且模型中不一定有BN
• 设置G和D的optim，包含了训练的参数，分别为G和D的参数
• model计算各种loss，并将loss分为G和D的loss
• 对G训练

g_opt.zero_grad()
gen_loss.backward()
g_opt.step()

• 对D训练和上面一样

模型进行eval的步骤

• model.eval()，好像不一定要用
• torch.no_grad()
• 没咋看了

2.CNN详解，特征图是什么

CNN处理过程

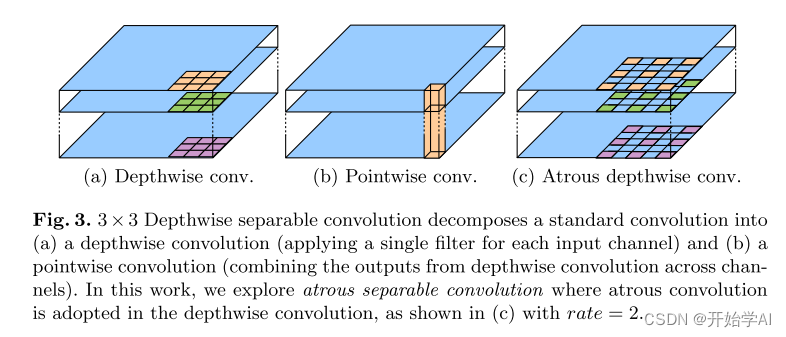
• 输入为7×7×3（意思是(7×7)×3），最后一维3表示图像颜色通道
• Filter为3×3×3（意思是(3×3)×3），那么这里的卷积核大小为3×3
• 需要注意的是输入的最后一维（3）要和Filter的最后一维（3）保持一致
• 计算方式为： 每一个对应位置相乘，最终结果相加，最后不要忘记加上偏置项
• 所以，如果前面层特征图数量为3，则每个卷积有3层，即大小为(n*n)*3
  
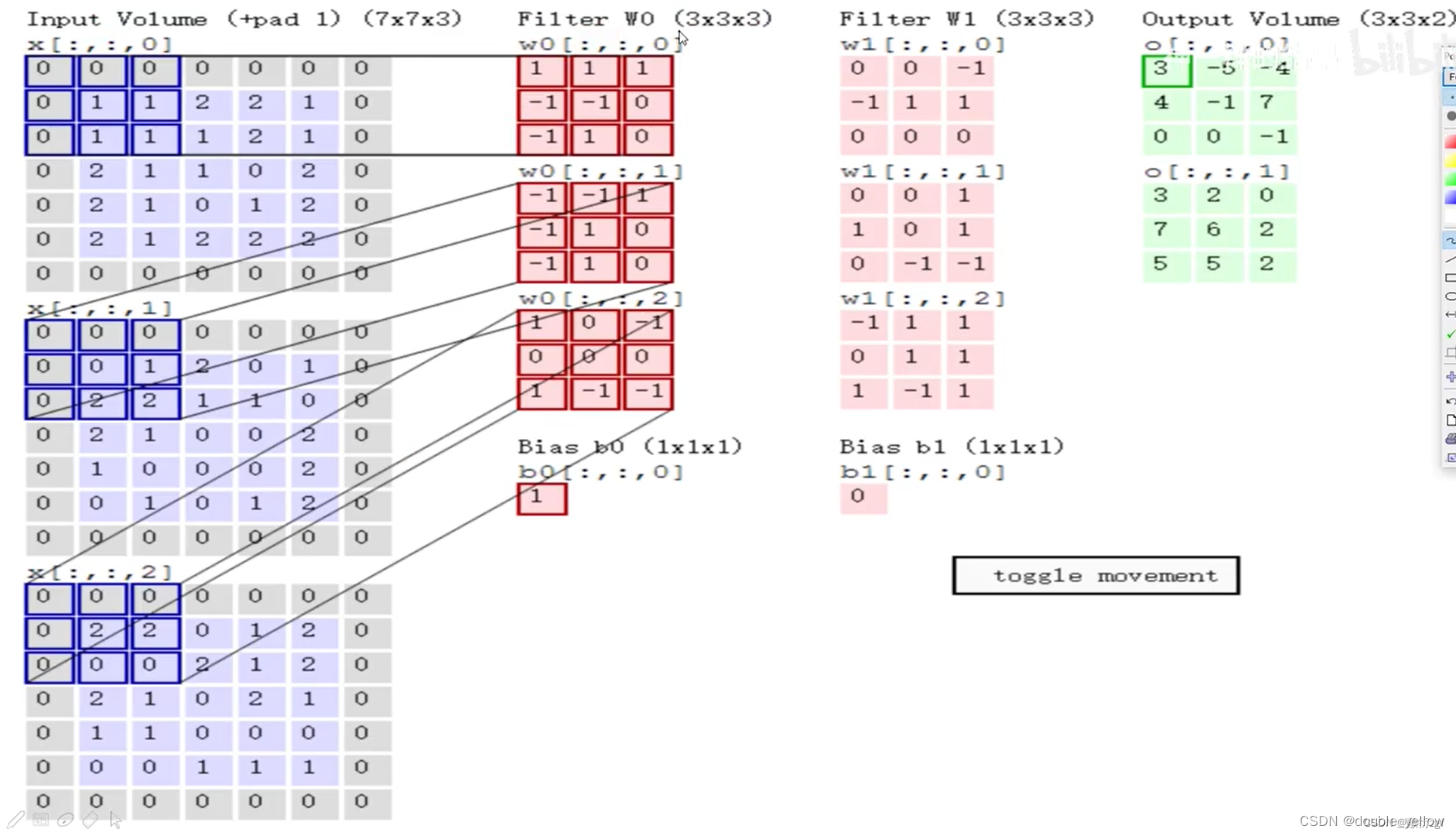
  上图来源

特征图（也叫通道）(num_features)

• 每个层中矩阵(n*n)的个数
• 比如图上输入有3个特征图，由于有2个filter所以输出为2个特征图
• 所以有多少filter就有多少特征图，比如以下VGG网络
  
  上图来源

总结（包含CNN图片的规律分析）：

• 特征图即为通道，特征图数 = 通道数 = 每一层矩阵数 = 前一层filter数，特征图数一般写在每层输出大小的第3维（如上vgg图左 224 * 224 * 64），写在convx-的后面（如图上vgg图右conv3-64），写在 @的前面（如图下8@28*28）
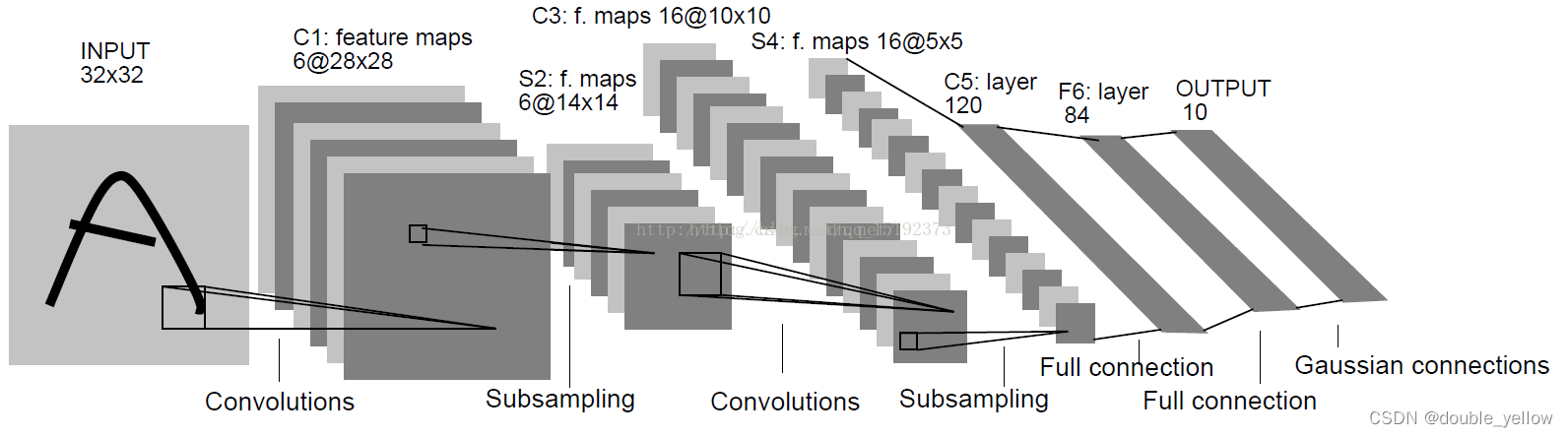
  上图来源
• 一般图中，写的都是输出的维度，而不是filter（如vgg图左224 * 224 * 64），有可能写在开头（如上图6@28*28）；一般表中，写的都是filter（如vgg图右conv3-64）。这可能是因为，图是具体例子，而表是网络结构
• pool层如果没有参数则不算在总层数内（如vgg-16中不算pool）而conv和fc有可训练参数所以算在层数内（如vgg-16中仅conv+fc有16层）
• 一个filter的参数数 = 输入/前一层特征图数 * 一个filter的大小（即n*n）+ 1个bias = 输入特征数 * (n * n) + 1；一层conv的所有filter的参数总数 = 一个filter的参数数 * 该层总filter数

3.极大似然估计与EM最大期望

• 极大似然估计是已知数据和数据分布模型，求模型参数使模型最可能出现已有结果的问题。对于不同问题使用的求参数方法不同，比如对于参数少的，只有p的模型，可以直接求导；参数多的显然不能直接求导，还有EM最大期望等方法。
• EM是迭代使用极大似然估计的方法，比如求混合高斯模型的参数时，看参考链接的方法

4.方差的n与n-1（有偏估计与无偏估计）

• n组独立同分布数据Xi相加后方差为原方差n倍，即$$Var(\sum X_i)=\sum (Var(X_i))=n{\sigma }^2$$在下面橙色的公式中用到，参考链接：独立同分布相加的方差
• 为何样本方差的无偏估计的分母为n-1，参考链接：彻底理解样本方差为何除以n-1