给你一个字符串 s，找到 s 中最长的回文子串。

如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

示例 1：

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：

输入：s = "cbbd"
输出："bb"
 

提示：

1 <= s.length <= 1000
s 仅由数字和英文字母组成

自己写的：超出时间限制了

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.length();
        string rets;
        bool flag = false;
        for(int i = 0;i<len;i++)
        {
            for (int j=0;j<len-i;j++)
            {
                int left = j;
                int right = i+j;
                while(left<=right)
                {
                    flag = true;
                    if(s[left]!=s[right])
                    {
                        flag = false;
                        break;
                    }
                    left++;
                    right--;
                }
                if(flag)
                    rets = s.substr(j, i+1);
            }
        }
        return rets;
    }
};

第二解法：

class Solution {
public:
    string longestPalindrome(string s) {

        string rets="";
        for(int i =0;i<s.length();i++)
        {
            //奇数
            int l =i-1,r=i+1;
            while(l>=0&&r<s.length()&&s[l]==s[r]) l--,r++;
            if(rets.length()<r-l-1) rets=s.substr(l+1,r-l-1);//因为l减1了，所有此处加1

            //偶数
            l=i,r=i+1;
            while(l>=0&&r<s.length()&&s[l]==s[r]) l--,r++;
            if(rets.length()<r-l-1) rets=s.substr(l+1,r-l-1);//因为l减1了，所有此处加1
        }
        return rets;
    }
};

示例模板：

Manacher算法：可以在O(n)的时间内求出一个字符串的最长回文串。

第一步：改造字符串

在字符串之间和串两端插入#，改造后，都变成奇回文串，方便统一处理。

奇回文串aba     #a#b#a#

偶回文串abba   #a#b#b#a#

s[0] = '$' 是哨兵（边界）

//改造串
scanf("%s",a+1);
int n = strlen(a+1),k=0;
s[0]='$',s[++k]='#';
for(int i=1;i<=n;i++)
    s[++k]=a[i],s[++k]='#';
n=k;

第二步：回文半径d[i]

以i为中心的最长回文串的长度的一半，叫回文半径。

i     1  2  3  4  5  6  7  8  9

s    #  a  #  a  #  b  #  a  #

d[i] 1  2  3  2  1  4  1  2  1

以b为例：b的最长回文#a#b#a#,长度为7，向上取整，回文半径为4。

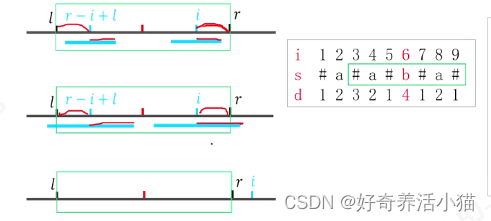
第三步：加速盒子[l,r]

算法过程中我们维护右端点最靠右的最长回文串，利用盒子，借助之前的状态来加速计算新的状态。盒内d[i]可以利用对称点的d值转移，盒外暴力。

i     1  2  3  4  5  6  7  8  9

s    #  a  #  a  #  b  #  a  #

d[i] 1  2  3  2  1  4  1  2  1

算法流程：

计算完前i-1个d的函数，维护盒子[l,r]

1.如果i<=r(在盒内），i的对称点为r-i+l;

(1)若d[r-i+l]<r-i+1(对称点回文半径还在盒内)，则d[i]=2*mid-i。

(2)若d[r-i+l] > r-i+1(对称点回文半径还在盒外)，则令d[i]=r-i，从r往后暴力枚举。

2.如果i>r(在盒外），则从i开始暴力枚举。

3.求出d[i]后，如果i+d[i]-1>r,则更新盒子l=i-d[i]+1,r=i+d[i]-1。

class Solution {
public:
    static const int N = 1010, M = 2 * N;
    char str[M];
    int ls[M];
    string manacher(string s) {
        int l = 0, r = 0, mid = 0;
        int cur = 0;
        int n = s.size();
        str[l++] = '$';
        str[l++] = '#';
        for (int i = 0; i < s.size(); ++i) {
            str[l++] = s[i];
            str[l++] = '#';
        }
        str[l] = 0;

        for (int i = 0; i < l; ++i) {
            ls[i] = r > i ? min(ls[2 * mid - i], r - i) : 1; //在盒内的处理
            while (i - ls[i] > 0 && i + ls[i] < l) //在盒外的处理
                if (str[i - ls[i]] == str[i + ls[i]])ls[i]++;
                else break;
            if (i + ls[i] > r) {
                r = i + ls[i];
                mid = i;
            }
            if (ls[i] > ls[cur])cur = i;
        }
        // cout<<str<<endl;
        // cout<<cur<<endl;
        int left = cur - ls[cur] + 1, right = cur + ls[cur] - 1;
        string res = "";
        for (int i = left; i <= right; ++i) {
            if (str[i] != '#' && str[i] != '$')res += str[i];
        }
        return res;
    }
    string longestPalindrome(string s) {
        return manacher(s);
    }
};