键树_Trie树_介绍和C语言实现

键树_Trie树形式_树介绍及C语言实现

前言

上一篇提到键树有两种不同的表示方法，它们分别是双链树和Trie树，在上文中对双链树的数据结构以及在键树上的C语言实现做了详细的分析与讨论。如若键树中的结点的度较大，则采用Trie树结构较双链结构更为合适。本文将介绍Trie树的数据结构基本特征，在此基础上，将实现Trie树的插入、删除和查找等基本操作。本文严格采用《数据结构》（严蔚敏）对Trie树的约束定义，请读者特别留意其前提条件。

Trie树介绍

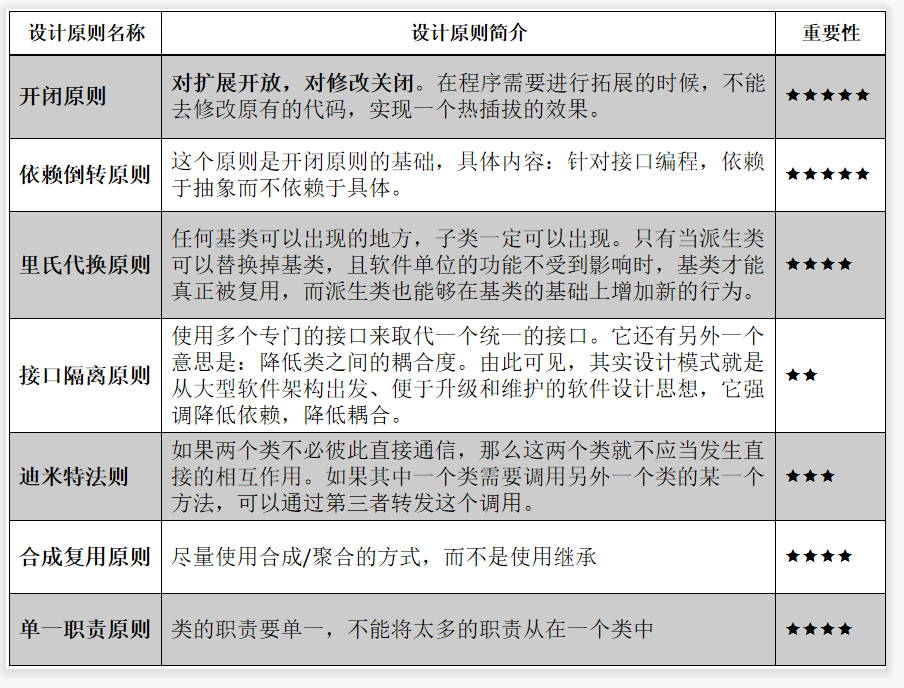
用树的多重链表来表示键树，则树的每个结点中应含有d个指针域，此时的键树就成为称作Trie树，如果结点中仅含有数字，规定d的值为11；如果结点中仅含有大写字母或小写字母，规定d的值为27，d定义为结点的最大度（子树指针数量）。

若重键树中某个结点到叶子结点的路径上的每个结点都只有一个孩子，则可将该路径上的所有结点压缩为一个“叶子结点”，且在该叶子结点储存关键字既指向记录的指针的信息等。

从结点Z到结点$单支树，相应的Trie树中就只有含有一个关键字ZHAO及相关记录信息的叶子结点。对于关键字CHEN，从结点C到结点$，结点H和E都不是单支树，但是结点N和结点$为单支树，所以μ直接指向叶子结点CHEN$。对于关键字CHA，从结点C到结点 $，每个结点都不是单支树，最后代表$字符的φ指针指向最终的叶子结点及相关的记录信息。

因此在Trie中有两种结点，分支结点和叶子结点，分支结点中含有d个指针域和一个指示该节点中非空指针域的个数的整数；叶子结点中含有关键字与指向记录的指针域。显而易见，在分支结点中，不设定数据域，每个分支结点所表示的字符均有其父节点的指针位置代表的字符决定，比如β结点所代表的的字符为根节点中β结点所在位置的字符，也就是β代表的字符为C。值得一提的是，可以采用线性哈希函数实现字符和其代表结点的对应关系，本文中采用int ord(char ch)作为哈希函数，实现字符和指针之间映射关系。

在这里插入图片描述

Trie树常见操作

3.1 查找操作

从上图中可以看出，在查找成功时走了一条从根节点到叶子结点的路径。例如在上图中查找CHEN, 从根节点出发，经过β结点，然后再到达δ结点，最后来到μ结点，μ结点指向叶子结点，叶子结点的关键字与CHEN匹配，从而判定查找成功。

如果要查找关键字CHI，类似地，从根节点出发，经过β结点，然后到达δ结点，在δ结点中，I字符指向的结点为空，从而判定结点查询失败。

3.2 插入操作

由于在特定的条件下可将路径上所有的结点压缩为一个叶子结点，这就使得插入操作显得比较复杂。插入过程中，分为两种不同的情形，从根节点出发，开始比对待插入的关键字字符代表的结点是否存在，如果指针存在，则不断往下搜索，直至指针为空或指针指向叶子结点。为了描述方便，假定新插入的关键字与现有树中的关键字都不相同。

第一类所代表为p指针为空的情形，要求在如下的子树中插入关键字CHAO, 它代表第一类插入情形，从根节点出发，关键字C代表的结点已存在，β指针代表结点C，按照前述讨论，继续往下搜索H结点，δ指针代表结点H，之后来到代表A的λ结点，在λ结点中，发现代表O的结点为空，这时候直接创建一个叶子结点，在O的位置处储存叶子结点的指针ω。

插入前：

在这里插入图片描述

插入后：

在这里插入图片描述

第二种情况，相对而言稍微复杂，p指针指向为叶子结点，具体看一个例子。在下面的Trie树中插入关键字CAKMO$。

在这里插入图片描述

首先从根节点出发，查找C对应的为β结点，在查找A对应的结点为γ结点，γ结点对应为叶子结点，此叶子结点的关键字信息为CAKMI$ , 通过比较发现，一直到M，二者的关键字字符都相同，可以理解为单树，然后分别为O和I，有两个分支结点，最后$字符相同。

通过上述阐述，不难发现，如果遇到叶子结点，在插入新节点过程中，实际上需要比较已有的叶子结点和待插入结点的关键字的相关信息，如果相同位置代表的字符相同，则直接创建分支结点，分支结点中的d为1，重复前述过程直至两个关键字当中的字符不相同，此时需要创建两个叶子结点（当然也可以选择保存原有的叶子结点，直接赋值），总结上述的过程，整个过程包括：

分支结点替换叶子结点（γ结点为分支节点,替换之前的叶子结点）
创建分支结点（ε,ζ）
创建叶子结点(η,θ)，η,θ分别代表原有叶子结点和现插入的叶子结点

完成关键字CAKMI$插入后，新Trie树结构为，

在这里插入图片描述

3.3 删除操作

删除操作与插入操作类似，首先需要找到待删除关键字所在的叶子结点，如果结点度大于2，那么直接删除此叶子结点即可。

比如要删除关键字CHAO$，直接在λ结点删除ω结点即可，删除后对整个Trie树没有任何影响。

在这里插入图片描述

如果删除关键字的度d为2，那么就要向上回退直至某个结点的度≥2为止，由于无法确定回退高度，选择采用递归删除为最佳的程序实现方式。

那么是否存在删除关键字的度d为1的情况呢？这个问题留给大家去思考。根据Trie树的定义，答案显然是否定的，如果度为1，那么就是独树，它可以向上继续压缩直至不是独树。

程序实现

根据上述描述，程序实现是水到渠成的事情，在此不再赘述。

4.1 头文件定义

/**
 * @file TrieTree.h
 * @author your name (you@domain.com)
 * @brief
 * @version 0.1
 * @date 2023-05-10
 *
 * @copyright Copyright (c) 2023
 *
 */

#ifndef TRIETREE_H
#define TRIETREE_H
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>

#define EQ(a,b) ((a)==(b))
#define LT(a,b) ((a)<(b))
#define LQ(a,b) ((a)<=(b))

#define MAXKEYLEN 16
#define N         27

typedef char KeyType;
typedef char* Record;


typedef struct  SElemType
{
    KeyType key;
    Record  value;
}SElemType;

//Dynamic Search Table
typedef struct DSTable
{
    SElemType *elem;
    int        len;
} DSTable;

void CreateTable(FILE *fp, DSTable *st);


typedef struct KeysType
{
    char ch[MAXKEYLEN];
    int num;
}KeysType;

typedef enum NodeKind
{
    LEAF,
    BRANCH
} NodeKind;

/*
typedef struct DLTNode
{
    char symbol;
    NodeKind kind;
    struct DLTNode *next;
    union 
    {
        Record infoptr;
        struct DLTNode *first;
    };
    
}DLTNode, *DLTree;

*/

typedef struct TrieNode
{
   NodeKind kind;
   //anonymous union structure
   union
   {
        struct 
        {
            KeysType keys;
            Record   infoptr;
        } lf; //leaf=lf

        struct
        {
            struct TrieNode *ptr[N];
            int              num;
        }bh; //branch=bh   
   };
   
}TrieNode, *TrieTree;

/**
 * @brief Create a trie tree object
 * 
 * @param trie Pointer to Trie tree
 */
void create_trie(TrieTree *trie);

/**
 * @brief Insert a new keys into the Trie tree
 * 
 * @param trie Trie tree
 * @param keys Keys to be inserted
 */
void insert_trie(TrieTree root, KeysType keys);


/**
 * @brief Delete the keys from the trie tree
 * 
 * @param trie Target trie tree
 * @param keys KeysType 
 */
int delete_trie(TrieTree root, KeysType *keys, int i,TrieTree *temp_node);

/**
 * @brief Search the keys from KeysType
 * 
 * @param trie Trie key type
 * @param keys To be searched keys
 * @return Record Return record if execute successfully
 */
Record search_trie(TrieTree root, KeysType keys);

int ord(char ch);

void create_leaf_node(TrieTree p, KeysType keys,int i);

void create_branch_node(TrieTree p,int i);

#endif

4.2 函数实现文件

/**
 * @file TrieTree.c
 * @author your name (you@domain.com)
 * @brief
 * @version 0.1
 * @date 2023-05-10
 *
 * @copyright Copyright (c) 2023
 *
 */
#ifndef TRIETREE_C
#define TRIETREE_C
#include "TrieTree.h"

void CreateTable(FILE *fp, DSTable *st)
{
    int n;
    char str[MAXKEYLEN];
    int i;


    n=0;
    // 当读取 (n-1) 个字符时，或者读取到换行符时，或者到达文件末尾时，它会停止，具体视情况而定。
    while (fgets(str, MAXKEYLEN, fp) != NULL)
    {
        n++;
    }

    fseek(fp,0,SEEK_SET);

    st->len=n;
    st->elem=(SElemType *)malloc(sizeof(SElemType)*(n+1));

    for(i=1;i<=n;i++)
    {
        st->elem[i].value = (Record)malloc(sizeof(char) * MAXKEYLEN);
        memset(st->elem[i].value, 0, sizeof(char) * MAXKEYLEN);
        fscanf(fp,"%c %s%*c",&(st->elem[i].key),st->elem[i].value);
    }

    return;    
}

void create_trie(TrieTree *trie)
{
    *trie=(TrieTree)malloc(sizeof(TrieNode));
    (*trie)->kind=BRANCH;
    (*trie)->bh.num=0;
    memset((*trie)->bh.ptr,0,sizeof(TrieNode *)*N);

    return;
}

void insert_trie(TrieTree root, KeysType keys)
{
    TrieTree p;
    TrieTree pre_p;

    TrieTree new_leaf_node;
    TrieTree q;
    KeysType exist_keys;

    int      i;
    int      j;

    p=root;
    pre_p=NULL;
    i=0;

    //find the insert location;
    while(p && p->kind==BRANCH && i<keys.num)
    {
        pre_p = p;
        p=p->bh.ptr[ord(keys.ch[i])];        
        i++;
    }

    i-=1;
    j = i;

    if(p&&p->kind==LEAF)
    {
        exist_keys = p->lf.keys;
        while(i<keys.num && j<exist_keys.num &&keys.ch[i]==exist_keys.ch[j])
        {

            //Execute replacement action to replace leaf with branch
            create_branch_node(pre_p, ord(keys.ch[i])); // it would be NULL at ptr[ord(keys.ch[i])]
            // pre_p will point to newly-created node(replace the old leaf with new branch)
            pre_p=pre_p->bh.ptr[ord(keys.ch[i])]; 
            
            i++;
            j++;  
        }
        // reset to zero before inserting the created leafs
        pre_p->bh.num-=1; 
        create_leaf_node(pre_p, exist_keys, j); //create the exist_keys leaf node
    }
    
    create_leaf_node(pre_p, keys, i); //create the new keys leaf node

    return;
}

//use recurision to achieve the function
int delete_trie(TrieTree root, KeysType *keys, int i, TrieTree *temp_node)
{

    int temp;
    
    if (root->kind == LEAF)
    {
        *temp_node=root;
         return 1; //continue action after stack frame pops up
    }
    else
    {
        temp=delete_trie(root->bh.ptr[ord((*keys).ch[i])],keys,i+1,temp_node);
        if(temp)
        {
            if (root->bh.ptr[ord((*keys).ch[i])] == *temp_node)
            {
                root->bh.num--;
                root->bh.ptr[ord((*keys).ch[i])] == NULL; //delete the target leaf
                if (root->bh.num == 1) // if there is still one remaining, just search it
                {
                    for (int j = 0; j < N; j++)
                    {
                        if (root->bh.ptr[j] && root->bh.ptr[j]->kind == LEAF)
                        {
                            *keys = root->bh.ptr[j]->lf.keys;
                            *temp_node = root->bh.ptr[j];
                            return 1; //search successfully and return 1
                        }
                    }
                }
               
                return 0;  // otherwise, return 0 and no actions will be taken when stack pop up
            }
            else if(root->bh.num==1) // if the immediate parent only has one pointer, continue upward search
            {
                return 1;
            }
            else //when root->bh.num>=2, the other leaf will be installed and action ended
            {
                root->bh.ptr[ord((*keys).ch[i])]=*temp_node;
                return 0;
            }
        }
        else //no actions will be taken, just return 0
        {
            return 0;
        } 
    }
}

Record search_trie(TrieTree root, KeysType keys)
{
    int i;
    TrieTree p;

    i=0;
    p=root;

    while(p && p->kind==BRANCH && i<keys.num)
    {
        p=p->bh.ptr[ord(keys.ch[i])];
        i++;
    }

    if(p && p->kind==LEAF)
    {
        return p->lf.infoptr;
    }
    else
    {
        return NULL;
    }
}

//----------------------------------//


int ord(char ch)
{
    return (ch=='$'?0:ch-'A'+1);
}

void create_leaf_node(TrieTree p, KeysType keys,int i)
{
    TrieNode * new_node;
    Record     str;

    new_node = (TrieTree)malloc(sizeof(TrieNode));
    new_node->kind = LEAF;

    str = (char *)malloc(sizeof(char) * (keys.num + 1));
    memset(str, 0, sizeof(char) * (keys.num + 1));
    strncpy(str, keys.ch, keys.num);

    new_node->lf.keys = keys;
    new_node->lf.infoptr = str;

    p->bh.ptr[ord(keys.ch[i])]=new_node;
    p->bh.num+=1;

    return;
}

void create_branch_node(TrieTree p, int i)
{
    TrieNode *new_node;

    new_node = (TrieTree)malloc(sizeof(TrieNode));
    new_node->kind = BRANCH;
    memset(new_node->bh.ptr,0,sizeof(TrieTree)*N);
    new_node->bh.num=1;

    p->bh.ptr[i] = new_node;
 
}

#endif

4.3 测试文件

/**
 * @file TrieTree_main.c
 * @author your name (you@domain.com)
 * @brief
 * @version 0.1
 * @date 2023-05-10
 *
 * @copyright Copyright (c) 2023
 *
 */
#ifndef DLTREE_MAIN_C
#define DLTREE_MAIN_C
#include "TrieTree.c"

int main(void)
{
    int i;
    int j;
    int len;
    FILE *fp;
    DSTable st;
    TrieTree root;
    TrieTree temp_node;
    KeysType keys;
    KeysType del_keys;

    fp=fopen("data.txt","r");
    CreateTable(fp,&st);

    create_trie(&root);

    for(i=1;i<=st.len;i++)
    {
        len=strlen(st.elem[i].value);
        memset(keys.ch, 0, sizeof(char) * MAXKEYLEN);
        strcpy(keys.ch,st.elem[i].value);
        keys.num=len;
        if(i==2)
        {
            del_keys=keys;
        }
        insert_trie(root,keys);
    }

    delete_trie(root,&del_keys,0,&temp_node);

    printf("Inserting is done\n");
    

    printf("\n");

    getchar();
    fclose(fp);
    return EXIT_SUCCESS;
}


#endif

4.5 数据源文件(data.txt)

1 CAI$
2 CAO$
3 CHA$
4 CHANG$
5 CHAO$
6 CHEN$
7 ZHAO$

小结

通过C语言实现Trie树，对Trie的结构有了更深入的了解，同时加深了指针在程序中的应用，通过重复操作分析，抽象出创建分支结点和叶子结点的子函数，使程序可读性增强。

参考资料：

《数据结构》严蔚敏

键树_Trie树_介绍和C语言实现_20230511

键树_Trie树形式_树介绍及C语言实现

相关文章

【软件工程】期末复习总结（通俗易懂，学不会来打我）

126-Linux_git安装及使用

Netty编程入门超级详细，有这篇就足够了

MyBatis的CRUD

算法套路十五——最长公共子序列LCS

Windows系统配置Anaconda虚拟环境，并安装Numpy、Scipy和Matplotlib等模块方法

异步电机速度估计-模型参考自适应MRAS法（补充）

Calico的BGP打通Kubernetes网络和局域网

双链表——“数据结构与算法”

浅谈 Node.js

【LLM】LangChain基础使用（构建LLM应用）

BGW协议（算数共享）

c++ 友元介绍

Vue最新快速上手教程（狂神）

【JAVA】黑马程序员JAVA教程笔记基础篇 Day 1

【2023最新】几乎涵盖你需要的Android性能优化的所有操作

【网络安全CTF】BUUCTF(Basic篇)

三极管知识大全

【刷题笔记】另类加法+走方格的方案数

网易云音乐开发--完善video模块