一、另类加法
题目:
牛客网链接:另类加法_牛客题霸_牛客网
描述
给定两个int A和B。编写一个函数返回A+B的值,但不得使用+或其他算数运算符。
测试样例:1,3
返回:4
解析:
因为无法使用算数运算符,我们需要用到其他运算方式,能够想到的可以有位运算方式。
因为是加法,我们不妨追求溯源,看看我们小时候计算加法的方式:

我们可以分解一下上面的两种操作:

此时两个结果中有一方存在零了,另一方就是结果了,否则就继续上述操作。同理,在10进制的+法我们也可以运用于2进制,那么此时位运算就可以起到作用了,我们以1 + 3为例子:

解答:
需要注意,当不进位的结果为0的时候,表示此时就是能够被2整除的(相当于十进制中能被10整除的),此时进位的结果就是结果。同理相反。
class UnusualAdd {
public:
int addAB(int A, int B) {
if (A == 0) return B;
if (B == 0) return A;
int a = A ^ B;// 直接相加不进位
int b = (A & B) << 1; // 进位数字
return addAB(a, b);
}
};二、走方格的方案数
题目:
牛客网链接:走方格的方案数_牛客题霸_牛客网
描述
请计算n*m的棋盘格子(n为横向的格子数,m为竖向的格子数)从棋盘左上角出发沿着边缘线从左上角走到右下角,总共有多少种走法,要求不能走回头路,即:只能往右和往下走,不能往左和往上走。
注:沿棋盘格之间的边缘线行走
数据范围:1≤n,m≤8
输入描述:
输入两个正整数n和m,用空格隔开。(1≤n,m≤8)
输出描述:
输出一行结果
示例1
输入:2, 2
输出:6
解析:
分析问题需要善于用逆向思维。
在一个格子内,如下4*4格子,我们想要从左上到右下总共的走法(注意限制条件,只能往右和往下走,并且沿棋盘格之间的边缘线行走)
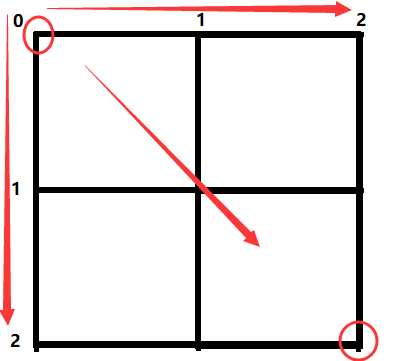
如果直接正面的去想,我们会发现会存在很多种,直接计算并且编码实现的不好实现。
但是,如果一旦反过来想,问题就很简单了。我们要求的左上到右下的走法总数,也就是(0, 0)->(2, 2);从(2, 2)开始看,到(2, 2)的走法总数不就是到(2, 1)的走法总数+到(1, 2)的走法总数吗?而(2, 1)的走法总数不就是(2, 0)的走法总数+(1, 1)的走法总数吗?依次向上,一直到最后的(0, 0)。
此时问题就很好解决了。我们可以将此问题抽象为每次就是求其左边和上面的位置走法总数相加。而最左边那一列和最右边那一列走法总是只有1种。利用此方可求解。
解答:
求解可以利用递归的思想。也可以创建二维数组,进行dp操作。
#include <iostream>
#include <vector>
using namespace std;
// 使用递归
int Func(int n, int m)
{
if (n == 0 || m == 0) return 1;
return Func(n - 1, m) + Func(n, m -1);
}
int main()
{
int n, m;
while (cin >> n >> m)
{
cout << Func(n, m) << endl;
}
return 0;
}