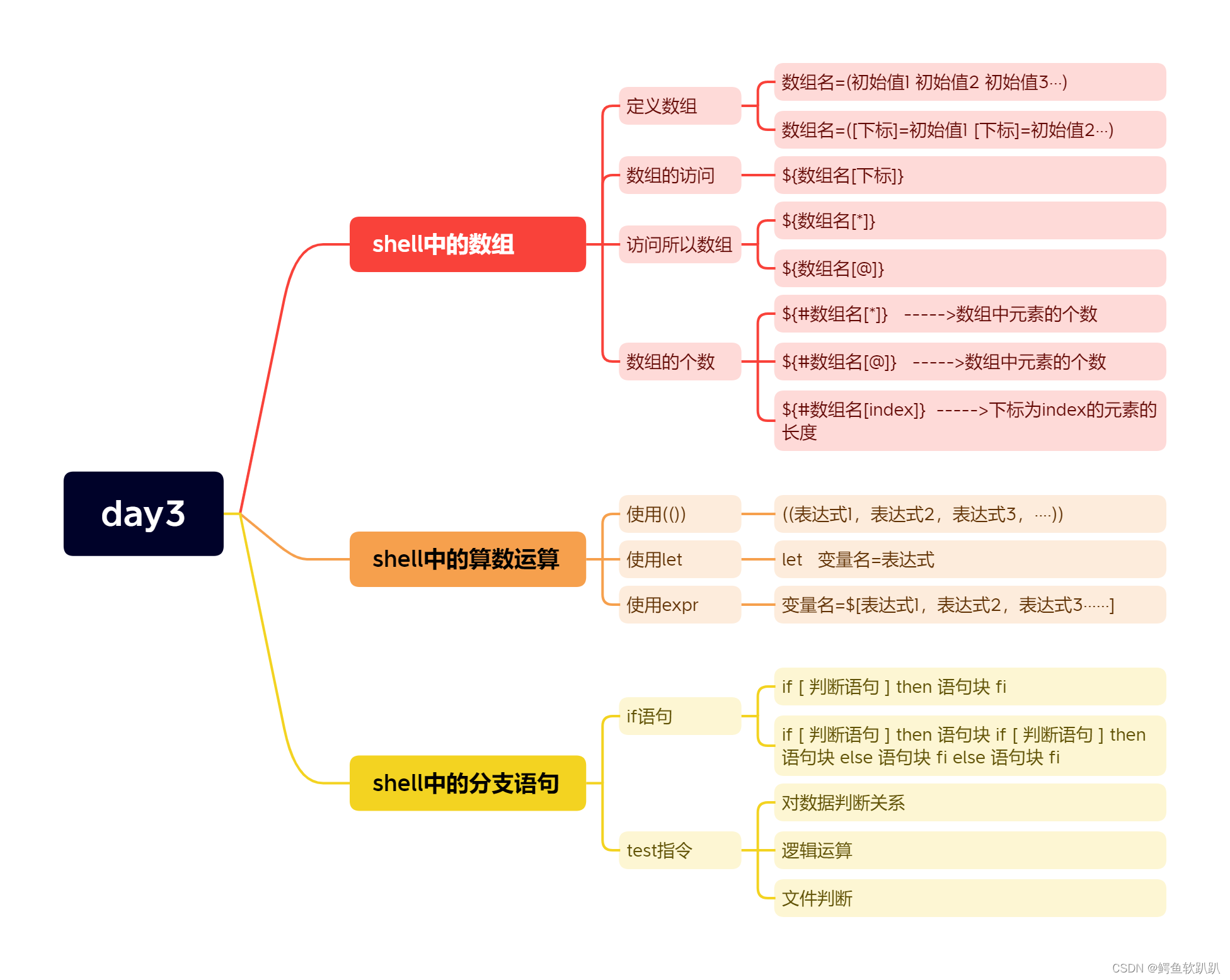
概述

BGW协议可以用于对域上包含加法、乘法、常数乘法门的算术电路求值，此协议强依赖Shamir秘密分享方案，利用其同态特性对各个秘密份额进行适当的处理，就可以在秘密值上进行安全计算。

加法门

算数加法共享（两方）

一方持有密文一方持有密钥。

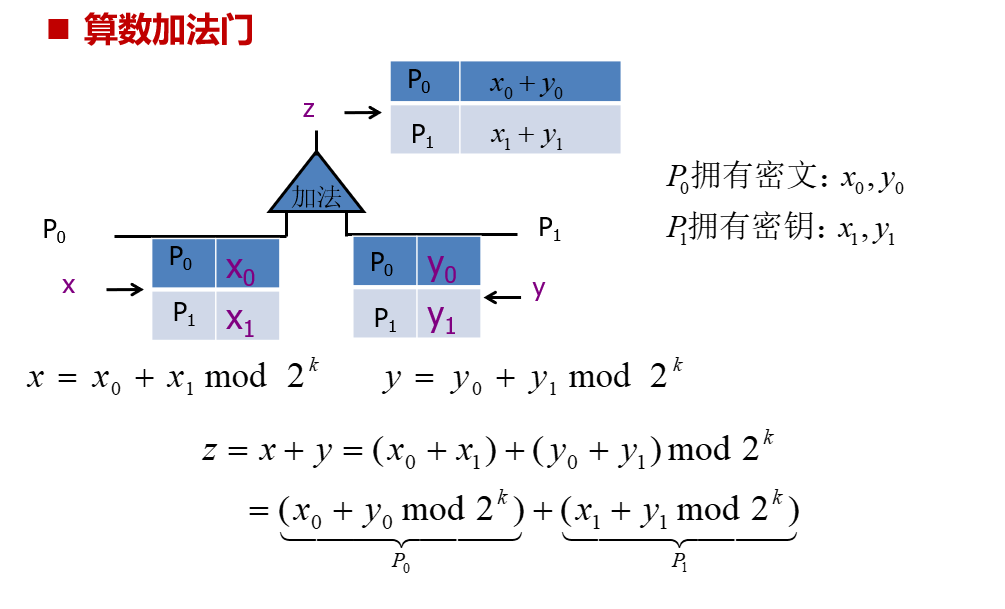
显然算数加法门完成计算结果是无需交互的，在本地即可完成计算。（GMW协议相当于mod 2 计算。）

基于Shamir方案的加法共享（多方）

考虑两个输入门$x,y$，一个输出门$z$的加法门，计算$z=y+x$。同样，为了达到共享，需要将两个输入门的输入导线值秘密拆分给多个参与方。首先对每个输入导线针对要输入的值$xory$，选择一个$t$阶的多项式，然后进行Shamir的$(t,n)$分享，将秘密份额分发给其他的参与方，这样假设有$n$个参与方，那么就会得到$n$份来自不同输入导线的秘密份额。本地求和累加，即可得到输出门$z$值的一个$(t,n)$分享。只需$t+1$个及以上联合重构秘密即可还原出最终的加法结果。

乘法门

算数乘法共享（两方）

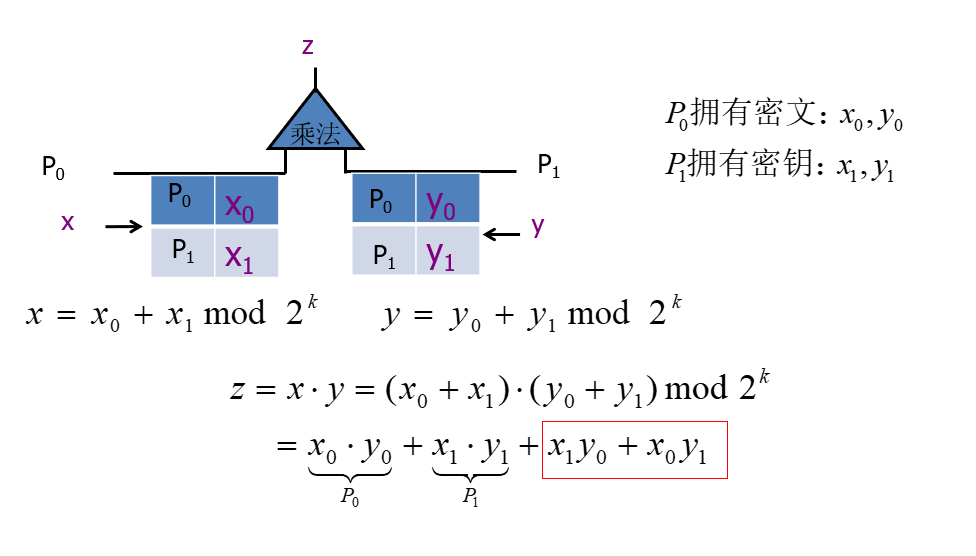
如图显然，和GMW协议一样，除了自己能够计算出来的一部分外，还会多出一部分必须要交互才能计算出来的结果。如果采用和布尔共享一样的OT协议的话，那么每个未知数据的可能情况非常多，多个组合起来就更加多。为了保障隐私，掩盖子电路的输出，所以需要添加掩码了，这里采用了乘法三元组。

Beaver三元组（乘法三元组）

一种MPC协议的构造范式：分为参与方输入未知时的预处理阶段和参与方选择好输入时的在线阶段。预处理阶段会为参与方生成一些相互之间具有一定关联性的随机量。参与方于在线阶段的时候则可以消耗这些随机量。
在前面的方法中，我们可以看到，协议中唯一的实际开销是为每个乘法门求值时的通信开销，由此这里采用三元组将大部分通信量转移到预处理阶段。
所谓乘法三元组，即$ab=c$,$a$和$b$是从域中随机选择的一个随机数，每一个乘法门求值都需要消耗掉一个三元组

步骤
依旧考虑两个输入门$x,y$，一个输出门$z$的乘法门，计算$x\ast y=z$，首先给两个输入值添加掩码，也就是把三元组的元素进行两方拆分。也就是$a=a_0+a_1,b=b_0+b_1$，让两方分别持有一部分，注意到$ab=(a_0+a_1)(b_0+b_1)=a_0{b}_0+a_0{b}_1+a_1{b}_0+a_1{b}_1$，将其拆分为两部分$(ab{)}_0$和 $(ab{)}_1$
具体操作可以调用同态加密的方法，假设选定一个同态加密算法（如Paillier）

• $P_1$计算$E(a_1),E(b_1)$然后发送给$P_0$
• $P_0$计算$E(b_1{)}^{a_0}E(a_1{)}^{b_0}E(a_0{b}_0-a_1{b}_1)=E(a_0{b}_0+a_0{b}_1+a_1{b}_0-a_1{b}_1)$发送给$P_1$
• $P_1$解密即可
• 此时$(ab{)}_0=a_1{b}_1$，而$(ab{)}_1=a_0{b}_0+a_0{b}_1+a_1{b}_0$

现在两方分别持有$x_i,y_i,a_i,b_i$。

• 让$x，y$以掩码方式$e=x+a$和$f=y+b$输出，即公开$x_i+a_i,y_i+b_i$，这样双方就能本地计算出$e,f$
• 计算得到$\begin{array}{rl}xy& =(e-a)(f-b)\\ & =ef-fa-eb+ab\end{array}$，那么将其拆分一下，得到$\begin{array}{l}(xy{)}_0=-f{a}_0-e{b}_0+(ab{)}_0\\ (xy{)}_1=ef-f{a}_1-e{b}_1+(ab{)}_1\end{array}$
• 配合上前面计算出来的$(ab{)}_0$和 $(ab{)}_1$即可在本地得到结果。

多方的乘法共享

基于Shamir秘密分发方案

=还是考虑两个输入门$x,y$，一个输出门$z$的乘法门，计算$x\ast y=z$，直观上来看，实质是两个输入门的$t$阶多项式相乘，这将得到一个阶数为$2t$的多项式，假定为$q(x)$,每个参与方的秘密份额就是这个多项式上的一个点$q(i)=[v_x][v_y]$（注意：$[]$代表$(t,n)$的Shamir秘密分享的秘密份额），显然恢复出正确的结果是需要至少$2t+1$个秘密份额，这已经超过了Shamir秘密分享方案的阈值$t$，那么如何解决阈值溢出问题呢？毫无疑问需要对乘积多项式进行降阶。
注意: 这里需要满足要求$2t+1<n$，即安全性基于多数诚实假设。
目标：获取$q(0)$的有效秘密份额，且多项式阶不超过阈值$t$，从而能够让$t+1$个人能够恢复出秘密$q(0)$。
核心思路：使用参与方的秘密份额的线性函数表示$q(0)={\sum }_{i=1}^{2t+1}{\lambda }_{i}q(i)$，这是一个$(t,n)$共享转加法$t$的一个形式，也就是将$q(0)$转换为了$2t+1$份秘密份额的和。然后参与方的编号如果自始至终都默认为$[1,\mathrm{2..2}t]$这样的增长方式的话，加上${\lambda }_i$是一个知道编号就能计算出的一个值，那么就可以在本地模拟$2t+1$个秘密份额进行求和。

具体降阶步骤如下，

1. 首先每个参与方基于自己的$q(i)$进行一次Shamir的$(t,n)$秘密共享，并将对应的秘密份额$[q(i)]$发送给其他参与方，也就是每个参与方将$q(i)$作为秘密和常数项，选择一个$t$阶多项式，分发对应子秘密份额给其他参与方。
2. 各个参与方在本地计算$[q(0)]={\sum }_{i=1}^{2t+1}{\lambda }_i[q(i)]$，$[q(0)]$表示乘积秘密值$q(0)$的有效份额，${\lambda }_i$是对应的拉格朗日系数。

此时因为$[q(i)]$是一个$(t,n)$共享，那么此时每个人计算出的$[q(0)]$也就是一个$(t,n)$共享。这就完成了降阶的操作。

基于随机输入以及三元组方案 （加法秘密分享）

每个参与方为每个乘法门构造三元组$[a][b]=[c]$（自己持有，其他参与方不知道，已知ab，c就定了），各个参与方持有秘密份额$[v_x],[v_y]$（对于每个参与方的输入导线都会随机分配一个秘密份额，只有对应参与方知道其值，同样满足$v={\sum }_{i=1}^n[v]$）想要计算$[v_x{v}_y]$
（注意：$[]$为加法分享的子秘密份额，即$a={\sum }_{i=1}^n[a],b={\sum }_{i=1}^n[b]$），计算步骤如下

1. 各个参与方在本地计算$[d]=[v_x-a]$并公开
2. 各个参与方在本地计算$[e]=[v_y-b]$并公开
3. 则有下列等式

$\begin{array}{rl}{v}_x{v}_y& =(v_x-a+a)(v_y-b+b)\\ & =(d+a)(e+b)\\ & =de+db+ae+ab\\ & =de+db+ae+c\end{array}$
$d,e$是被公开了的，而$[a],[b],[c]$各个参与方均持有，因此各个参与方均可计算秘密份额
$[v_x{v}_y]=de+d[b]+e[a]+[c]$

参考

实用安全多方计算导论
Arithmetic Sharing（算术共享）