第十四届蓝桥杯C++--A组题解（更新中）

news2024/12/24 9:03:00

本来考场上做完想着这回图一乐，打打暴力混个省奖得了，看完民间题解感觉跟自己估计的差不多，应该挺寄的，没想到出分捡了个省一，喜提弱省省一倒数
这篇博客把自己会的题先放上来，其他的题慢慢补，好多知识点都没碰到过。。、
至于为什么一个月前的比赛现在才发，是因为我突然发现洛谷上已经更新了今年的篮球杯题目了，也刚好没啥事做。。。。

[蓝桥杯 2023 省 A] 填空问题

题目描述

A. 幸运数

小蓝认为如果一个数含有偶数个数位，并且前面一半的数位之和等于后面一半的数位之和，则这个数是他的幸运数字。例如 $2314$ 是一个幸运数字，因为它有 $4$ 个数位，并且 $2 + 3 = 1 + 4$ 。现在请你帮他计算从 $1$ 至 $100000000$ 之间共有多少个不同的幸运数字。

B. 有奖问答

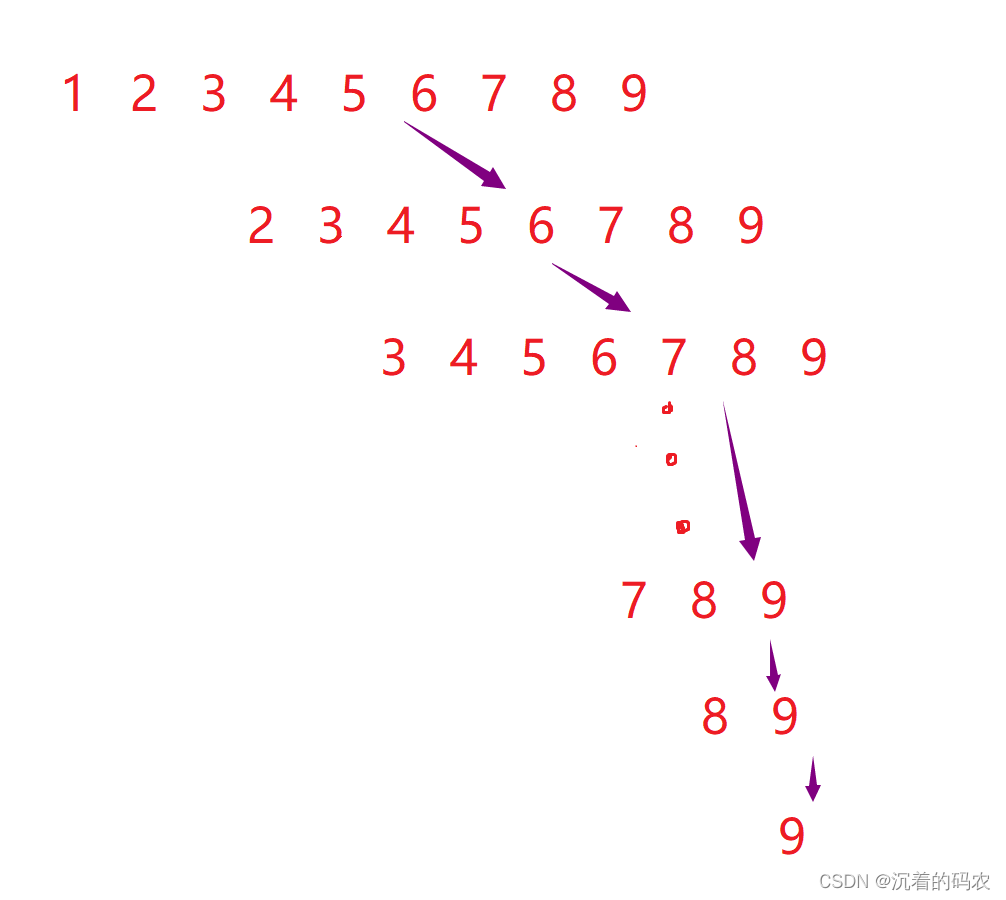
小蓝正在参与一个现场问答的节目。活动中一共有 $30$ 道题目，每题只有答对和答错两种情况，每答对一题得 $10$ 分，答错一题分数归零。

小蓝可以在任意时刻结束答题并获得目前分数对应的奖项，之后不能再答任何题目。最高奖项需要 $100$ 分，所以到达 $100$ 分时小蓝会直接停止答题。

已知小蓝最终实际获得了 $70$ 分对应的奖项，请问小蓝所有可能的答题情况有多少种？

输入格式

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

您可以通过提交答案文件的方式进行提交。你需要将你的答案放在 1.out 和 2.out 中，其中 1.out 对应 A 题的答案，2.out 对应 B 题的答案。

输入文件包含一个字符，代表题目编号（A 或 B），你需要输出对应的答案。

以下模板供参考：

#include<bits/stdc++.h>
using namespace std;

char pid;
int main() {
    cin >> pid;
    if(pid == 'A')
        puts("Answer for Problem A");
    else
        puts("Answer for Problem B");
    return 0;
}

输出格式

提示

第十四届蓝桥杯大赛软件赛省赛 C/C++ 大学 A 组 A-B

这俩填空都让我在本地用暴力做出来了，好好写个搜索是能出来的答案就不放了，要拿好成绩这两道肯定得对。。毕竟其他的更做不来了。。。

················································································································
················································································································

[蓝桥杯 2023 省 A] 平方差

题目描述

给定 $L, R$ ，问 $\leq x \leq R$ 中有多少个数 $x$ 满足存在整数 $y, z$ 使得 $x=y^2-z^2$ 。

输入格式

输入一行包含两个整数 $L, R$ ，用一个空格分隔。

输出格式

输出一行包含一个整数满足题目给定条件的 $x$ 的数量。

样例 #1

样例输入 #1

1 5

样例输出 #1

提示

【样例说明】

$1=1^2-0^2$
$3=2^2-1^2$
$4=2^2-0^2$
$5=3^2-2^2$

【评测用例规模与约定】

对于 $\%$ 的评测用例， $\leq 5000$ ；

对于所有评测用例， $\leq L \leq R \leq 10^9$ 。

第十四届蓝桥杯大赛软件赛省赛 C/C++ 大学 A 组 C

无脑打表找规律，可以非常明显的看出来mod 4 == 2的数是无解的
需要用O（1）的时间判断，找到规律以后稍微推一下也能很快出来

/*
本地打表找规律
发现只有mod 4 == 2的数无解

#include <bits/stdc++.h>
using namespace std;

bool check(int n)
{
    for(int i = 0; i <= 100; i ++) {
        for(int j = i; j <= 101; j ++) {
            if(j * j - i * i == n) return true;
        }
    }

    return false;
}
int main()
{
    for(int i = 1; i <= 100; i ++) {
        if(check(i)) cout << i << endl;
    }

    return 0;
}
*/

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
LL L, R;

int main()
{
    cin >> L >> R;
    
    LL sum = R - L + 1;
    //找到第一个和最后一个无解的数
    while(L % 4 != 2) L ++;
    while(R % 4 != 2) R --;
    
    sum -= ( (R - L) / 4 + 1);
    
    
    cout << sum;
    
    return 0;
}

[蓝桥杯 2023 省 A] 更小的数

题目描述

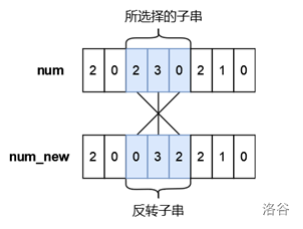
小蓝有一个长度均为 $n$ 且仅由数字字符 $\sim 9$ 组成的字符串，下标从 $0$ 到 $n - 1$ ，你可以将其视作是一个具有 $n$ 位的十进制数字 $n u m$ ，小蓝可以从 $n u m$ 中选出一段连续的子串并将子串进行反转，最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 $num_{new}$ 满足条件 $num_{new}<num$ ，请你帮他计算下一共有多少种不同的子串选择方案，只要两个子串在 $n u m$ 中的位置不完全相同我们就视作是不同的方案。

注意，我们允许前导零的存在，即数字的最高位可以是 $0$ ，这是合法的。

输入格式

输入一行包含一个长度为 $n$ 的字符串表示 $n u m$ （仅包含数字字符 $\sim 9$ ），从左至右下标依次为 $\sim n-1$ 。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例说明】

一共有 $8$ 种不同的方案：

所选择的子串下标为 $0\sim1$ ，反转后的 $num_{new} = 120102 < 210102$ ；
所选择的子串下标为 $0\sim2$ ，反转后的 $num_{new} = 012102 < 210102$ ；
所选择的子串下标为 $0\sim3$ ，反转后的 $num_{new} = 101202 < 210102$ ；
所选择的子串下标为 $0\sim4$ ，反转后的 $num_{new} = 010122 < 210102$ ；
所选择的子串下标为 $0\sim5$ ，反转后的 $num_{new} = 201012 < 210102$ ；
所选择的子串下标为 $1\sim2$ ，反转后的 $num_{new} = 201102 < 210102$ ；
所选择的子串下标为 $1\sim4$ ，反转后的 $num_{new} = 201012 < 210102$ ；
所选择的子串下标为 $3\sim4$ ，反转后的 $num_{new} = 210012 < 210102$ 。

【评测用例规模与约定】

对于 $20\%$ 的评测用例， $\le n \le 100$ ；

对于 $40\%$ 的评测用例， $\le n \le 1000$ ；

对于所有评测用例， $\le n \le 5000$ 。

考场上打的暴力，没做过区间DP，之后学了发现其实难度不高

/*
赛时只写了个暴力。
正解区间DP
if(s[i] == s[j]) f[i][j] = f[i+1][j-1]
因为从i+1转移过来
所以i要从大到小遍历
*/

#include <bits/stdc++.h>
using namespace std;

string s;
bool f[5005][5005];
int sum;

int main()
{
    cin >> s;
    
    for(int i = s.length() - 1; i >= 0; i --) {
        for(int j = i + 1; j <= s.length() - 1; j ++) {
            if(s[i] > s[j]) f[i][j] = 1;
            else if(s[i] < s[j]) f[i][j] = 0;
            else f[i][j] = f[i + 1][j - 1];

            if(f[i][j]) sum ++;
        }
    }

    cout << sum;
    
    return 0;
}