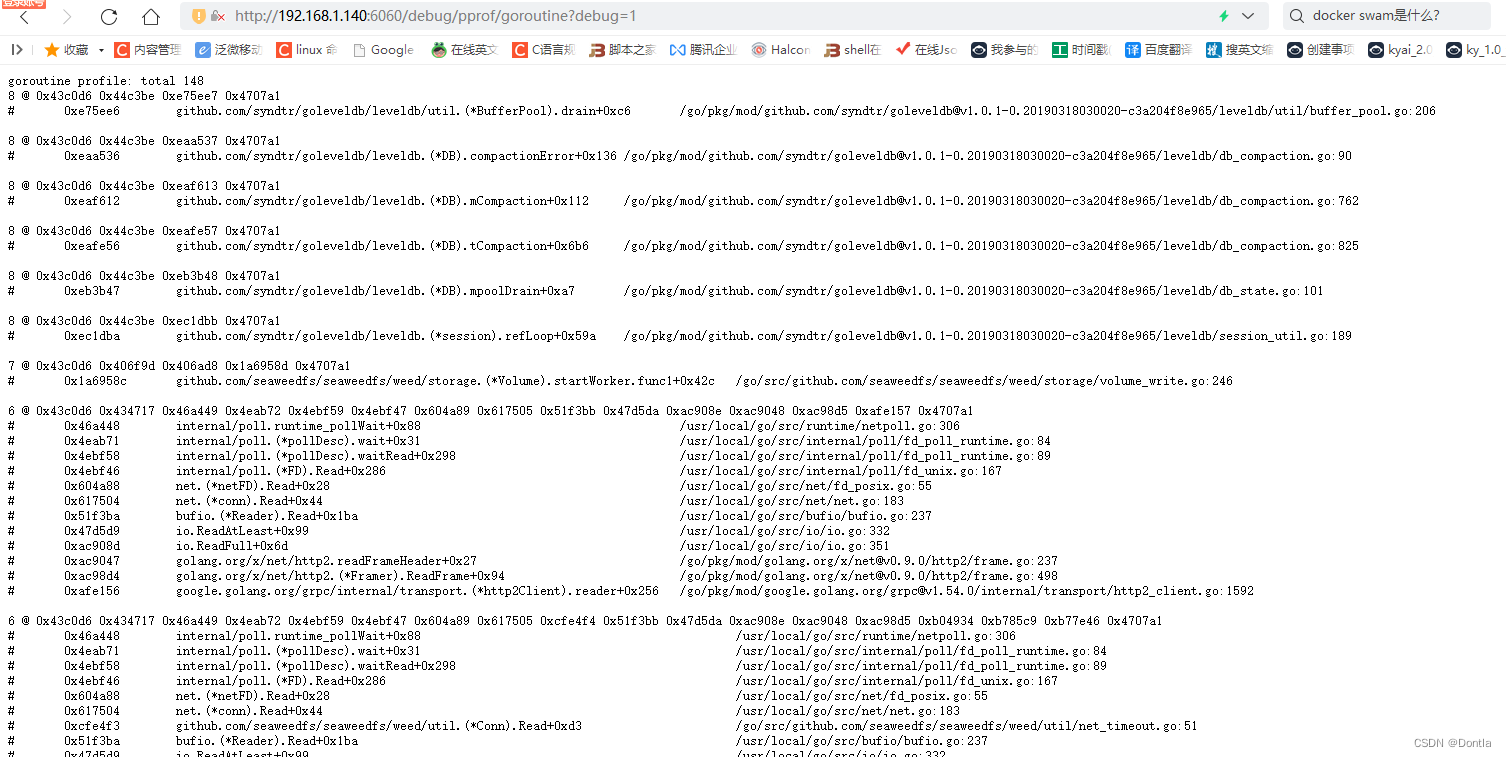
目录
任务描述
相关知识
大整数的思想
大整数加法
大整数减法
大整数与整数的乘法
大整数乘法
大整数与整数的除法
n的阶乘求解思路
编程要求
测试说明
任务描述
本关任务:掌握大整数的基本思想,并运用大整数的基本运算计算出常规整数n的阶乘,然后统计大整数n!中数字0的个数。
相关知识
为了完成本关任务,你需要掌握:1.大整数的思想,2.大整数加法,3.大整数减法,4.大整数与整数的乘法,5.大整数乘法,6.大整数与整数的除法,7.n的阶乘求解思路。
大整数的思想
大整数的思想:用数组存储大整数(超长整数),为处理简单起见约定每个数组元素存放相同位数(T位)的数字片段(假定T=4位)。
设定一个大小为N的整型数组a[0,1,..,N−1],给定一个大整数998877665544332211,每个数组单元使用T=4位存储,为了方便计算,将大整数的低位存入数组的高维索引,如下图所示:

大整数加法
大整数的加法和一般的整数加法是类似的,从低位开始,同位置的数相加,若大于进制K=10000,则进位,以此类推。特别的,当进制K=10时,每个数组单元存储的数字为T=1位,大整数的加法运算就等价于常规整数的加法运算,只不过是用数组来模拟计算过程。
例如两个大整数分别为998877665544332211和112233445566778899,按照T=4,K=10000的参数设定,分别存储在整型数组a和b中,数组大小都是N,它们的加法运算(c=a+b)过程如图所示:

大整数减法
同样的,大整数的减法过程与一般的整数减法也是类似的,从低位开始,同位置的数相减,被减数小于减数时,被减数向高位借1,当T=4,K=10000时,借一位相当于加10000。特别的,倘若被减大整数小于减数大整数,则先交换它们,然后再做减法,最后为结果添加负号,为了方便起见,本关卡的测试数据保证被减数大于减数。
对于上面的大整数a=998877665544332211和大整数b=112233445566778899,它们的减法运算(c=a−b)过程如下图所示:

大整数与整数的乘法
我们知道整数之间的乘法是逐位相乘,然后相加。对于大整数与整数之间的乘法,则是把“位”扩展成了“块”,即大整数的每个数组单元分别与整数相乘,然后加上进位(初始为0),并把结果放在对应位置上,若超过了进制K,则进位,以此类推。
例如大整数123456789和整数12345,按照T=4,K=10000的参数设定,大整数存储在整型数组d中,数组大小为N,整数存储在整型变量p中,它们的乘法运算(c=d×p)过程如图所示:

大整数乘法
我们已经知道了大整数与整数之间的乘法运算,对于大整数a与大整数b的乘法运算则是大整数与整数乘法运算的拓展,也就是说,将大整数a分别与大整数b的每个数组单元相乘,然后放置在相应位置上,并累加进位。
对于上面的大整数a=998877665544332211和大整数b=112233445566778899,它们的乘法运算(c=a×b)过程如下图所示:
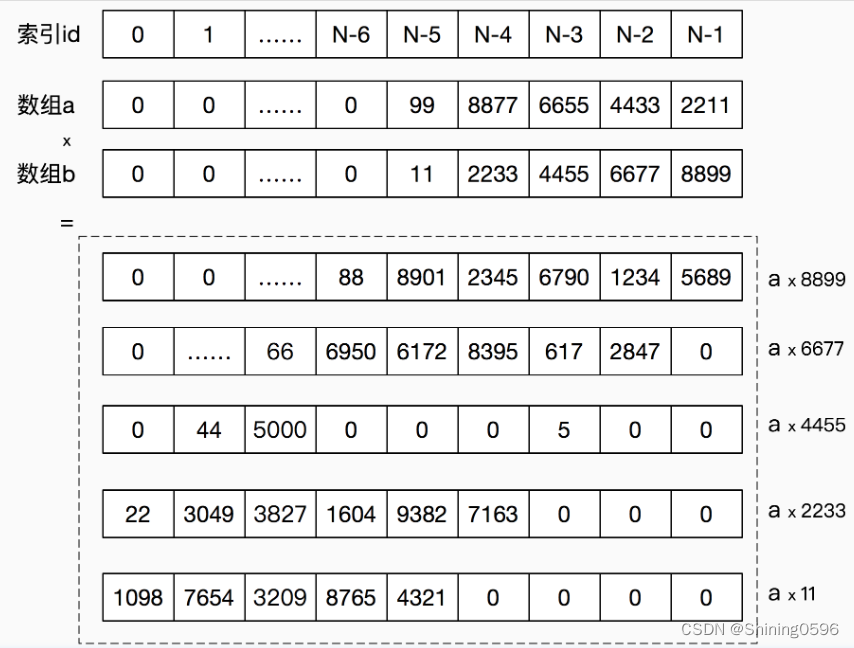

大整数与整数的除法
大整数d与整数p的除法运算保留商和余数,其中商仍然可能是大整数,而余数则是比除数要小的整数。大整数作为被除数,从高位开始,依次(从左到右i=0→N−1)将每个数组单元d[i]除以除数p,当前整除结果作为商存储在数组c对应的高位c[i]中,余数保留到下一个数组单元的计算中,依次类推,最后的余数则是大整数被除尽后的剩余项。
对于上面的大整数d=123456789和整数p=12345,它们的除法运算(c=d/p,r=d过程如下图所示:

n的阶乘求解思路
n的阶乘是一个非常大的整数,首先需要运用大整数的基本运算法则求得n!的数值。这一步可以借助大整数与整数的乘法运算,然后循环n−1次乘法即可得到n!。
n!=1×2×3×..×n
其次是统计n!中数字0的个数,因为大整数在数组中是分块存储的,所以有两种统计方式(记n!=M):
-
借助大整数与整数的除法运算:让M除以10,判断余数r是否为0,若为r=0,则答案累加1,然后将M赋值为商c,即M=c,重复以上步骤,直到M=0,程序结束;
-
借助大整数在数组中的分块存储方式:循环枚举大整数n!的数组单元,计算每个单元里的整数包含数字0的个数,最后进行累加求和即为答案。注意,每个整数单元里的数值不一定为T=4位,比如M[i]=102,当i不是大整数的头时,M[i]的真实数据为0102,包含两个数字0(一个简单的处理技巧:将M[i]加上K=10000,即M[i]+K=10102,然后判断它所包含的数字0的个数)。

编程要求
本关的编程任务是补全右侧代码片段
calc中Begin至End中间的代码,具体要求如下: -
在
calc中,根据大整数的基本运算原理,计算整数n的阶乘,并统计出n!中数字0的个数,然后将统计结果作为函数返回值。
测试说明
平台将自动编译补全后的代码,并生成若干组测试数据,接着根据程序的输出判断程序是否正确,测试数据保证10001>n>0。
以下是平台的测试样例:
测试输入: 10 预期输出: 2
输入格式: 第1行:整数n 输出格式: 第1行:n!中数字0的个数
Tips:注意整数乘法越界的情况
//
// main.cpp
// step1
//
// Created by ljpc on 2018/12/4.
// Copyright © 2018年 ljpc. All rights reserved.
//
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
// 最大长度N,分块长度K
const int N = 10001;
const int K = 10000;
const int T = (int)log10(K); // K=10000, T=4
void char_to_int(char *s, int *c)
{
// *s = 1234567890
// *c = 0000 .... 0012 3456 7890 (K=10000, T=4, c[0] c[1] .... c[N-2] c[N-1])
// i = 0 N-3 N-2 N-1 (c的下标索引i)
int L = (int)strlen(s);
for (int i=N-1; i>=0; i--) {
c[i] = 0;
if (L>=0) {
for (int j=0; j<T; j++) {
if (L-T+j < 0) {
continue;
}
c[i] = c[i] * 10 + s[L-T+j] - '0';
}
L -= T;
}
}
}
void output(int *c)
{
// *c = 0000 .... 0012 3456 7890 (K=10000, T=4, c[0] c[1] .... c[N-2] c[N-1])
// i = 0 N-3 N-2 N-1 (c的下标索引i)
// out= 1234567890
bool flag = true;
for (int i=0; i<N; i++) {
if (flag && c[i]==0) {
continue;
}
if (flag) { // 第一个非0数字:大数的头块
printf("%d", c[i]);
flag = false;
}
else { // 大数头块之后的 T 数字块
int TK = K/10;
int tmp = c[i];
while (TK) {
printf("%d", tmp/TK);
tmp %= TK;
TK /= 10;
}
}
}
printf("\n");
}
void add(int *a, int *b, int *c)
{
int carry = 0;
for (int i=N-1; i>=0; i--) {
c[i] = 0;
c[i] = a[i] + b[i] + carry;
carry = c[i] / K;
c[i] = c[i] % K;
}
}
void sub(int *a, int *b, int *c)
{
int borrow = 0;
for (int i=N-1; i>=0; i--) {
c[i] = 0;
c[i] = a[i] - b[i] - borrow;
if (c[i] >= 0) {
borrow = 0;
}
else {
c[i] = c[i] + K;
borrow = 1;
}
}
}
void mul1(int *a, int b, int *c)
{
long long tmp = 0;
int carry = 0;
for (int i=N-1; i>=0; i--) {
tmp = (long long)a[i] * (long long)b + (long long)carry;
c[i] = (int)(tmp % K);
carry = (int)(tmp / K);
}
}
void mul2(int *a, int *b, int *c)
{
long long tmp = 0;
int carry = 0;
for (int i=N-1; i>=0; i--) {
c[i] = 0;
}
for (int i=N-1; i>=0; i--) { // b[i]
carry = 0;
for (int j=N-1, idc=i; j>=0&&idc>=0; j--, idc--) { // a[j]
tmp = (long long)a[j] * (long long)b[i] + (long long)carry + (long long)c[idc];
c[idc] = (int)(tmp % K);
carry = (int)(tmp / K);
}
}
}
int div(int *a, int b, int *c)
{
long long tmp = 0;
int remain = 0;
for (int i=0; i<N; i++) {
tmp = (long long)a[i] + (long long)remain * (long long)K;
c[i] = (int)(tmp / b);
remain = (int)(tmp % b);
}
return remain;
}
int calc(int n)
{
// 请在这里补充代码,完成本关任务
/********* Begin *********/
int a[N] = {0};
int c[N] = {0};
a[N-1] = 1;
for (int i=2; i<=n; i++) {
mul1(a, i, c);
for (int j=0; j<N; j++) {
a[j] = c[j];
c[j] = 0;
}
}
int tot = 0;
/* 方法一
while (1) {
bool flag = true;
for (int i=0; i<N; i++) {
if (a[i]) {
flag = false;
break;
}
}
if (flag) {
break;
}
int r = div(a, 10, c);
if (r==0) {
tot++;
}
// a = 10 * c + r
for (int j=0; j<N; j++) {
a[j] = c[j];
c[j] = 0;
}
}
*/
// 方法二
int tmp = 0;
bool flag = true;
for (int i=0; i<N; i++) {
if (flag && a[i]==0) {
continue;
}
if (flag) {
tmp = a[i];
flag = false;
}
else {
tmp = a[i] + K;
}
while (tmp) {
if (tmp % 10 == 0) {
tot++;
}
tmp /= 10;
}
}
return tot;
/********* End *********/
}
int main(int argc, const char * argv[]) {
int n;
scanf("%d", &n);
int tot = calc(n);
printf("%d\n", tot);
return 0;
}