前言

大家好,我是最爱吃兽奶,这篇博客给大家介绍一下二分查找,我们先从最基本的开始讲解,再慢慢深入,把优化和变形也和大家说一下,那么,跟着我的步伐,我们一起去看看吧!

一、什么是二分查找?

二分查找(Binary Search)也称作折半查找

二分查找的效率很高,每查找一次,查找对象的数量就会减半

条件:要查找的元素集合必须有序

二、二分查找的实现

1.基础版

需求: 给定一个升序数组,要求我们查找数组中是否包含目标元素tmp,如果存在,则返回索引,不存在返回-1

接下来,我们就以这个数组为你进行讲解
int[] arr = {7, 13, 21, 30, 38, 44, 52, 53};

你可以打开你的编译器试着写写,思考之后再往下看效果更好哦

相信你已经写完了吧,那么我们来试着分析一下吧!

代码

    public static int BinarySearchBalance(int [] arr,int target){

        // 定义左右边界
        int left = 0;
        int right = arr.length-1;

        // 循环终止条件 left<=right
        while (left<=right) {
            int mid = (left+right)/2;

            if(target<arr[mid]){
                // 表示目标值在中间值的左边,向左缩小范围,令right = mid-1;
                right = mid-1;
            }else if(target > arr[mid]){
                // 表示目标值在中间值的右边,向右缩小范围,令right = mid+1;
                left = mid+1;
            }else{
                // target == arr[mid] 找到了,直接返回target处的下标
                return mid;
            }
        }
        // 循环结束,此时left>right,表名该数组中没有目标元素,直接返回-1
            return -1;
    }
}

经过了上面的解释,你是不是恍然大明白了呢?

不理解的话,欢迎评论区留言,有需要指点的地方也请评论区留言

那么接下来,就开启我们的进阶之旅吧!

2.进阶版

我们先来思考一下,基础版的代码是否有问题?

相比你们都清楚,是有问题的,要不然怎么会有进阶版呢?

问题1: int mid = (left+right) / 2 有什么问题?

如果right的值为 Integer.MAX_VALUE-1 ,那么第二次循环时将有可能越界

当target<arr[mid]的时候,left = mid+1 ,(left+right)的值会超过int类型所能接受的最大值,会直接变成负数,导致mid为负值,在此时如果调用arr[mid] 会报异常

解决办法: int mid = (left+right)>>>1;

>>>: 无符号右移,最高位永远补零

我们在这里直接右移一位,天王老子来了mid都不可能变成负数了

问题2: 为什么left<=right 表示区间内有未比较的元素,而不是left<right?

left == right 表示它们指向的元素也会参与比较,left<right 则表示mid指向的元素参与比较

进阶版

j的位置一定不是目标元素!!!

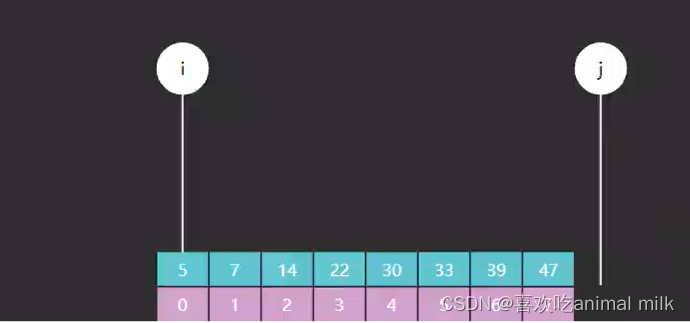
代码

    public static int BinarySearchAlternation(int[] arr,int target){
        int left = 0;
        int right = arr.length; //right 只作为边界,指向的一定不是查找目标

        while(left<right){// 表示left和right指向的元素不参与比较
            int mid = (left+right)>>>1;
            if(arr[mid]>target){
                // right 指向的元素不参与比较,不能赋值为 mid+1
                right = mid;
            } else if (arr[mid]<target) {
                left = mid+1;
            } else {
                return mid;
            }
        }
        return -1;
    }