论文十问十答:
Q1论文试图解决什么问题?
Q2这是否是一个新的问题?
Q3这篇文章要验证一个什么科学假设?
Q4有哪些相关研究?如何归类?谁是这一课题在领域内值得关注的研究员?
Q5论文中提到的解决方案之关键是什么?
Q6论文中的实验是如何设计的?
Q7用于定量评估的数据集是什么?代码有没有开源?
Q8论文中的实验及结果有没有很好地支持需要验证的科学假设?
Q9这篇论文到底有什么贡献?
Q10下一步呢?有什么工作可以继续深入?
论文相关
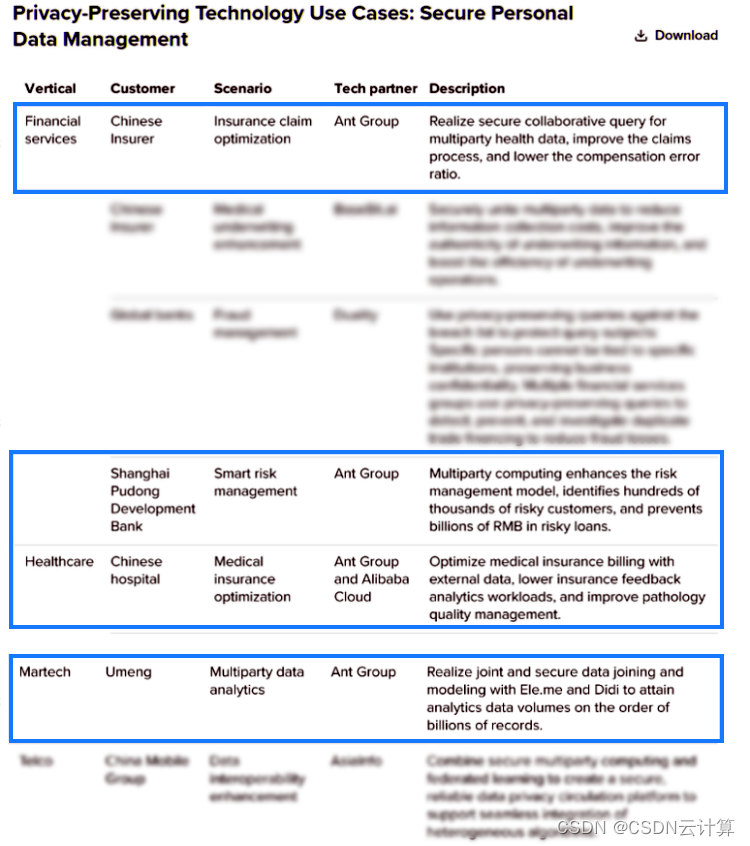
论文标题:glove:Word表示的全局向量
发表时间:2014
领域:自然语言处理-词向量经典论文
发表期刊:Association for Computational Linguistics(1区)
相关代码:http://nlp.stanford.edu/projects/glove/
数据集:
摘要
最近学习单词向量空间表示的方法已经成功地利用向量算术捕获了细粒度的语义和句法规律,但这些规律的起源仍然不清楚。我们分析并明确了在词向量中出现这些规律所需的模型性质。结果是一个新的全局对数线性回归模型,它结合了文献中两个主要模型族的优势:
- 全局矩阵分解和局部上下文窗口方法。
- 我们的模型通过只训练词-词共现矩阵中的非零元素,而不是训练整个稀疏矩阵或大型语料库中的单个上下文窗口,有效地利用了统计信息。
- 该模型产生了一个具有有意义的子结构的向量空间,这证明了它在最近的一个单词类比任务中的表现为75%。
- 它在相似性任务和命名实体识别方面也优于相关模型。
1.引言
语言的语义向量空间模型用一个实值向量表示每个词。这些向量可作为各种应用程序中的特征使用,如信息检索、文档分类、问题回答、命名实体识别和解析。
大多数词向量方法依赖于词向量对之间的距离或夹角作为评估这一组词表示的内在质量的主要方法。最近,Mikolov等人(2013c)引入了一种新的基于词类比的评价方案,该方案通过检查词向量之间的标量距离,而是它们的不同差异维度来探索词向量空间的更精细结构。例如,类比“king is to queen as man is to woman”应该通过向量方程king −queen = man − woman编码在向量空间中。这种评估方案倾向于产生意义维度的模型,从而捕获了分布式表示的多聚类思想。
学习单词向量的两个主要模型族是:
1)全局矩阵分解方法,如潜在语义分析(LSA)
2)局部上下文窗口方法,如Mikolov等人的跳跃图模型。目前,这两个模型族都存在明显的缺陷。统计信息,但它们在单词类比任务上表现相对较差,表明存在次优向量空间结构。虽然像LSA这样的方法有效地利用统计信息,但它们在单词类比任务上表现相对较差,表明存在次优向量空间结构。像skip-gram这样的方法可能在类比任务上做得更好,但它们很少利用语料库的统计数据,因为它们训练的是单独的局部上下文窗口,而不是全局共现计数。
在这项工作中,我们分析了产生线性意义方向所必需的模型性质,并认为全局对数双线性回归模型是合适的。我们提出了一个特定的加权最小二乘模型,该模型训练全局词-词共现计数,从而有效地利用统计数据。该模型产生了一个具有有意义子结构的单词向量空间,这由其在单词类比数据集上75%的准确率得到证明。我们还证明了我们的方法在几个单词相似性任务上,以及在一个常见的命名实体识别(NER)基准测试上,都优于当前的其他方法。
2.相关工作
2.1 矩阵分解方法
2.2 基于浅窗口的方法
3.GloVe模型
语料库中单词出现的统计数据是所有学习单词表示的无监督方法的主要信息来源,尽管现在有许多这样的方法,但问题仍然是是如何从这些统计数据中产生意义的,以及由此产生的单词向量可能如何表示这个意思。在本节中,我们将阐明这个问题。
3.1 构建共现矩阵
我们使用我们的见解来构建了一个新的单词表示模型,我们称之为GloVe,对于全局向量,因为全局语料库统计数据是由模型直接捕获的。
首先,我们建立了一些符号。让word-word共现计数的矩阵用X表示,其中
- X i j X_{i j} Xij表表示词j在词i的上下文中出现的次数。
- X i = ∑ k x i k X_i=\sum_{k}x_{ik} Xi=∑kxik为任何单词在单词i的上下文中出现的总次数。
-
P
i
j
=
P
(
j
∣
i
)
=
X
i
j
/
X
i
P_{i j} = P(j|i)= X_{i j}/X_i
Pij=P(j∣i)=Xij/Xi为单词j出现在单词i的上下文的概率。
我们从一个简单的例子开始,它展示了如何从共现概率中直接提取意义的某些方面。考虑两个词i和j,它们表现出一个特定的兴趣方面;为了具体起见,假设我们对热力学相的概念感兴趣,为此我们可以取i=ice和j=steam。这些词之间的关系可以通过研究它们与不同探测词的共现概率比值k来检验。因为单词k与ice有关,但与stream无关,假设k=solid,我们预计 P i k / P j k P_{ik} /P_{jk} Pik/Pjk的比率会很大。同样地,对于与stream而不是ice有关的单词k,比如k=gas,这个比率应该很小。对于像water或fasion这样的词k,要么与ice和steam有关,要么与两者都无关,这个比例应该接近于1.表1显示了这些对于大语料库的概率及其比率,这些数字证实了这些期望。
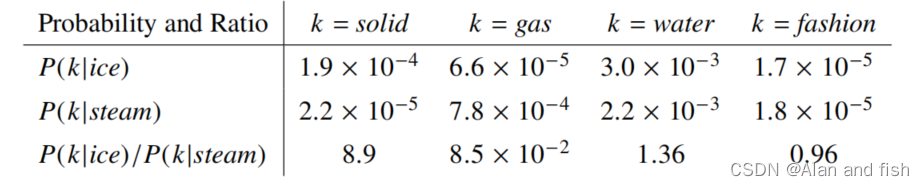
表1:从60亿个标志性语料库中选择的目标词ice和steam的共现概率。只有在这个比率中,来自water和fation等非区别性词的噪音才会被抵消,因此大值(远远大于1)与ice的相关性很好,而小值(远远小于1)与steam的相关性。
与原始概率相比,该比率能更好地区分相关单词(固体和气体)和不相关单词(水和时尚),也能更好地区分两个相关单词。
我的理解:水和冰,水和蒸汽的相关性比较大于是他们的相关性的比值就接近1,fashion与冰和蒸汽的相关性都很小,则他们的相关性比值也接近于1,冰于固体的相关性大,与蒸汽的相关性小,则他们的相关性比值就接大于1.
上述论证表明,单词向量学习的适当起点应该是共现概率的比率,而不是概率本身。注意到
P
i
k
/
P
j
k
P_{ik} /P_{jk}
Pik/Pjk的比率取决于三个单词i、j和k,最一般的模型采用的形式是,
公式
1
:
F
(
w
i
,
w
j
,
w
~
k
)
=
p
i
k
p
j
k
公式1:F(w_i,w_j,\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}}
公式1:F(wi,wj,w
k)=pjkpik
可以得到这种关系:
| ratio(i,j,k) | 单词j,k相关 | 单词j,k不相关 |
|---|---|---|
| 单词i,k相关 | 趋近1 | 很大 |
| 单词i,k不相关 | 很小 | 趋近于1 |
==========================================================
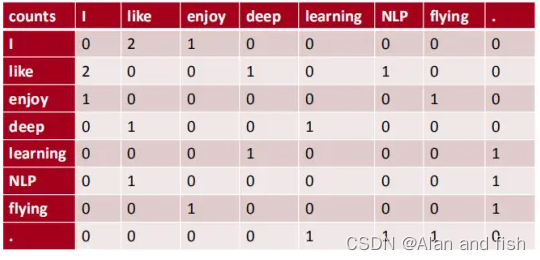
举个共现矩阵构建的例子:
F(w, wj, w)
例如:语料库如下:
- llike deep learning.
- I like NLP.
- I enjoy flying.
则共现矩阵表示如下: (使用对称的窗函数(左右window length都为1) )
===============================================================
3.2 推导代价函数
简单的公式推导过程如下:
最终代价函数:
J
=
∑
i
,
j
=
1
V
f
(
X
i
j
)
(
w
i
T
+
b
i
+
b
~
j
−
l
o
g
X
i
j
)
2
最终代价函数:J=\sum_{i,j= 1}^{V}{f(X_{ij})(w^T_i+b_i+\widetilde{b}_j-logX_{ij})^2}
最终代价函数:J=i,j=1∑Vf(Xij)(wiT+bi+b
j−logXij)2
下面是其推导过程:
| 序号 | 公式 | 原理分析 |
|---|---|---|
| 1 | F ( w i , w j , w ~ k ) = p i k p j k F(w_i,w_j,\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}} F(wi,wj,w k)=pjkpik | 这是一个假设,假设F函数是可以计算他们之间的共现关系,其中 P i k / P j k P_{ik} /P_{jk} Pik/Pjk的比率取决于三个单词i、j和k |
| 2 | F ( ( w i − w j ) T , w ~ k ) = p i k p j k F((w_i-w_j)^T,\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}} F((wi−wj)T,w k)=pjkpik | 因为单词i和单词j都在同一个向量空间中,因此他们之间的关系可以用作差来表示 |
| 3 | F ( ( w i − w j ) T w ~ k ) = p i k p j k F((w_i-w_j)^T\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}} F((wi−wj)Tw k)=pjkpik | 因为右边的比值是一个标量,所以左边的公式自然而然的想到使用内积计算得到一个标量 |
| 4 | F ( ( w i T w ~ k ) − ( w j T w ~ k ) ) = p i k p j k F((w_i^T\widetilde{w}_k)-(w_j^T\widetilde{w}_k))= \frac{p_{ik}}{p_{jk}} F((wiTw k)−(wjTw k))=pjkpik | 将括号中的公式,展开得到此公式 |
| 5 | e x p ( ( w i T w ~ k ) − ( w j T w ~ k ) ) = e x p ( w i T w ~ k ) e x p ( w j T w ~ k ) = p i k p j k exp((w_i^T\widetilde{w}_k)-(w_j^T\widetilde{w}_k))=\frac{exp(w_i^T\widetilde{w}_k)}{exp(w_j^T\widetilde{w}_k)}= \frac{p_{ik}}{p_{jk}} exp((wiTw k)−(wjTw k))=exp(wjTw k)exp(wiTw k)=pjkpik | 令F为指数函数,则取指数函数,拆分得到一个分式 |
| 6 | e x p ( w i T w ~ k ) = p i k = X i k X i exp(w^T_i\widetilde{w}_k)=p_{ik}=\frac{X_{ik}}{X_i} exp(wiTw k)=pik=XiXik | 公式等价代换得到关于i和j的公式 |
| 7 | w i T w ~ k = l o g ( p i k ) = l o g ( x i k ) − l o g ( X k ) w^T_i\widetilde{w}_k=log(p_{ik})=log(x_{ik})-log(X_k) wiTw k=log(pik)=log(xik)−log(Xk) | 两边取对数函数 |
| 8 | l o g ( X i k ) = w i T w k + l o g ( x i ) log(X{ik})=w^T_iw_k+log(x_i) log(Xik)=wiTwk+log(xi) | 两边进行移项 |
| 9 | l o g ( X i k ) = w i T w k + b i + b k log(X{ik})=w^T_iw_k+b_i+b_k log(Xik)=wiTwk+bi+bk | 因为 l o g ( x i ) log(x_i) log(xi)与k无关,所以将其吸收为偏置项 |
| 10 | J = ∑ i , j = 1 V ( w i T + b i + b ~ j − l o g X i j ) 2 J=\sum_{i,j= 1}^{V}{(w^T_i+b_i+\widetilde{b}_j-logX_{ij})^2} J=∑i,j=1V(wiT+bi+b j−logXij)2 | 因为上面的值只是理想状态,因此我们要通过计算机计算得到相关的参数值,拟合他,J则为其代价函数 |
但是上述的代价函数还需要使用一个权重函数f(x),解决一些特殊的情况,需要考虑到下面这些因素:
- 当 x i k = 0 x_{ik}=0 xik=0的时候,则J的值必须为0,比如两个词语之间重来没有一起出现过,则值应该为0
- f(x)必须是一个非减函数,这样罕见的非共现关系就不会被夸大
- 对于x的大值,f (x)应该相对较小,这样频繁的共出现就不会被夸大。
最终得到权重函数为:
f ( x ) = { ( x / x m a x ) α 当 x < x m a x 时 1 其他情况 f(x)=\begin{cases} (x/x_{max})^α & 当x<x_{max}时 \\ 1 & 其他情况 \end{cases} f(x)={(x/xmax)α1当x<xmax时其他情况
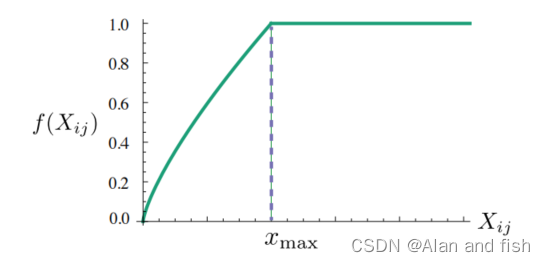
图1:权重函数图像,其中α=3/4
=========================================================================
下面为详细的推导过程:
其中w∈
R
d
R^d
Rd是词向量,词向量和
w
~
\widetilde{w}
w
∈
R
d
R^d
Rd是单独的上下文词向量,其作用将在第4.2节中讨论。在这个方程中,右侧从语料库中提取,F可能依赖于一些尚未指定的参数。F的可能性是巨大的,但通过强制执行一些需求,我们可以选择一个独特的选择。首先,我们希望F对单词向量空间中
P
i
k
/
P
j
k
P_{ik} /P_{jk}
Pik/Pjk的比率的信息进行编码。由于向量空间本质上是线性结构,所以最自然的方法是利用向量差。为了达到这个目的,我们可以只考虑那些只依赖于两个目标词的差值的函数F,即修改公式(1)为:
公式
2
:
F
((
w
i
−
w
j
)
T
,
w
~
k
)
=
p
i
k
p
j
k
公式2:F((w_i-w_j)^T,\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}}
公式2:F((wi−wj)T,w
k)=pjkpik
接下来,我们注意到公式2中F的参数。左边是向量,而右边是一个标量。虽然F可以被认为是一个复杂的函数,参数化,例如,一个神经网络,这样做会混淆我们试图捕获的线性结构。为了避免这个问题,我们可以首先取参数的点积,得到公式(3):
公式
3
:
F
((
w
i
−
w
j
)
T
w
~
k
)
=
p
i
k
p
j
k
公式3:F((w_i-w_j)^T\widetilde{w}_k)= \frac{p_{ik}}{p_{jk}}
公式3:F((wi−wj)Tw
k)=pjkpik
从而防止F以不希望的方式混合矢量维度。接下来,请注意,对于单词共现矩阵,单词和上下文词之间的区别是任意的,我们可以自由地交换这两个角色。为了始终做到这一点,我们不仅必须交换w↔
w
~
\widetilde{w}
w
,而且还要交换X↔
X
T
X^T
XT。我们最终的模型在这个重新标记下应该是不变的,但是公式(3)并不是。然而,对称性可以分两步恢复。首先,我们要求F是群(R,+)和(R>0,×)之间的同态,即:
公式
4
:
F
(
(
w
i
−
w
j
)
T
w
~
k
)
=
F
w
i
T
w
~
k
F
w
j
T
w
~
k
公式4:F((w_i-w_j)^T\widetilde{w}_k)= \frac{F_{w^T_i\widetilde{w}_k}}{F_{w^T_j\widetilde{w}_k}}
公式4:F((wi−wj)Tw
k)=FwjTw
kFwiTw
k
其中,由公式(3)和公式(4)等价代换得到公式(5):
公式
5
:
F
(
w
i
T
w
~
k
)
=
p
i
k
=
X
i
k
X
i
公式5:F(w^T_i\widetilde{w}_k)=p_{ik}=\frac{X_{ik}}{X_i}
公式5:F(wiTw
k)=pik=XiXik
令F为指数函数exp,则两边取对数得到公式(6):
公式
6
:
W
i
T
w
~
k
=
l
o
g
(
P
i
k
)
=
l
o
g
(
X
i
k
)
−
l
o
g
(
X
i
)
公式6:W^T_i\widetilde{w}_k=log(P_{ik})=log(X_{ik})-log(X_i)
公式6:WiTw
k=log(Pik)=log(Xik)−log(Xi)
接下来,我们注意到公式(6)如果没有右边的log(
X
i
X_i
Xi),将显示交换对称。然而,这个项与k无关,所以它可以被吸收成wi的偏置。最终,为
w
~
k
\widetilde{w}_k
w
k增加一个额外的偏置
b
~
k
\widetilde{b}_k
b
k可以恢复对称性,
公式
7
:
w
i
T
w
~
k
+
b
i
+
b
~
k
=
l
o
g
(
X
i
k
)
公式7:w^T_i\widetilde{w}_k+b_i+\widetilde{b}_k=log(X_{ik})
公式7:wiTw
k+bi+b
k=log(Xik)
公式(7)是对公式(1)的一种巨大的简化。但它实际上是不定义的,因为只要它的参数为零时,对数就会发散。解决这个问题的一个方法是在
l
o
g
(
X
i
k
)
→
l
o
g
(
1
+
X
i
k
)
log(X_{ik})→log(1 + X_{ik})
log(Xik)→log(1+Xik)中包含一个加法的移位,它保持X的稀疏性,同时避免发散。将共现矩阵的对数进行因子分解的想法与LSA密切相关,我们将在实验中使用所得到的模型作为基线。这个模型的一个主要缺点是,它平均权衡所有并发事件,即使是那些很少或从未发生的事件。这种罕见的同时出现比频繁的出现携带的信息更少——但即使是零条目占X数据的75-95%,这取决于词汇表大小和语料库。
我们提出了一个新的加权最小二乘回归模型来解决这些问题。得到等式(7)作为一个最小二乘问题,并在代价函数中引入一个加权函数
f
(
X
i
j
)
f(X_{i j})
f(Xij),得到了这个模型.
公式
8
:
J
=
∑
i
,
j
=
1
V
f
(
X
i
j
)
(
w
i
T
+
b
i
+
b
~
j
−
l
o
g
X
i
j
)
2
公式8:J=\sum_{i,j= 1}^{V}{f(X_{ij})(w^T_i+b_i+\widetilde{b}_j-logX_{ij})^2}
公式8:J=i,j=1∑Vf(Xij)(wiT+bi+b
j−logXij)2
其中,V是词汇表的大小。加权函数应遵循以下特性:
- f (0) = 0.如果f被视为一个连续函数,它应该以x→0的速度消失,使得 l i m x → 0 f ( x ) l o g x 2 lim_{x→0}f(x)log^2_x limx→0f(x)logx2是有限的.
- f (x)应该是非递减的,这样罕见的非共现关系就不会被夸大。
- 对于x的大值,f (x)应该相对较小,这样频繁的共出现就不会被夸大。
当然,有大量的函数满足这些性质,但我们发现有一类工作得很好的函数可以参数化为:
f
(
x
)
=
{
(
x
/
x
m
a
x
)
α
当
x
<
x
m
a
x
时
1
其他情况
f(x)=\begin{cases} (x/x_{max})^α & 当x<x_{max}时 \\ 1 & 其他情况 \end{cases}
f(x)={(x/xmax)α1当x<xmax时其他情况
该模型的性能微弱地依赖于截止点,我们在所有的实验中都将其固定为
x
m
a
x
x_{max}
xmax = 100。我们发现α = 3/4比α = 1的线性版本有了适度的改进。虽然我们只提供了选择值3/4的经验动机,但有趣的是,一个类似的分数功率尺度被发现具有最佳的性能。
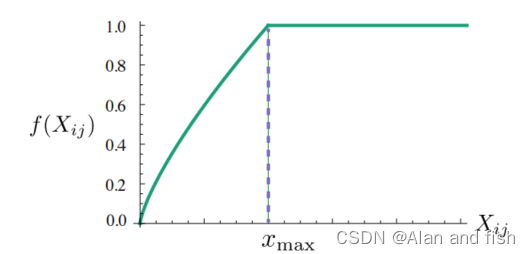
图1:权重函数图像,其中α=3/4
3.3 与其他模型的相关性
因为所有学习词向量的无监督方法最终都是基于一个语料库的发生统计量,这些模型之间应该有一些共性。然而,某些模型在这方面仍然有些不透明,特别是最近的基于windows的方法,如skip-gram和ivLBL。因此,在本小节中,我们将展示这些模型如何与我们提出的模型相关,如公式(8)中定义的。
skip-gram或ivLBL方法的起点是单词j出现在单词i的上下文的概率的模型
Q
i
j
Q_{i j}
Qij。具体来说,我们可以认为
Q
i
j
Q_{ij}
Qij是一个softmax函数,
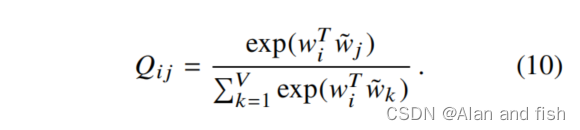
这些模型的大部分细节都与我们的目的无关,除了他们试图在上下文窗口扫描语料库时最大化日志概率之外。训练以在线随机方式进行,但隐含的全局目标函数可以写成:
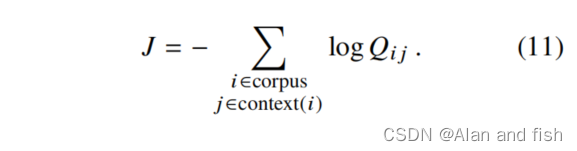
计算softmax函数中求和的每一项的归一化因子的代码比较高。为了实现有效的训练, skip-gram和ivLBL模型引入了对
Q
i
j
Q_{i j}
Qij的近似。
然而,在求和公式(11)中,如果我们首先把i和j值相同的项组合在一起,可以更有效地计算。
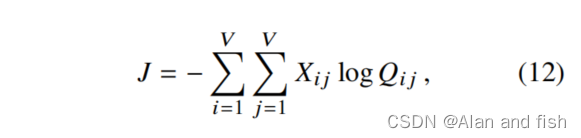
其中,我们使用了相似项的数量是由共现矩阵X给出的事实。
回顾我们
X
i
=
∑
k
X
i
k
X_i=∑_k X_{ik}
Xi=∑kXik和
X
i
=
P
i
j
=
X
i
j
/
X
i
X_i = P_{i j} = X_{i j}/X_i
Xi=Pij=Xij/Xi的计算公式,我们可以将J重写为:
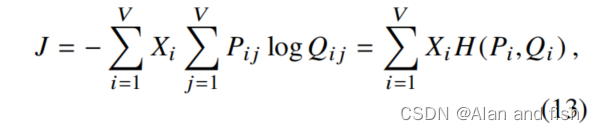
其中
H
(
P
i
,
Q
i
)
H(P_i,Q_i)
H(Pi,Qi)是
P
i
P_i
Pi和
Q
i
Q_i
Qi分布的交叉熵,其中我们将其定义为
X
i
X_i
Xi。作为交叉熵误差的加权和,该目标与方程式(8)的加权最小二乘目标具有一些形式上的相似性。 事实上,优化公式(13)是可能直接相对于在skip-gram和ivLBL模型中使用的在线训练方法。可以将这个目标解释为一个“global skip-gram”模型,进一步研究可能会很有趣。另一方面公式(13)展示了一些不可取的属性,在采用它作为学习单词向量的模型之前应该解决。
首先,交叉熵误差只是概率分布之间许多可能的距离度量之一,它有一个不幸的特性,即长尾分布往往建模得很差,给不太可能的事件太多的权重。此外,为了使度量有界,它要求模型分布Q被适当地归一化。这由于公式(10)中整个词汇表的和,提出了一个计算瓶颈,我们需要考虑一个不同的距离测量方法,它不需要Q的这个特性。一个自然的选择将是一个最小二乘目标,其中Q和P中的归一化因子丢弃。
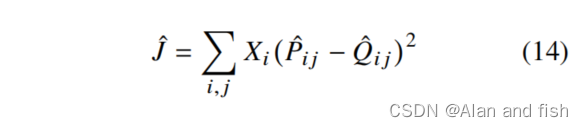
其中
P
^
i
j
=
X
i
j
\hat{P}_{ij}=X_{ij}
P^ij=Xij和
Q
^
i
j
=
e
x
p
(
w
i
T
w
~
j
)
\hat{Q}_{ij}=exp(w_i^T\widetilde{w}_j)
Q^ij=exp(wiTw
j)是非归一化分布。在这个阶段出现了另一个问题,即
X
i
j
X_{i j}
Xij经常取非常大的值,这可能会使优化复杂化。一种有效的补救方法是最小化
p
^
\hat{p}
p^和
Q
^
\hat{Q}
Q^的对数的平方误差.
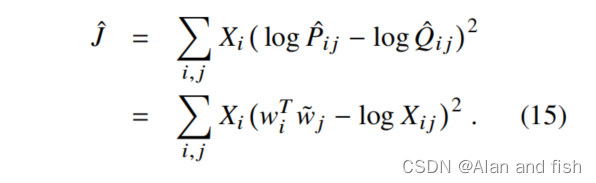
最后,我们观察到,虽然加权因子
X
i
X_i
Xi是由 skip-gram和ivLBL模型所固有的在线训练方法预先确定的,但它并不能保证是最优的。事实上,Mikolov等人(2013a)观察到,通过过滤数据可以提高性能,从而降低频繁单词的加权因子的有效值。考虑到这一点,我们引入了一个更一般的加权函数,我们也可以自由地将它依赖于上下文词。结果如下:
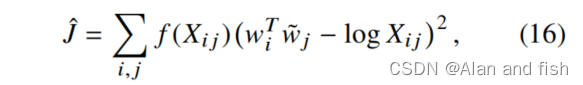
它等价于方程(8)的成本函数,这是我们之前推导出来的。
3.4 模型复杂度
从公式(8)中可以看出。加权函数f (X)的显式形式,模型的计算复杂度取决于矩阵X中非零元素的数量。由于这个数字总是小于矩阵的入口总数,因此模型的规模并不比
O
(
∣
V
∣
2
)
O(|V |^2)
O(∣V∣2)差.乍一看,这似乎是对基于浅窗口的方法的一个实质性改进,该方法与语料库的规模|C|有关。然而,典型的词汇表有成千上万个单词,所以
∣
V
∣
2
|V | ^2
∣V∣2可以有数千亿个单词,这实际上比大多数语料库要大得多。由于这个原因,确定是否可以在X的非零元素的数量上放置一个更紧的界是很重要的。
为了对X中的非零元素的数量做出任何具体的陈述,有必要对词的共现现象的分布做出一些假设。特别地,我们将假设单词i与单词
X
i
j
X_{ij}
Xij的共出现次数可以被建模为该单词对的频率秩的幂律函数:
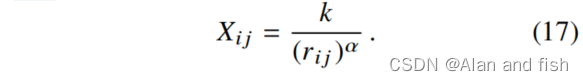
语料库中的单词总数与共出现矩阵X的所有元素的和成正比,
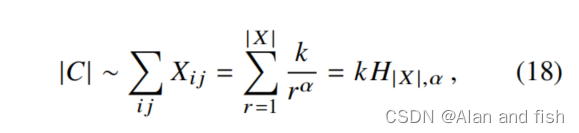
和的上限|X|是最大频率秩,它与矩阵X. T中非零元素的个数一致.这个数字也等于公式的(17)中r的最大值。这样,
X
i
j
≥
1
X_{i j}≥1
Xij≥1,即
∣
X
∣
=
k
1
/
α
|X| = k^{1/α}
∣X∣=k1/α。因此,我们可以写出公式(18)。
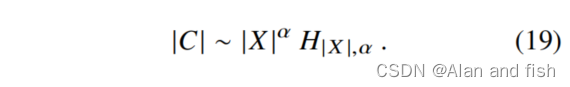
我们感兴趣的是,当两个数字都很大时,|X|与|C|之间的关系;因此,我们可以自由地展开大|X|方程的右边。为此,我们使用广义谐波数的展开式(Apostol,1976)。
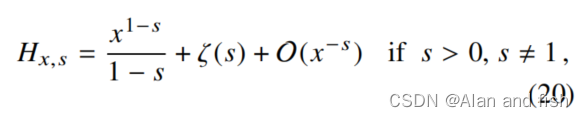
交给
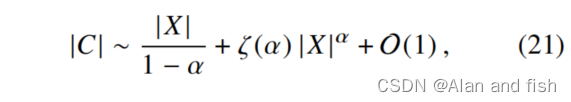
其中,ζ (s)是黎曼zeta函数。在X很大的极限下,只有公式(21)右边的两个项中的一个将会是相关的。并且它的term取决于α是否大于1.
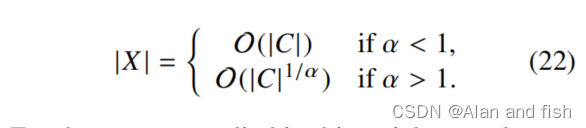
对于本文所研究的语料库,我们观察到
X
i
j
X_{i j}
Xij被公式17很好地建模。使用α = 1.25。在这种情况下,我们有
∣
X
∣
=
O
(
∣
C
∣
0.8
)
|X| = O(|C|^{0.8})
∣X∣=O(∣C∣0.8)。因此,我们得出结论,该模型的复杂性比最坏情况
O
(
V
2
)
O(V^2)
O(V2)好得多,事实上,它比类似
O
(
∣
C
∣
)
O(|C|)
O(∣C∣)的基于在线窗口的方法更好。