基于Q-learning方法的地铁列车时刻表重新调度

文章信息

《Metro Train Timetable Rescheduling Based on Q-learning Approach》是发表在2020 IEEE 23rd International Conference on Intelligent Transportation Systems (ITSC)上的一篇文章。

摘要

在地铁系统中，不可预测的干扰会影响正常运行，给乘客带来诸多不便。本文研究了地铁管理中考虑实际操作的列车时刻表改期问题。首先，建立了以改期时刻表偏差、乘客总延误时间和能耗为目标的优化模型。同时，介绍了约束条件和一些实用的重调度规则(如预编程速度曲线、列车扣留策略)。其次，将该模型重新构建为马尔可夫决策过程(MDP)，明确了状态、动作和奖励函数，然后采用提出的Q-learning方法求解。最后，以北京亦庄地铁线的运行数据为例，验证了该方法的有效性。结果表明，在短时间内可以得到优化目标之间的权衡解。

介绍

随着中国轨道交通的快速发展，地铁系统提供的快速、便捷的服务使乘客受益匪浅。但在一些不可避免的干扰场景下(如基础设施故障、设备故障)，巨大的客流需求也给运营管理带来了很大的压力。如果发车间隔较短，主要延误很容易在列车之间产生连锁反应，导致无法实施计划的列车时刻表。更重要的是，列车延误的发生会影响服务质量和乘客满意度。在这种情况下，需要及时调整计划的时刻表，以减少对乘客的负面影响。调度员的操作非常复杂，包括呼叫司机、通知站内工作人员、记录操作过程等，可能会降低重调度策略的效率。因此，有必要设计一种算法来辅助调度员处理列车延误，使列车从干扰中迅速恢复正常运行。

当由干扰引起的主要列车延误时，如果其后的列车不在其后的车站滞留，可能会导致其后的列车在该区段内停止或缓慢运行。从乘客的角度来说，如果持续一段时间，会带来很大的不适。因此，调度员会尽量安排列车在车站停靠，以避免不必要的恐慌。此外，列车运行和停站时间的调整是列车自动运行(ATO)系统中另一种最常用的基于预编程速度曲线的运行调整策略，与列车运行时间一一对应。考虑到这些实际的调度策略，本文首先在多目标TTR模型中引入了扣留策略和运行水平。从决策的角度，将模型转化为MDP模型，并提出了相应的强化学习方法。

问题描述

我们考虑的地铁线路结构如图1所示，包括上行、下行和一个折返站。车站和区段用1,2,…,2I表示。

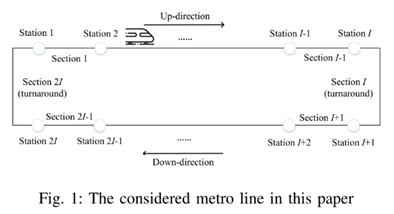
根据地铁系统的特点和实际运行情况，提出了一些假设。

1) 由于地铁系统布局单一，车站通常没有侧线。从这个意义上说，本文不允许超车和交叉策略。换句话说，所有的列车都以先进先出的方式运行，并在每个车站停车。

2) 某一运营级别对应的特定路段的运行时间是一个固定值，因为ATO系统预先编程了速度曲线。

3) 不考虑外部因素，如极端天气、地震等导致完全中断运行的情况。

A. 目标函数

本文从计划时刻表与改期时刻表的偏差、能耗和乘客总延误时间三个方面考虑优化目标。

TTR问题首先是为了尽快恢复正常的运行秩序和计划的时间表。Tdeviation用于表示计划时间表与改期时间表的偏差之和，具体表示如下

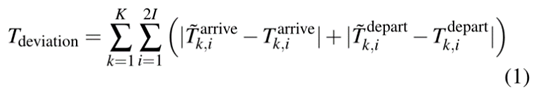
其中T~arrive k,i和Tarrive k,i分别代表列车k到达i站的计划时间和重新安排的时间；T~depart k,i和Tdepart k,i分别代表k次列车从i站出发的计划时间和改期时间；K是需要改期列车数量的总和，2I是车站和路段的数量总和。

其次，列车在固定路段的能耗取决于行驶时间，而行驶时间是由运营水平决定的。一旦给出了运营水平，就可以确定这部分消耗的能量。那么总能量消耗可以由Econsume给定

式中Ek,i为列车k在第i段的能耗。

扰动下的列车延误会降低服务质量，从而影响乘客的满意度。车上乘客到达目的地的延误时间Tdelay计算为

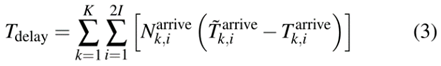
其中Narrive k,i是k次列车在i站下车的乘客人数。

综上所述，我们制定了目标函数，使这些指标的加权和最小，以达到运营成本和服务质量之间的权衡，即

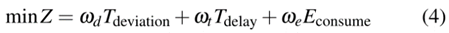
式中ωd、ωt、ωe为权重系数，表示不同指标的重要性。

B. 约束

1) 车头时距约束：为了保证安全，列车必须满足一定的车头时距，这是通过下限来保证的。只要同一站点相邻列车的到站和发站时间被限制，这些约束条件就会得到满足，写为

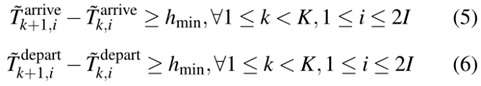
其中hmin为最小车头时距。

2) 运行和停站时间约束：如上所述，这里考虑ATO系统中预编程的速度曲线。因此，运行时间由运营水平唯一决定。设δl k,i和ηn k,i为表示是否选择运营水平l或n的二元变量，对运行和停站时间的约束公式为

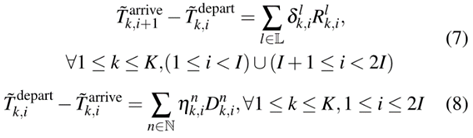
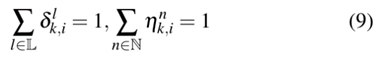
其中Rl k,i为运营水平l的运行时间，Dn k,i为运营水平n的停站时间。由式(9)可知，k次列车在i段或i站只能选择一种运营水平。

3) 折返约束：列车到达I站后，会折返并改变行驶方向。因此，我们使用周转约束来指定列车返回所需的时间，它被描述为

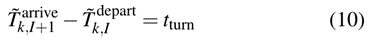
其中tturn是I站的折返时间。

4) 列车运力约束：本文建立客流需求OD矩阵，预测动态客流，计算列车延误的负面影响，定义为

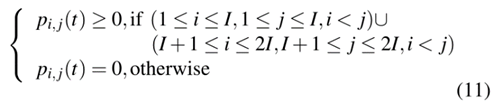
列车延误将不可避免地导致站台拥挤。在这种情况下，由于运力限制，站台上的乘客可能无法同时全部上车。根据OD矩阵，可以得到在i站可以登上k次列车的候车乘客数量。它不仅与i站的乘客到站率有关，还取决于是否有乘客无法登上上一趟列车。Tw k,i定义为最后一名在i站登上k次列车的乘客进入该站的时间，则列车运力约束可表示为

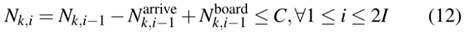
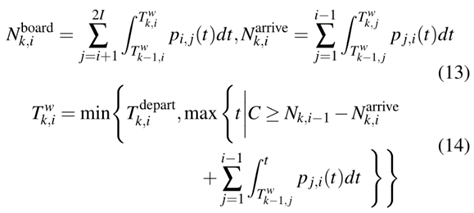
式中，C为列车运力；N k,i为k次列车到达i站时车上的乘客人数；N arrive k,i是在i站登上k次列车的乘客人数。特别地，N k,0=N arrive k,0=N depart k,0=0。

5) 动力学约束：为了便于能量计算，有必要建立一些动力学约束。列车在区段运行一般分为加速、巡航、滑行和制动四个阶段，分别用tl,a k,i、tl,c k,i、tl,o k,i和tl,b k,i表示。一般认为只有前两个阶段有能量消耗。阻力按产生方法分为基本阻力和附加阻力两种。在实际应用中，基本阻力基本遵循戴维斯公式。对于附加阻力，考虑了梯度因子。所以t时刻的牵引力可以由下式获得

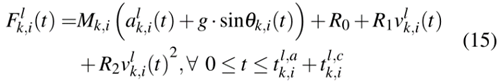
式中，Mk,i为列车质量，等于列车净重与车上乘客质量之和；R0、R1、R2为Davis公式的系数；al k,i(t)， vl k,i(t)分别为列车k在t时刻速度水平为l时的加速度和速度;θk,i(t)为列车k在运行时间t时第i段的路径梯度。

根据机械功率方程，能量消耗可由牵引力乘以速度的积分计算，即为

C. 列车扣留策略

目前调度员处理延误的方法有：(1)缩短路段运行时间；(二)扣留跟随列车；(3)利用备用列车；(4)让列车在中间站折返。本文基于方法(1)和方法(2)重点研究TTR问题。通过上述分析，可以通过调整运营水平来缩短运行时间。其次介绍了列车扣留策略。

在实际的地铁系统中，跟随列车无法根据主要延误实时调整车速。因此，如果由扰动引起的主要延误违反了安全约束，接下来的列车需要被调度员在随后的车站扣留。图2描述了一个应用列车扣留策略的例子，其中计划时刻表为黑色实线，重新安排的时刻表为橙色虚线。当列车1因车辆故障无法从4号站开出时，2、3、4次列车需分别扣留在3、2、1号站，直至满足最小车头时距。

至于如何确定列车是否需要扣留，我们关注的是上一趟列车的发车时间。定义二元变量µk,i为使用列车扣留策略的标志，表示为

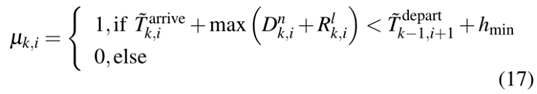
经判定需扣留的列车，应相应调整停运时间。在日常运行中，即使在干扰下，列车之间的跟踪间隔也应保持。因此，可以按如下方式更改停站时间

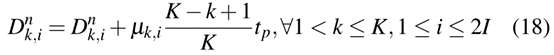
另外，如果1号站有列车扣留，则无法再实施列车扣留策略，后续列车到达该站的时间调整如下

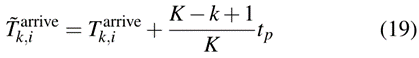
基于Q-learning方法的列车时刻表调整

Q-learning方法是强化学习(RL)的内容，适用于处理多阶段决策。为了解决上述问题，我们在本节中首先将模型转换为马尔可夫决策过程(MDP)，以便于理解。在此基础上，提出了一种基于查找表的调整时刻表获取算法。

A. MDP的基本要素

MDP是描述从交互中学习的问题的框架。在智能体和环境的交互作用下，通过试错来改变决策。具体地说，在智能体选择动作之后，环境更新并返回奖励。在本文中，智能体的任务就是使这些奖励最大化。接下来，详细介绍MDP中各元素的定义，如表I所示。

1) 状态和动作：为了解决奖励和转移函数的计算，每个状态都应该有相应的记录信息，称为状态变量。列车k在i站的状态变量定义为

其中状态变量N onboard i (k)为车上乘客人数；T arrive i (k)表示k次列车到达i站的时间。

这些动作对应于优化模型的决策变量，即列车的停站时间和运行时间。因此，每个状态的动作定义为

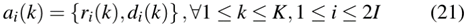
其中ri(k)表示第i次列车在k站的停站时间，di(k)表示第i次列车在k站之前的运行时间。具体来说，rI(k)和r2I(k)是周转时间。

2) 奖励函数：列车时刻表调整问题以能量消耗、时刻表偏差和乘客的延误时间为目标，由式(4)表示，则状态Si(k)和动作ai(k)的奖励为

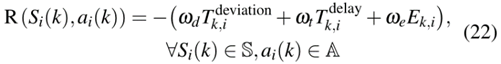
其中S是所有可能状态的集合，A是所有可以选择的可行动作的集合。

3) 状态转移函数：状态转移函数SM涉及上车人数和列车节点的变化。乘客转移规律由式(12)描述。列车节点不仅指车站指标的变化，还指列车k到达i站的时间，记为

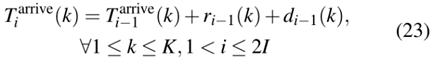
B. 求解方法

基于Q-learning方法，设计了一种有效的算法来解决本文提出的列车时刻表调整问题。Q-learning是一种近似动态规划方法，它利用近似结构逼近动态规划方程中的价值函数，从而满足Bellman最优性原则。在这里，我们引入了一种使用迭代查找表和离线策略的近似方法，即学习到的价值函数与所遵循的策略无关。

建立一个矩阵来表示查找表，它的列是不同的状态，行是所有可能的动作的排列之一。然后使用ε-贪婪策略来选择动作。一旦智能体选择了一个动作，相应的查找表位置将更新如下