Shape-Aware Weakly/Semi-Supervised Optic Disc and Cup Segmentation with Regional/Marginal Consistency

摘要

1. 提出了一个弱/半监督框架，该框架具有逐像素分割概率图（PM）、几何感知的修改有符号距离函数表示（mSDF）和感兴趣局部边界区域特征（B-ROI）之间的几何关联和特定领域知识的优势。
2. 提出了一种基于双重一致性正则化的半监督范式，其中区域和边缘一致性从大量未标记数据的对象的固有区域和边界一致性中受益于所提出的模型。
3. 首次利用边界和区域之间的领域特定知识，即OD&OC的椭圆形状的周长和面积，其中提出了一个可微vCDR估计模块用于端到端训练。
4. 模型不需要任何离线后处理来生成vCDR。此外，在不需要任何额外费力的注释的情况下，对vCDR的监督可以作为OD&OC区域和边界分割的弱监督。
   代码链接

本文方法

由PM分割和mSDF回归两个任务组成。在所提出的弱/半监督学习方式中，分别利用了两个任务在区域和边界方面的几何关联。

Modified Signed Distance Function (mSDF )

先前的工作采用SDF来表示分割任务中的目标掩码，因为它使网络能够学习关于对象边界的距离感知表示，强调输入图像的空间感知。提出了一种修改的有符号距离函数（mSDF），其定义为

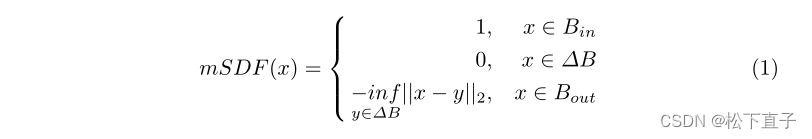
其中||x−y||2是像素x和y之间的欧几里得距离。此外，Bout、Bin和ΔB分别表示对象的外部、内部和边界。与经典SDF不同的是，在每个对象外部，mSDF取负值，与到边界的距离成比例，而在对象内部仅为1，在边界上为0。这样，双重任务可以获得连贯的语义特征，同时mSDF回归任务受益于距离感知的空间信息监督。

Dual Consistency Regularisation of Semi-Supervision

在半监督条件下，双重一致性规范化在任务层面上施加了区域和边际一致性。至于区域一致性，提出了一个转换层，以可微分的方式将mSDF转换为PM。准确地说，区域变换层ξr定义为

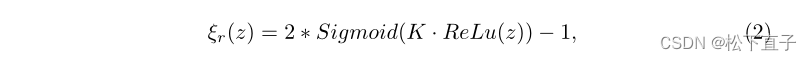
其中z表示像素x处的mSDF值；K是一个非常大的值；Sigmoid和ReLu是非线性激活函数。注意，使用S形激活函数是因为我们将OC&OD分割视为两个输出通道中的两个二进制分割。K值越大表示近似值越接近，在本工作中采用5000。利用等式2，我们可以获得变换后的分割图P M t，例如，P M t=ξr（mSDF）。对于所有未标记的输入，我们在P M和P M t之间应用Dice损失（LRu）来实施无监督的区域一致性正则化。
关于边界一致性，我们导出了PM和mSDF的空间梯度，分别作为估计的等高线。先前的研究已经证明，由于前景和背景极不平衡，这种宽度为一个像素的窄轮廓很难优化，导致一致性正则化减弱。我们不是只关注薄轮廓位置，而是考虑在相应估计轮廓的一定距离（边界宽度）内的ROI。

值得注意的是，ψ的输出宽度可以通过改变Maxpooling2D操作的内核大小、步长和填充值来确定。在这项工作中，我们根据经验将ψPM和ψmSDF的输出边界宽度设置为4个像素。在ψPM和ψmSDF之后，我们将PM和mSDF的B-ROI分别称为Bpm和BmSDF。理想情况下，BP M和BmSDF应该彼此足够接近。因此，应用BPM和BmSDD之间的Dice损失（LBu）来强制执行未标记数据的无监督边际一致性正则化。
同时，我们在BP M和BmSDF上应用骰子损失（LB）来监督标记数据的双边界预测

Differentiable vCDR estimation of Weakly Supervision

由于OD和OC的形状是椭圆形的，以前的方法采用椭圆拟合离线后处理分割预测，以提高分割精度，或者使用长轴上OD和OC近似的直径计算vCDR。然而，他们忽视了它在OD&OC细分任务中的潜在监督价值。为了解决这个问题，我们利用边界和区域之间关于椭圆形状的周长和面积的特定领域知识，以可微分的方式近似vCDR。准确地说，vCDR被定义为长轴上测量的杯状物直径除以圆盘直径的比率。同时，考虑到周边的大小以及OD和OC的面积，也可以估计这种比率。根据欧拉方法，椭圆形的面积（Ao）和周长（Po）定义为

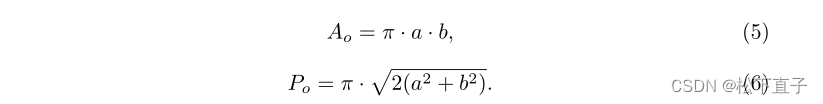
其中a和b分别表示椭圆形长轴和短轴的半轴。我们用PM的相加像素值来近似Ao，可以被视为像素级的椭圆形区域。此外，我们通过B-ROI检测层导出了PM的空间梯度（ψPM），以检测宽度为1的边界（bpm）。然后bpm的相加像素值被近似地视为Po。使用等式5和等式6，我们可以用Ao和Po来近似a

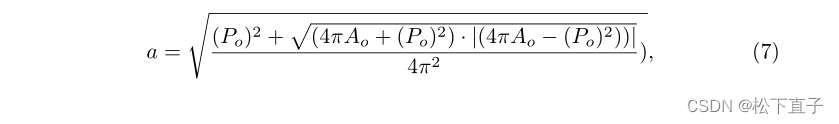
其中|·|用于防止sqrt在初始学习期间返回负值。给定方程7，我们可以用相应的Po和Ao计算OD长半轴（aOD）和OC长半轴（aOC）。然后，vCDR估计层θ可以定义为：

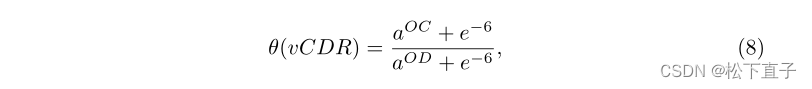
给定vCDR的预测，我们在预测和GT之间应用MSE损失（LvCDR）来完全监督vCDR估计，而弱监督OD&OC分割

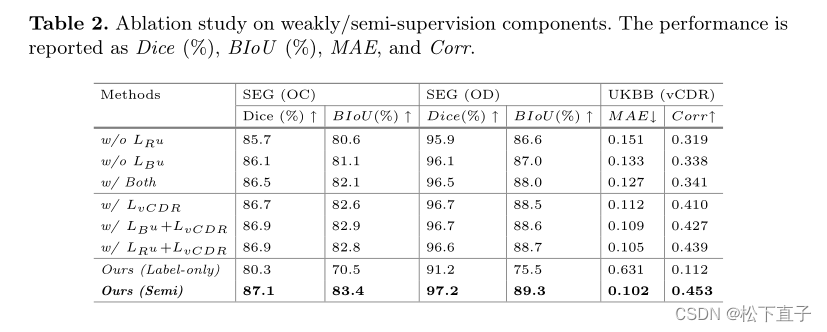
实验结果