机器学习——弹性网估计

文章目录

• 机器学习——弹性网估计
• • @[toc]
  • 1 模型介绍
  • 2 模型设定
  • 3 弹性网估计

1 模型介绍

弹性网估计属于惩罚回归，常见的惩罚回归包括岭回归(ridge)、套索回归(lasso)和弹性网(elasticnet)回归等。

岭回归用于缓解高维数据可能的多重共线性问题：当样本容量$n$小于特征变量数$p$时，采用普通最小二乘法会出现多重共线问题，无法识别特征变量对标签的影响。如果$n$不是远大于$p$，即使能识别各特征变量的影响系数，但外推能力较差。岭回归在损失函数基础上加上待估参数的L2范数，通过最小化使各变量系数向原点收缩。给定收缩参数，能识别出某些特征变量对标签的影响可能并不稳健。

套索回归在损失函数基础上加上待估参数的L1范数，这使得损失函数变得不可微，但某些变量的影响系数可能刚好等于0，使得损失函数最小化。这使套索回归具备筛选变量的功能。

弹性网估计是岭回归和套索回归的混合，尽管lasso可以筛选变量，但对于具有高度相关的多个变量，lasso会任意进行筛选，导致经济解释不足。由于ridge基本不会出现‘稀疏解’，将ridge与lasso结合，即L1范数和L2范数均融入损失函数中形成弹性网估计。

---

2 模型设定

给定多元线性回归模型
$$\mathbf{y}=\mathbf{X}\mathbf{\beta }+\mathbf{\epsilon }$$
其中标签或响应变量为$\mathbf{y}\equiv {\left(y_1{y}_2\cdots y_n\right)}^{\prime }$；$\mathbf{X}$为变量向量，$\mathbf{\beta }$是参数向量，$\mathbf{\epsilon }$是残差向量。为估计参数向量$\mathbf{\beta }$，使用普通最小二乘法OLS得
$$\underset{\mathbf{\beta }}{\min }L(\mathbf{\beta })=\underset{SSR}{\underbrace{(\mathbf{y}-\mathbf{X}\mathbf{\beta }{)}^{\prime }(\mathbf{y}-\mathbf{X}\mathbf{\beta })}}$$
求解得
$${\hat{\mathbf{\beta }}}_{OLS}\equiv {\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-1}{\mathbf{X}}^{\prime }\mathbf{y}$$
这里必须假设${\left({\mathbf{X}}^{\prime }\mathbf{X}\right)}^{-1}$存在。对于高维数据，OLS适应性下降，因此考虑对损失函数$L(\mathbf{\beta })$加以改进，加入$\mathbf{\beta }$的L2范数
$$\underset{\mathbf{\beta }}{\min }L(\mathbf{\beta })=\underset{SSR}{\underbrace{(\mathbf{y}-\mathbf{X}\mathbf{\beta }{)}^{\prime }(\mathbf{y}-\mathbf{X}\mathbf{\beta })}}+\underset{\text{penalty }}{\underbrace{\lambda \Vert \mathbf{\beta }{\Vert }_2^2}}$$
其中$\lambda$称为惩罚系数、调节系数或收缩因子；惩罚系数大，参数向量向原点越靠近。计入L2范数后，损失函数不仅要考虑预测误差平方和最小，也要兼顾参数向量的平方和大小：如果参数过大，那么损失函数不一定最小。上述$\mathbf{\beta }$的估计量即为${\mathbf{\beta }}_{ridge}$。同理，也可以加入$\mathbf{\beta }$的L1范数
$$\underset{\mathbf{\beta }}{\min }L(\mathbf{\beta })=\underset{SSR}{\underbrace{(\mathbf{y}-\mathbf{X}\mathbf{\beta }{)}^{\prime }(\mathbf{y}-\mathbf{X}\mathbf{\beta })}}+\underset{\text{penalty }}{\underbrace{\lambda \Vert \mathbf{\beta }{\Vert }_1}}$$
上述参数估计量称为${\mathbf{\beta }}_{lasso}$。将两种范数相结合
$$\underset{\mathbf{\beta }}{\min }(\mathbf{y}-\mathbf{X}\mathbf{\beta }{)}^{\prime }(\mathbf{y}-\mathbf{X}\mathbf{\beta })+\lambda \left[\alpha \Vert \mathbf{\beta }{\Vert }_1+(1-\alpha )\Vert \mathbf{\beta }{\Vert }_2^2\right]$$
其中$\lambda$为惩罚系数，$\alpha$为混合系数，即L1范数惩罚所占比例，$1-\alpha$为L2惩罚所占比例。$\alpha \in (0,1)$时，上述参数向量估计量即为弹性网估计量${\mathbf{\beta }}_{elasticnet}$。$\alpha =0$退化为ridge回归；$\alpha =1$退化为lasso回归。参数$\lambda$和$\alpha$通过交叉验证最小化均方误差获得。

---

3 弹性网估计

下面是Python代码

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import RidgeCV
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import ElasticNetCV
from sklearn.linear_model import enet_path
# 使用boston数据集
boston = pd.read_csv('boston.csv')
# 特征变量提取
X_raw = boston.iloc[:, :-1]
# 响应变量
y = boston.iloc[:, -1]
# 特征变量标准化
scaler = StandardScaler()
X = scaler.fit_transform(X_raw)
# 模型估计,惩罚系数任意(0,1)
# l1_ratio = 0表示岭回归，l1_ratio = l为套索回归;alpha惩罚系数
model = ElasticNet(alpha=0.1, l1_ratio=0.5)
model.fit(X, y)
print('模型得分：\n',model.score(X, y))
result = pd.DataFrame({'变量':X_raw.columns,'系数':model.coef_})
print(f'最优回归系数：\n',result)
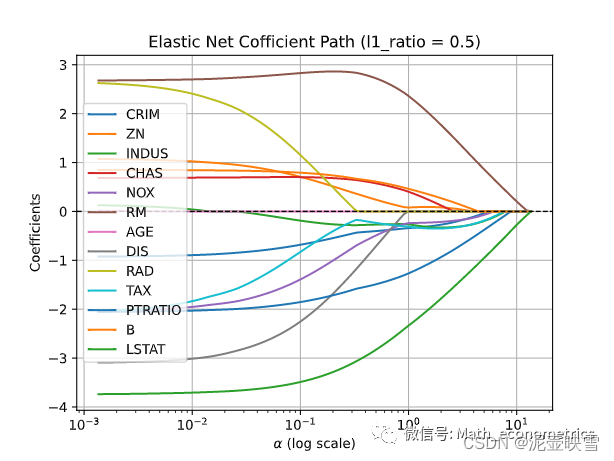
# 收缩路径
alphas, coefs, _ = enet_path(X, y, eps=1e-4, l1_ratio = 0.5)
ax = plt.gca()
ax.plot(alphas, coefs.T)
ax.set_xscale('log')
plt.xlabel(r'$\alpha$ (log scale)')
plt.ylabel('Coefficients')
plt.title('Elastic Net Cofficient Path (l1_ratio = 0.5)')
plt.axhline(0, linestyle='--', linewidth=1, color='k')
plt.legend(X_raw.columns)
plt.grid()
plt.show()

使用十折交叉验证惩罚参数和混合参数

#alpha = 0.001-1;lambda =  0.001-1
alphas = np.logspace(-3, 0, 100)
kfold = KFold(n_splits=10, shuffle=True, random_state=1)
model = ElasticNetCV(cv=kfold, alphas=alphas, l1_ratio=np.logspace(-3, 0, 100))
model.fit(X, y)
print('最优惩罚系数：\n',model.alpha_)
print('最优混合系数：\n',model.l1_ratio_)
# 最优惩罚系数：0.02848035868435802
#最优混合系数：1.0

混合系数$\alpha =1$,此时选择模型lasso回归，最优惩罚参数为$\lambda =0.028$

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=2344)
fit = Lasso(alpha=model.alpha_)
fit.fit(X_train, y_train)
score = model.score(X_train, y_train)
print('模型得分：',score)
result = pd.DataFrame({'变量':X_raw.columns,'系数':model.coef_})
print(f'回归系数：\n',result)
# 模型得分： 0.7237822155914061
# 回归系数：
#           变量        系数
# 0      CRIM -0.846146
# 1        ZN  0.965785
# 2     INDUS -0.000000
# 3      CHAS  0.680701
# 4       NOX -1.886944
# 5        RM  2.713469
# 6       AGE -0.000000
# 7       DIS -2.935723
# 8       RAD  2.203538
# 9       TAX -1.658672
# 10  PTRATIO -2.011514

---

-END-

陈强,《机器学习及Python应用》高等教育出版社, 2021年3月