932. 漂亮数组（中等）

在这里插入图片描述

解法一：分治法

重点

这里给出两个定理：

如果 X,Y,Z 是漂亮数组，则 k * X + b, k * Y + b, k * Z + b 一定也是漂亮数组；
奇数 + 偶数 = 奇数。

因此不难证明，如果 2 * Y ≠ X + Z，则 2 * k * Y + b ≠ k * X + b + k * Z + b 一定成立。

思路

对于一个正整数 N ，我们寻找中点将其等分成两部分 ，left 和 right ，如果 left 和 right 都是漂亮数组，同时 left 部分全部是奇数 ， right 部分全部是偶数 ，那么left + right 组成的数组一定也是漂亮数组 。

因此，可以采用分治算法，自顶向下逐步分解，先找到 N 的中点，通过 (N+1)/2 和 N/2 将数组分成左右两部分。其中，奇数全部放在 left ，偶数全部放在 right ，同时保证 left 和 right 都是漂亮数组，然后一步一步进行分解。

直到 N = 1 时，数组中只有一个元素 [1] ，不需要再进行分解。

接下来，我们从底层部分考虑合并。如果我们知道了整数 N 的漂亮数组，那么可以通过 k * N + b 的变换使得 N 变为 2N 的奇数部分（left），同样地，可以通过变换使得 N 变为 2N 的偶数部分（right）。

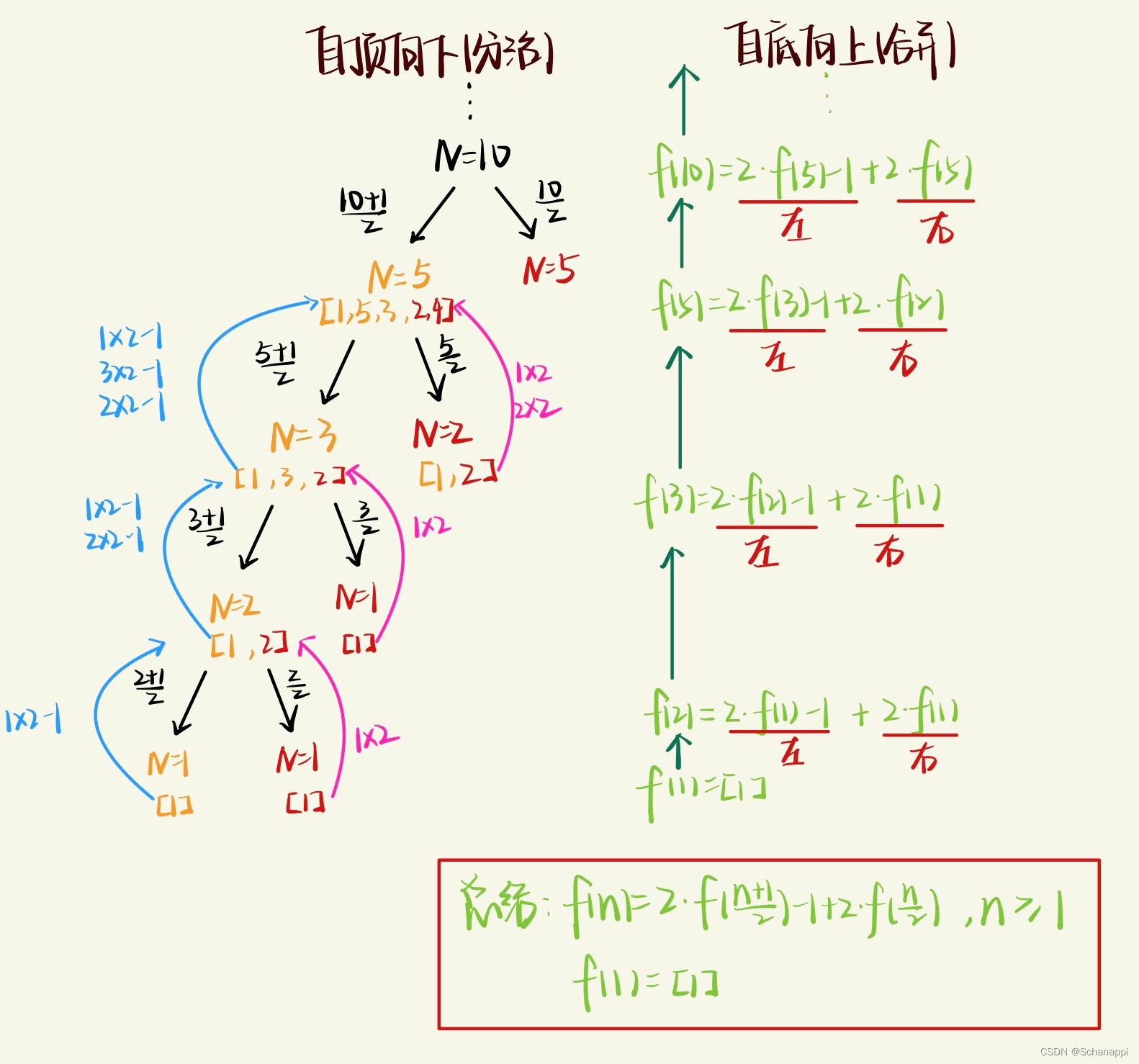
下面的图展示了一个完整的分析过程。

首先自顶向下进行考虑，找到 N 的中点，通过 (N+1)/2 和 N/2 不断将数组分成左右两部分；
直到 N = 1，我们可以返回 N = 1 的漂亮数组为 [1] ；
最后考虑自底向上的合并 ，即对 left 中的每一个元素进行 left[i] * 2 -1 ，得到更高一级数组的左半部分，对 right 中的每一个元素进行 right[i] * 2 ，得到更高一级数组的右半部分。

在这里插入图片描述

代码

class Solution {
public:
    vector<int> beautifulArray(int n) {
        // if(n == 1) return {[1]};
        vector<int> ans, left, right;
        if(n > 1){
            left = beautifulArray((n+1)/2);
            right = beautifulArray(n/2);
            for(int l : left){
                ans.push_back(l * 2 - 1);
            }
            for(int r : right){
                ans.push_back(r * 2);
            }
        }
        else ans.push_back(1);
        return ans;
    }
};

解法二：分治法 + 记忆化搜索

以 N = 10 为例，第一步是分解成 N = 5 和 N = 5 两部分，如果按照解法一，需要计算两次 N = 5 的漂亮数组。显然产生了重复计算，因此我们可以在第一次计算出 N = 5 的漂亮数组时，使用 mp 将答案保存下来，第二次遍历时只需要在 mp 查找即可，减少了时间复杂度。

代码

class Solution {
public:
    unordered_map<int, vector<int>> mp;
    vector<int> beautifulArray(int n) {
        // 判断n是否已经计算过
        if(mp.find(n) != mp.end()){
            return mp.find(n) -> second;
        }
        vector<int> ans, left, right;
        if(n > 1){
            left = beautifulArray((n+1)/2);
            right = beautifulArray(n/2);
            for(int l : left){
                ans.push_back(l * 2 - 1);
            }
            for(int r : right){
                ans.push_back(r * 2);
            }
        }
        else ans.push_back(1);
        mp[n] = ans;
        return ans;
    }
};

解法三：动态规划

其实弄明白解法一之后，动态规划的思路就变得很简单。

动态规划的思想，就等同于「分治法」中的合并，即自底向上的考虑。

我们从 N = 1 的漂亮数组开始，找到 N = 2 的漂亮数组，找到 N = 3 的漂亮数组…直到计算出 N = n 的漂亮数组。

状态定义

因此，我们很容易就能完成状态定义，令 dp[i] 表示长度为 i 的漂亮数组。

状态转移方程

我们通过解法一的分析图不难发现，dp[i] 由两部分组成：2 * dp[(i+1)/2] - 1 和 dp[i/2] * 2 ，因此遍历 dp[(i+1)/2] 和 dp[i/2] ，并对它们的元素做相应变换，依次存入 dp[i] 即可。

初始化

我们令 dp[1] = {1} ， N = 2 的漂亮数组可以由 N = 1 变换得到。

返回的最终结果

最终返回 dp[n] ，表示 N = n 的漂亮数组。

代码

class Solution {
public:
    unordered_map<int, vector<int>> mp;
    vector<int> beautifulArray(int n) {
        vector<vector<int>> dp(n+1);
        
        // 初始化
        dp[1].push_back(1);

        // 状态转移
        for(int i=2; i<=n; ++i){
            for(int l : dp[(i+1)/2]){
                dp[i].push_back(l * 2 - 1);
            }
            for(int r : dp[i/2]){
                dp[i].push_back(r * 2);
            }
        }
        return dp[n];
    }
};