前言

人们常说，大脑是人类已知的最复杂的网络。人类大脑由大约1000亿个(1011个)神经元组成，由大约100万亿个(1014个)突触连接，这些神经元在多个空间尺度上进行组织，在多个时间尺度上进行功能交互。这个庞大的系统是我们所有思想、感觉和行为的生物硬件。人类大脑网络的相关疾病，如痴呆和精神分裂症，是全球健康问题之一。因此，理解脑网络的连接一直是神经科学的核心目标。

目前关于大脑网络的核心思想是连接组的概念。这个词是由Olaf Sporns、Giulio Tononi和Rolf Kotter(2005)首次提出，并在Patric Hagmann(2005)的博士论文中独立提出，用来定义一个矩阵，表示大脑神经元之间所有可能的成对解剖连接(图1)。从最严格的意义上来说，“连接组”这一词代表了关于大脑细胞连接图的理想或规范状态。近年来，该领域的研究呈指数级增长，包括大规模脑区之间以及单个神经元之间的解剖连接矩阵、通过分析生理过程揭示的功能连接矩阵。对跨空间和时间尺度的脑网络组织进行量化、可视化是连接组学领域的一个基本特征。

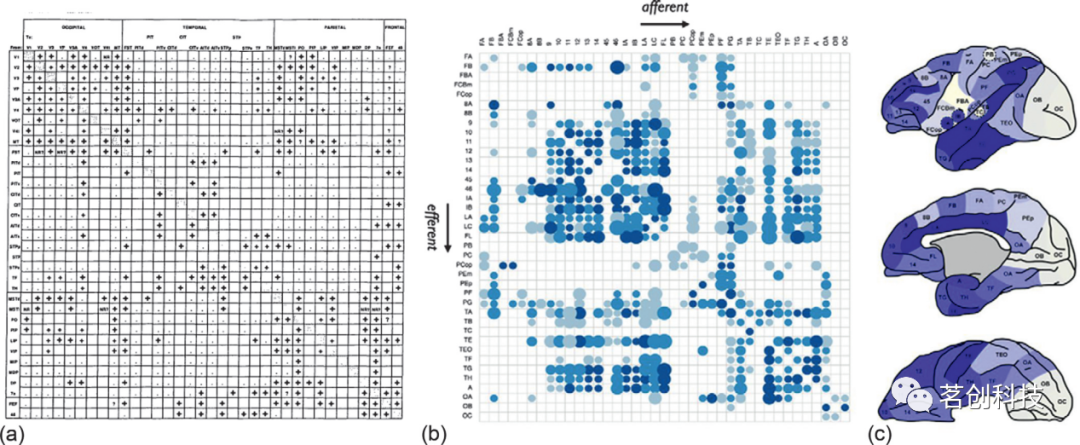
图1.连接组矩阵。矩阵中的点大小与投影距离成正比，颜色越深表示连接强度越强，(c)中颜色较深的区域表示该区域与网络其余部分总体连接较高。

连接组学的诞生相对较晚，但有两个趋同因素推动了连接组学发展的科学优势。首先，近年来网络科学总体上发展迅速。自20世纪80年代以来，复杂网络的统计物理学在概念上取得了重大进展，网络科学在大数据分析和建模方面的应用也越来越广泛，而且人们已经找到了量化拓扑复杂性的新方法。其次是跨多个分辨率尺度测量和可视化大脑组织方法上的技术进步。自20世纪90年代以来，人类神经影像科学取得了重大进展，特别是使用MRI在宏观尺度上绘制健康被试和神经精神疾病患者的全脑解剖和功能网络。过去十年中，在纤维束追踪、光学显微镜、光遗传学、多电极记录、组织学基因表达和许多其他神经科学技术方面也有了惊人的进展，这些技术可用于在更可控的实验条件以及更广泛的物种范围内绘制介观(~10-4m)和微观尺度(~10-6m)大脑系统。

这两个强大趋势的融合：①复杂网络科学的数学和概念发展；②测量神经系统技术的发展——是推动连接组学发展的关键，也是这一领域的显著特征。本文是关于我们如何应用复杂网络科学来理解大脑连接，着重于使用图论来建模、估计和模拟脑网络的拓扑结构与动态。图论是数学的一个分支，涉及理解相互作用元素的系统。图用于将这种系统简单地建模为由边连接的一组节点。这种表示非常灵活，尽管形式简单，但可用于研究不同类型数据中大脑组织的许多方面。

图论简史

瑞士数学家莱昂哈德·欧拉(Leonhard Euler)首次使用图形来理解现实世界系统。1735年，欧拉住在普鲁士的哥尼斯堡镇(现在的俄罗斯加里宁格勒)，普雷格尔河流经此镇，共有七座桥横跨普雷格尔河，连接着两大主要河岸和河中央的两个岛屿(图2a)。当时一个悬而未决的问题是，怎样将每座桥恰好走过一遍并回到出发点。欧拉解决这个问题的方法是，将河流划分的四块陆地表示为节点，将七座桥梁表示为相互连接的边(图2b)。从这个原型图中，他能够证明，要使漫步成为可能，连接到图其余部分的边的数量不超过两个节点，这样才能恰好把每座桥都走一遍并回到出发点。事实上，哥尼斯堡图中的四个节点的边数都是奇数，这意味着不可能找到每座桥都只经过一次的饶镇路线。通过这种方式，欧拉彻底证明了组成城镇的桥梁和岛屿系统的组织方式：“哥尼斯堡步行”在拓扑结构上是禁止的。

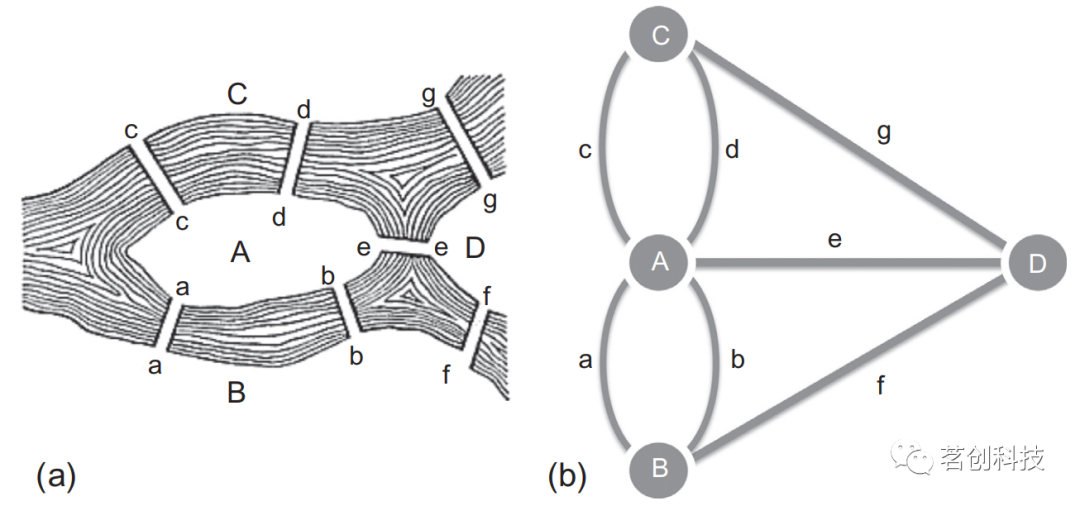
图2.图论的起源：欧拉的第一个拓扑分析。

欧拉分析的重要性不在于18世纪哥尼斯堡的地理细节；相反，它之所以重要，正是因为它将注意力集中在后来被称为拓扑结构的问题上。图的拓扑定义了系统元素之间的链接是如何组织的。拓扑学作为数学的一个领域，从19世纪晚期开始迅速发展。20世纪50年代，Paul Erdős和Alfred Rényi提出了一个很有影响力的统计模型，用于生成随机图并预测它们的一些拓扑属性。在Paul-Erdős图中，有N个节点，它们之间每条可能边的均匀概率为p。如果p接近于1，则图是密集连接的；如果p接近于0，则图是稀疏连接的。Erdős和Rényi表明，这些图的许多重要属性，例如连接到任何单个节点上的平均连接数(也称为图的平均度)，以及图是单个连接组件还是包含孤立节点(不与其他节点连接)，都可以从他们的生成模型中进行分析预测。

欧拉提出的哥尼斯堡图和Erdős-Rényi模型生成的随机图都是最简单的图类，即二值无向图。它们之所以是二值图，是因为边要么不存在，要么存在，或者说，边的权重要么为0，要么为1。它们是无向图，因为边对称地连接节点，连接的源和目标之间没有区别。拓扑分析的原理后来被扩展到更复杂的图中，包括加权连接和有向连接，这些扩展对于表征某些类型的脑网络数据特别重要。

Duncan Watts和Steven Strogatz迈出了从随机图论数学到复杂网络物理学的关键一步。像Erdős和Rényi一样，他们定义了图形的生成模型，但他们从N个节点的简单规则网开始分析，每个节点直接连接到任意数量的其他节点。然后Watts-Strogatz模型随机选择一条连接格中节点i和j的边，并增量地重连图形，使这条边将节点i连接到另一个随机选择的节点h，h≠j。这种连接随机突变的生成过程可以应用于每条边，以任意概率重连pWS，因此当pWS=1时，所有边被随机重连，网格被拓扑转换为一个Erdős-Rényi随机图。

Watts和Strogatz(1998)重点研究了其网络模型的两个关键属性：聚类系数和特征路径长度。聚类系数是用来描述图中顶点之间集成团程度的指标，是一个点的邻接点之间相互连接的程度。特征路径长度通常用于衡量网络的总体效率，是节点之间拓扑距离的度量，计算为连接网络中任意两个节点所需的最小边数。直观上看，较短的平均路径长度会使整个网络的集成更快速和有效。随机图具有特征路径短、聚类性低的特点。另一方面，Watts和Strogatz分析的规则网具有高聚类性和长特征路径长度(图3)。

图3.小世界网络。

Watts-Strogatz模型的计算机模拟揭示的第一个关键发现是，路径长度的变化率比聚类的变化率快得多，因为在网格中重连边的概率从0到1逐渐增加。具体来说，仅改变网格上的几条边就可以显著地降低图的特征路径长度，但并没有显著减少网格上的高平均聚类。换句话说，有一系列的重连概率生成具有混合拓扑属性的图：短路径长度，如随机图；高聚类，如网格。与Milgram(1967)首先研究的社交网络的性质类似，这些近乎规则和近乎随机的图被称为小世界网络(small-world networks)。Watts和Strogatz报告的第二个主要发现是基于实证分析。他们测量了代表三个现实生活系统的图的路径长度和聚类，发现大于随机的聚类和几乎随机的路径长度的小世界组合是这三个系统的特征：社会网络(联合主演的电影演员)，基础设施网络(电网)，线虫的神经网络(秀丽隐杆线虫)。

与此同时，Barabasi和Albert(1999)提出了另一个生成模型，该模型通过增量地添加节点来构建复杂图。在这个模型中，当每个新节点i被添加到图中时，它与任何其他节点j形成连接或边的概率与节点j的连接数量或程度成正比。换句话说，新节点优先连接到已经有大量连接的现有节点，从而表示假定的网络枢纽。通过这种择优连接的生成过程，“富人越富”，或者随着图的迭代增加新节点，最初具有高度数的节点往往具有更高的度。因此，网络节点的度分布并非Erdős-Rényi模型所特有的单峰类泊松分布；相反，它是典型的厚尾分布，符合所谓的无标度网络或幂律分布。无标度分布意味着在图中找到一个非常高的度枢纽节点的概率比在度分布为单峰(如泊松函数或高斯函数)时的预期概率要大。更简单地说，无标度网络可能至少包含几个高度连接的枢纽节点。

将图论应用于现实世界系统的第三个主要进展是发现了这种网络是模块化的——它们几乎可以分解为节点子集，这些节点之间的连接比任何其他模块中的节点连接更为紧密。网络模块化的量化已经成为复杂网络科学中一个庞大且迅速发展的领域。在拓扑模块化较高的网络中，模块内连接的密度远大于模块间连接的密度。通常，大多数模块间的通信是由一些连接不同模块的连接枢纽进行介导的。事实证明，许多现实生活中的系统共享这种模块化的拓扑属性，再次表明它代表了复杂网络的一种近乎普遍的特征。

图论与大脑

正如我们所看到的，图论在理解复杂系统的结构和功能方面发挥了不可或缺的作用。神经系统无疑是复杂的，因此可以很自然地假设图论对神经科学也是有用的。重要的是，基于图的脑网络表征(即脑图)可以很容易地从神经连接矩阵中构建出来，如图1所示。矩阵中代表不同脑区的每一行或每一列都被绘制为图中的一个节点，每个矩阵元素中的值被绘制为边。事实上，网络的矩阵和图表征在形式上是等价的。接下来，本文将阐述如何应用图论来理解大脑网络，以及图论如何成为连接组学的强大分析工具。

微观尺度下的神经元学说和连通性

图论和网络科学的思想是什么时候开始渗透到神经科学的？正式地说，图论在神经科学数据上的首次应用直到20世纪末才发表。然而，在19世纪末和20世纪初，由Ramón y Cajal杰出的微观研究和理论思考所建立的开创性神经元理论，为图论作为神经系统的模型奠定了基础(图4)。

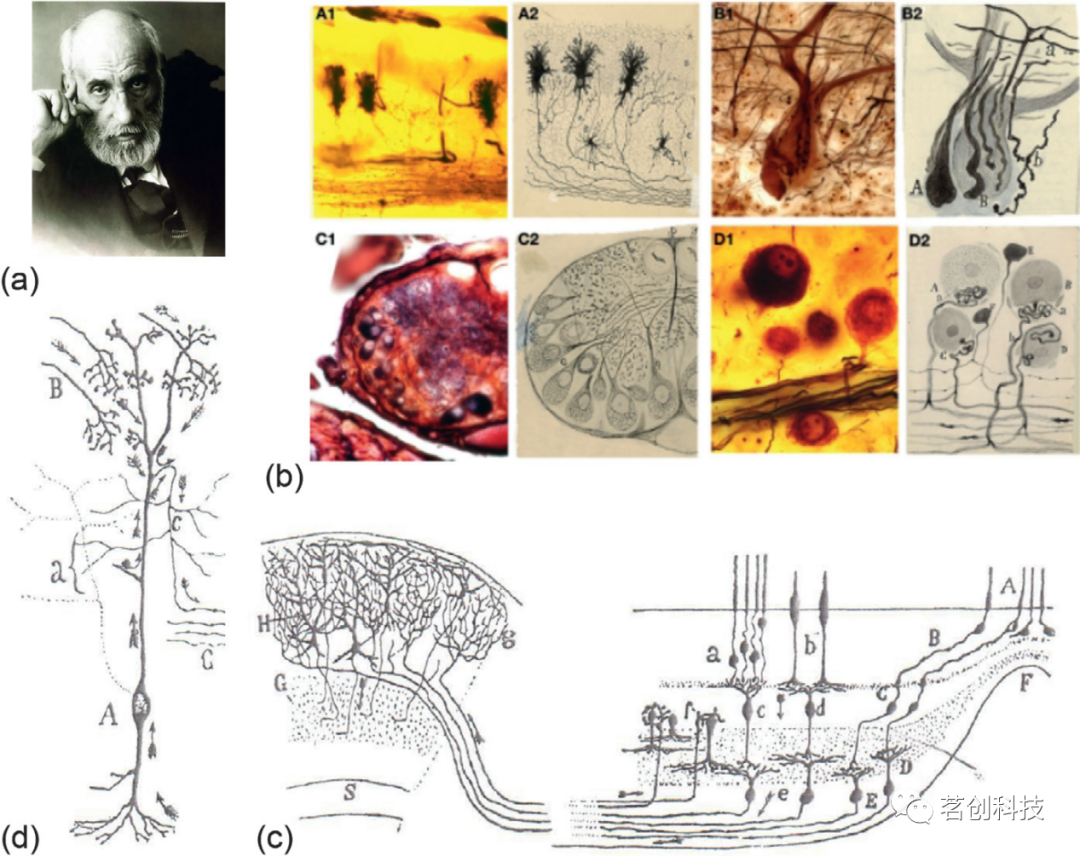
图4.Ramón y Cajal的开创性工作。

Ramón y Cajal的由突触连接的离散神经元模型自然适合于图论表征，其中神经元由节点表示，轴突投射或突触连接由边表示。Ramón y Cajal预计，大脑网络组织的许多方面将由最小化轴突连接成本来驱动，从而节省了细胞材料和空间，以及通过最小化神经元之间信息传递的传导延迟来节省时间。事实证明，大脑网络组织的许多方面似乎确实被选择来最小化布线成本或最小化代谢消耗。像模块和团簇等拓扑特征通常在解剖学上是共区域化的，这节省了材料。连接组的其他方面可以促进整个网络中信息的有效整合，例如较短的特征路径长度可能被选择来最小化传导延迟，从而提高神经元之间的信息交换速度或节省了时间。

宏观尺度下的临床病理学相关性和连通性

对相互连接的皮层区域的宏观网络研究大致与Ramón y Cajal关于微观神经元连接的开创性工作类似。网络图是由Theodor Meynert、Carl Wernicke和Ludwig Lichtheim等临床先驱绘制的，用来总结皮层区域之间的白质连接，并解释大脑紊乱的症状如何与病理病变相关。Wernicke-Lichtheim语言模型仍然是这些早期的宏观脑网络组织模型中最成功的，它将额叶皮层的语言产生区与颞叶皮层的语言理解区联系起来。该模型的某些方面能够令人信服地解释特定症状的产生：特别是，连接额叶和颞叶语言区域的弓状纤维束损伤，这被证明会导致患者无法重复所听到的单词，即所谓的传导性失语症(图5a)。这些先驱绘制的大规模脑网络组织图，包括一些由白质束(边)连接的空间限定区域(节点)，为宏观尺度上的神经系统图论分析奠定了基础。

图5.基于临床病理相关性的早期脑图。

宏观图表制作者(如Wernicke和Lichtheim)与微观解剖学家(尤其是Ramón y Cajal)之间的一个重要区别是他们所能获得的数据质量不同。得益于当代光学和组织染色技术的发展，Ramón y Cajal、Golgi等人能够制作出非常详细、高质量的神经元和显微电路图像(图4)。相比之下，宏观图表制作者使用的数据质量较差。例如，Wernicke的工作是基于临床病理学相关性，将临床中少数患者表现出的症状和体征模式与他们死后的大脑外观联系起来。即使在当时，这种方法和随后的诊断公式的不可靠性也受到了包括西格蒙德·弗洛伊德在内的同时代人的尖锐批评(图5b)。

Norman Geschwind、Marsel Mesulam及其同事在20世纪60年代和随后几年进行的断开或连接障碍综合征的研究，使更加整合的、基于网络的大脑模型得到了重新发展。这项工作表明，临床上观察到的许多心理缺陷可以用大脑的网络解剖来解释。它还表明，正常功能往往不是局限于一个单一的、专门的皮层区域，而是在解剖学上由一个大规模的网络来表示；例如，空间注意与由白质束连接的额、顶叶皮层区域以及皮层下核团的分布式集合有关(图5c)。从这个角度来看，损伤这些网络任何组成部分的病变或其他疾病过程可能与患者的症状障碍有关。随着将皮层解剖与心理功能和临床症状联系起来的高质量数据的获得，19世纪首次提出的大规模网络对于理解脑功能和脑障碍的重要性在大约100年后得到了肯定。

神经成像和人类连接组学

自20世纪80年代以来，人们对观察在两个不同解剖位置同时记录的成对神经生理时间序列之间的相互作用越来越感兴趣。最简单的分析方法是估计两个时间序列之间的相关系数：显示出信号随时间变化相关的脑区被认为是功能连接的。更正式地说，功能连接是指测量的神经生理信号时间序列之间的统计依赖性。这个概念最初是为分析单个单元记录的脉冲序列而开发的，然后由Karl Friston、Barry Horwitz、Randy McIntosh等人将其转化为对人类功能神经成像数据的分析。如果两个位置具有动态同步，那么可以说这两个位置是功能连接的，这一概念可以推广到许多不同的神经生理成像模式，包括功能磁共振成像(fMRI)、脑电图(EEG)、脑磁图(MEG)、记录局部场电位的多电极阵列(MEA)以及正电子发射断层扫描(PET)。

人脑功能网络的第一个图论分析是基于fMRI和M/EEG数据估计的功能连接矩阵。在这项工作中，对每一对可能的节点估计了在不同大脑位置记录的时间序列之间的相关性或相干性，并任意阈值化成对的相关性，以定义构成大规模功能网络图的二值边(图6a)。这项工作表明，人脑功能连接网络显示出与猕猴、猫和秀丽隐杆线虫的解剖网络以及许多其他自然复杂系统相似的组织特性。例如，功能性MRI网络是小世界(small-world)，包含枢纽，具有分层模块化结构，并且似乎受到最小化布线成本压力的约束(图6b)。事实上，空间约束(布线成本最小化)和拓扑结构之间的权衡是人脑网络的一个突出和可遗传的特征。

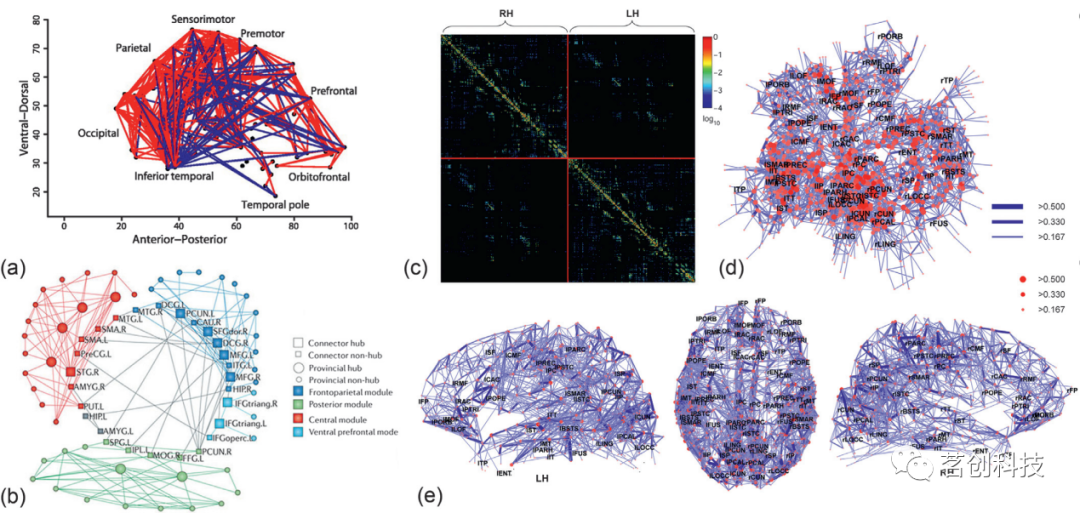
图6.来自人类磁共振成像(MRI)的脑图。

人脑解剖网络的首次图论分析是基于弥散MRI数据的示踪分析(图6c-e)和常规MRI数据的结构协方差分析。无论构建方法如何，人脑解剖网络具有与其他类型的脑网络同样重要的组织特性。虽然由神经束追踪、结构MRI、扩散MRI和功能MRI构建的脑图之间的融合令人鼓舞，但需要注意的是，功能连接和结构连接在许多方面是完全不同的概念。解剖学上的连接可以定义为从一个细胞到另一个细胞的轴突投射，或者在更大的空间尺度上，通过轴突束从一个区域投射到另一个区域。这种轴突投射预计只会随着时间缓慢变化。相比之下，功能连接是同步活动的统计指标，并不一定存在着潜在的解剖连接，而且可以随着时间快速变化。

小结

从Ramón y Cajal和Golgi等先行者第一次通过显微镜观察神经元的形态及其过程开始，了解大脑连接的重要性就显而易见了。然而，由于缺乏适当的工具和概念框架来测量、映射和模拟大规模神经元网络，随后几年的进展相对较缓。但是在过去的几十年里，我们不仅在微观、介观和宏观尺度上绘制大脑连接方面取得了惊人的进步，而且在量化和生成此类复杂系统的连接拓扑结构方面也取得了前所未有的进步。这些发展与采集、管理和传播有关大脑连接的大规模数据方法技术进步，以及更普遍的复杂网络科学的诞生相吻合。特别是，图论已经成为一种强大的工具，用于发展对跨空间和时间尺度的脑网络组织的理解，并使我们能够了解连接组如何与更广泛的自然发生的复杂系统相关联。

参考文献（上下滑动查看）：

Sporns, O. , Tononi, G. , & Kotter, R. . (2005). The human connectome: a structural description of the human brain. PLoS Computational Biology, 1(4), e42.

Hagmann, P. , Wedeen, V. J. , Maeder, P. , Thiran, J. P. , & Meuli, R. A. . (2005). From Scalar DWI to DTI and Beyond: Advantages and Pitfalls of Increasingly Complex Techniques. Radiological Society of North America 2005 Scientific Assembly and Annual Meeting.

Watts, D. , & Strogatz, S. . (1998). Collective dynamics of 'small-world' networks. Nature, 393(6684), P.440-442.

Milgram, S. . (1967). The small world problem. Psychology today, 2(1).

Barabasi, A.L. and Albert, R. (1999). Emergence of Scaling in Random Network. Science, 286, 509-512.

Stahnisch, F. W. , & Nitsch, R. . (2002). Santiago ramón y cajal's concept of neuronal plasticity: the ambiguity lives on. Trends in Neuroences, 25(11), 589-591.

Hux, K. . (2011). Wernicke–lichtheim model of aphasia. Springer New York.

Whitaker, H. A. , & Etlinger, S. C. . (1993). Theodor meynert's contribution to classical 19th century aphasia studies. Brain & Language, 45(4), 560-71.

Mesulam, M. M. , Hoesen, G. W. V. , Pandya, D. N. , & Geschwind, N. . (1977). Limbic and sensory connections of the inferior parietal lobule (area pg) in the rhesus monkey: a study with a new method for horseradish peroxidase histochemistry. Brain Research, 136(3), 393-414.

Lucy Lee, Karl Friston, & Barry Horwitz. . (2006). Large-scale neural models and dynamic causal modelling. NeuroImage, 30(4), 1243-1254.