目录

一、什么是ROC曲线

二、AUC面积

三、代码示例

1、二分类问题

2、多分类问题

---

一、什么是ROC曲线

我们通常说的ROC曲线的中文全称叫做接收者操作特征曲线（receiver operating characteristic curve），也被称为感受性曲线。

该曲线有两个维度，横轴为fpr（假正率），纵轴为tpr（真正率）

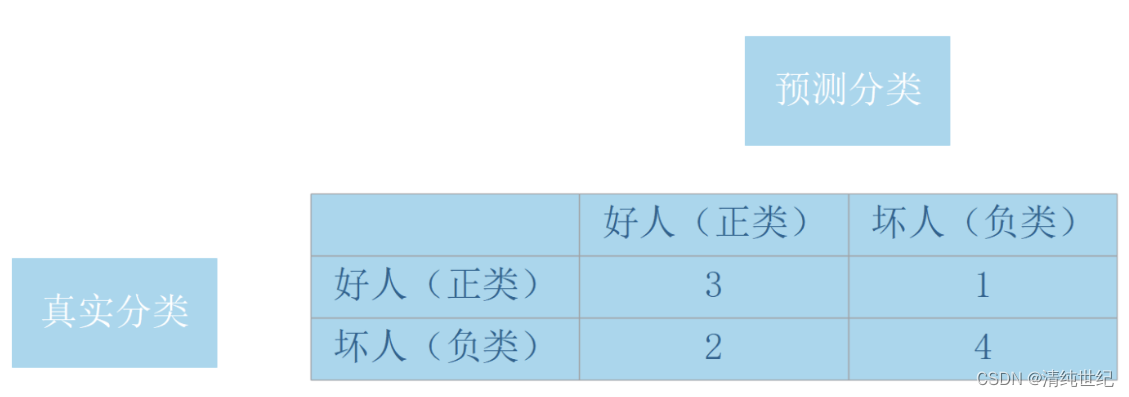
• 准确率（accuracy）：（TP+TN）/ ALL =（3+4）/ 10 准确率是所有预测为正确的样本除以总样本数，用以衡量模型对正负样本的识别能力。
• 错误率（error rate）：（FP+FN）/ ALL =（1+2）/ 10 错误率就是识别错误的样本除以总样本数。
• 假正率（fpr）：FP / (FP+TN) = 2 / （2+4）假正率就是真实负类中被预测为正类的样本数除以所有真实负类样本数。
• 真正率（tpr）：TP / （TP+FN）= 3 / （3+1）真正率就是真实正类中被预测为正类的样本数除以所有真实正类样本数。

• 这个曲线是怎么画出来的呢？

这幅曲线的每个点都对应一个（fpr，tpr），看过之前混淆矩阵的话，感觉一堆数据好像最终只能算出一个fpr和tpr，那是如何获得这么多的点的呢？

我们y会有一个预测为正类的概率，我们会将这个概率从大到小进行排序，然后再每个概率阈值的情况下进行将数据分类，能够计算出一组新的fpr和tpr，这样就会再不同的概率阈值下计算出多组点。

二、AUC面积

上面说了什么是ROC曲线，横轴为fpr，纵轴为tpr，fpr就是假正率，就是真实的负类被预测为正类的样本数除以所有真实的样本数，而tpr是真正率，是正式的正类被预测为正类的数目除以所有正类的样本数，所以我们的目标就是让假正率越小，真正率越大（负样本被误判的样本数越少，正样本被预测正确的样本数越大），那么对应图中ROC曲线来说，我们希望的是fpr越小，tpr越大，即曲线越靠近左上方越好，那么下面的面积也就成为了我们的衡量指标，俗称AUC（Area Under Curve）。

解释下图中四个点的含义：

• （0，0）：该点代表fpr和tpr都为0，也就是说此时负类样本全部预测正确，而正类样本全部预测错误。
• （0，1）：该点代表fpr为0，tpr为1，就是说此时负类样本全部预测正确，正类样本也全部预测正确，这也验证了我们上面说曲线越靠近左上方越好。
• （1，0）：该点代表fpr为1，tpr为0，即负类样本全部被预测为正类样本，而正类样本全部被预测为负类样本，这是最坏的情况，也就对应了图中的右下角。
• （1，1）：该点代表fpr为1，tpr为1，即负类样本全部预测错误，但是正类样本全部预测正确

y=x这条直线对应fpr和tpr是相等的，也就是我们模型评估正类和负类的能力是一样的，我们一般认为曲线要在该直线上方才有意义。

三、代码示例

下面是官方给出的示例，y代表着真实分类，scores代表着y对应的每个样本被预测为正类的概率，也就是说对于第一个样本来说，预测为2的概率为0.1，预测为1的概率为0.9，以此类推。

roc_curve(y_true,scores,pos_label): 对应的参数分别为y的真实标签，预测为正类的概率，pos_label 是指明哪个标签为正类，因为默认都是-1和1，1被当作正类，如果y对应的不是这个，就会报错，所以需要特别指明一下。

返回值为对应的fpr，tpr和thresholds

1、二分类问题

二分类示例：

from sklearn.metrics import roc_auc_score
from sklearn.metrics import roc_curve
from sklearn.metrics import auc
import numpy as np
 
y = np.array([1, 1, 2, 2])
scores = np.array([0.1, 0.4, 0.35, 0.8])
fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)

# 基于roc_curve函数返回fpr、tpr序列计算AUC的值（和roc_auc_score等价）
auc(fpr, tpr), roc_auc_score(y, pred)

注意：roc_curve只针对二分类情况，多分类情况有点特殊。下面给出多分类示例。

2、多分类问题

对于多分类问题，ROC曲线的获取主要有两种方法：

假设测试样本个数为m，类别个数为n。在训练完成后，计算出每个测试样本在各类别下的概率或置信度，得到一个[m， n]形状的矩阵P，每一行表示一个测试样本在各类别下概率值（按类别标签排序）。相应地，将每个测试样本的标签转换为类似二进制的形式，每个位置用来标记是否属于对应的类别（也按标签排序，这样才和前面对应），由此也可以获得一个[m， n]的标签矩阵L。

• 方法一：

每种类别下，都可以得到m个测试样本为该类别的概率（矩阵P中的列）。所以，根据概率矩阵P和标签矩阵L中对应的每一列，可以计算出各个阈值下的假正例率（FPR）和真正例率（TPR），从而绘制出一条ROC曲线。这样总共可以绘制出n条ROC曲线。最后对n条ROC曲线取平均，即可得到最终的ROC曲线。

• 方法二：

首先，对于一个测试样本：1）标签只由0和1组成，1的位置表明了它的类别（可对应二分类问题中的‘’正’’），0就表示其他类别（‘’负‘’）；2）要是分类器对该测试样本分类正确，则该样本标签中1对应的位置在概率矩阵P中的值是大于0对应的位置的概率值的。基于这两点，将标签矩阵L和概率矩阵P分别按行展开，转置后形成两列，这就得到了一个二分类的结果。所以，此方法经过计算后可以直接得到最终的ROC曲线。

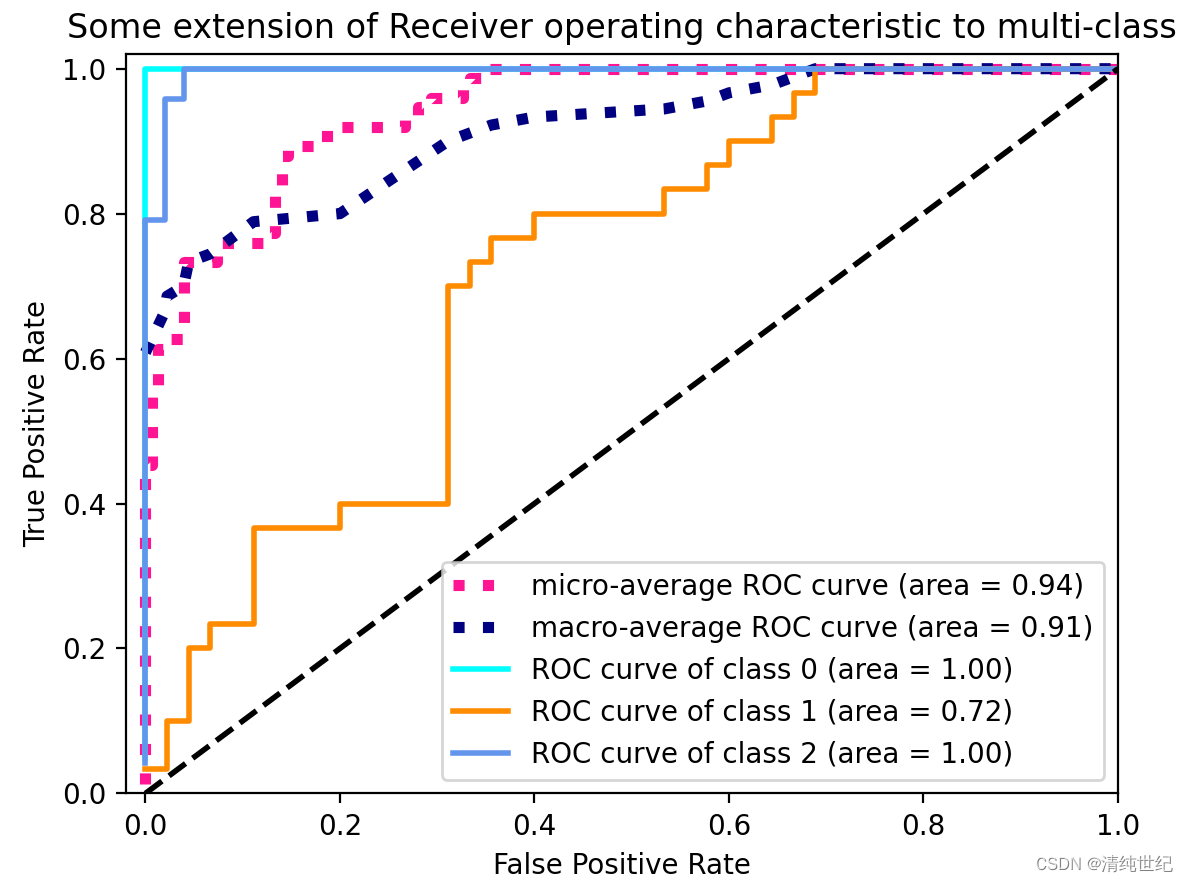
上面的两个方法得到的ROC曲线是不同的，当然曲线下的面积AUC也是不一样的。 在python中，方法1和方法2分别对应sklearn.metrics.roc_auc_score函数中参数average值为’macro’和’micro’的情况。下面参考sklearn官网提供的例子，对两种方法进行实现。

# 引入必要的库
import numpy as np
import matplotlib.pyplot as plt
from itertools import cycle
from sklearn import svm, datasets
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier
from scipy import interp

# 加载数据
iris = datasets.load_iris()
X = iris.data
y = iris.target

# 将标签二值化
y = label_binarize(y, classes=[0, 1, 2]) # 三个类别

# 设置种类
n_classes = y.shape[1]

# 训练模型并预测
random_state = np.random.RandomState(0)
n_samples, n_features = X.shape

# shuffle and split training and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.5,random_state=0)

# Learn to predict each class against the other
classifier = OneVsRestClassifier(svm.SVC(kernel='linear', probability=True,
                                 random_state=random_state))
y_score = classifier.fit(X_train, y_train).predict_proba(X_test) # 获得预测概率

# 计算每一类的ROC
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area（方法二）
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

# Compute macro-average ROC curve and ROC area（方法一）
# First aggregate all false positive rates
all_fpr = np.unique(np.concatenate([fpr[i] for i in range(n_classes)]))

# Then interpolate all ROC curves at this points
mean_tpr = np.zeros_like(all_fpr)
for i in range(n_classes):
    mean_tpr += interp(all_fpr, fpr[i], tpr[i])

# Finally average it and compute AUC
mean_tpr /= n_classes
fpr["macro"] = all_fpr
tpr["macro"] = mean_tpr
roc_auc["macro"] = auc(fpr["macro"], tpr["macro"])

# Plot all ROC curves
lw=2
plt.figure()
plt.plot(fpr["micro"], tpr["micro"],
         label='micro-average ROC curve (area = {0:0.2f})'
               ''.format(roc_auc["micro"]),
         color='deeppink', linestyle=':', linewidth=4)

plt.plot(fpr["macro"], tpr["macro"],
         label='macro-average ROC curve (area = {0:0.2f})'
               ''.format(roc_auc["macro"]),
         color='navy', linestyle=':', linewidth=4)

colors = cycle(['aqua', 'darkorange', 'cornflowerblue'])
for i, color in zip(range(n_classes), colors):
    plt.plot(fpr[i], tpr[i], color=color, lw=lw,
             label='ROC curve of class {0} (area = {1:0.2f})'
             ''.format(i, roc_auc[i]))

plt.plot([0, 1], [0, 1], 'k--', lw=lw)
plt.xlim([-0.02, 1.0])
plt.ylim([0.0, 1.02])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Some extension of Receiver operating characteristic to multi-class')
plt.legend(loc="lower right")
plt.show()