文章目录
- 二叉排序树(BST)
- 查找操作
- 二叉排序树的存储结构
- 查找实现
- 查找算法分析
- 二叉排序树的平均查找长度
- 插入操作
- 删除操作
- 代码实现
- 平衡二叉树(AVL)
- 插入&旋转操作
- 插入操作
- 四种旋转情况
- 代码实现
- 删除操作
- 查找操作
介绍
树表查找是一种在树形数据结构中进行查找的方法。与线性表查找不同,树表查找可以利用树形结构特性更搞笑地进行查找操作。在树表查找中,主要有二叉排序树、线索二叉树、红黑树、B树等实现方法。这些方法都是基于树形数据结构,但在实现和性能方面有所不同。
二叉排序树(BST)
二叉排序树(Binary Search Tree,BST),或是一颗空树,或者是具有下列特征的二叉树:
- 对于每个结点,其左子树上的所有结点的值均小于它的值。
- 对于每个结点,其右子树上的所有结点的值均大于它的值。
- 左、右子树也分别是一颗二叉排序树。
这个性质使得二叉排序树具有非常高的查找效率。
根据二叉排序树的定义,左子树结点值 < 根节点值 < 右子树结点值,因此对二叉树进行中序遍历,可以得到一个递增的有序序列。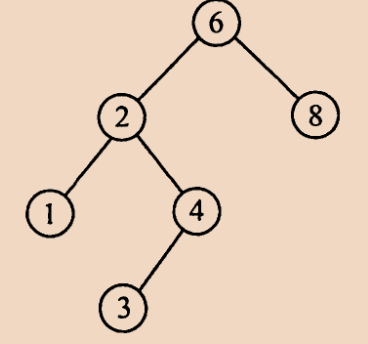
如图得到二叉排序树的中序遍历序列为 1 2 3 4 6 8
查找操作
二叉排序树的查找是从根节点开始,然后根据待查找值与当前结点值大小关系来决定沿着左子树查找还是右子树进行查找。显然这是一个递归的过程。
假设我们有以下二叉排序树:
8
/ \
3 10
/ \ \
1 6 14
/ \ /
4 7 13
查找值为7的节点:
- 从根节点8开始,7 < 8,沿着左子树;
- 接下来到节点3,7 > 3,沿着右子树;
- 到达节点6,7 > 6,沿着右子树;
- 最后到达节点7,查找成功。
二叉排序树的存储结构
定义二叉排序树:
typedef struct {
KeyType key; //关键字项
InfoType otherinfo; //其他数据域
};
typedef struct Node{
ElemType data;
struct Node* left;
struct Node* right;
}BSTNode *BSTree;
查找实现
递归算法:
递归算法实现简单,但其缺点是会消耗大量的栈空间,当树的深度非常大时,会出现栈溢出的情况。因此,递归算法更适合树比较小或者树高度较低的情况下使用。
BSTNode* BST_Search(BSTNode*T, ElemType data)
{
if(T == NULL || T->data == data ){
return T;
}
//递归查找
if(data<root->data)
{
return BST_Search(root->left,data);
}else{
return BST_Search(root->right,data);
}
}
二叉排序树的非递归查找算法:
非递归算法是一种迭代实现的方法,它通过栈或队列来保存未访问的结点,从而避免了递归算法消耗大量的栈空间问题。
非递归算法实现相对复杂一些,但却更加高效,尤其适合大规模树的查找操作。
BSTNode *BST_Search(BSTree T, ElemType key)
{
while(T!=NULL && key!=T->data)
{
if(key<T->data) T=T->left-child;
else T=T->right-child;
}
return T;
}
查找算法分析
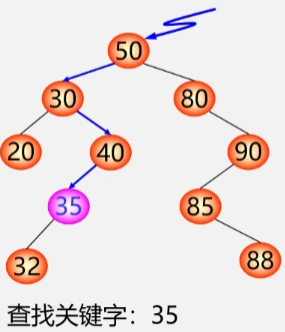
二叉排序树上查找某关键字等于给定值的结点过程,其实就是走了一条从根到该结点的路径。
- 比较的值的次数 = 此结点所在的层次数。
- 最多的比较次数 = 二叉排序树的深度。
二叉排序树的平均查找长度
在二叉排序树中,查找某个结点的平均查找长度(Average Search Length,ASL),是指所有结点所需的比较次数的平均值。平均查找长度是衡量二叉排序树查找性能的重要指标之一。
对于一个具有n个结点的二叉排序树,平均查找长度的计算公式如下:
ASL = ( 深度为1的结点数*1+深度为2的结点数*2+...+深度为h的结点数*h)/n
含有n个结点的二叉排序树的平均查找长度和树的形态有关。
- 树的高度越高,平均查找长度越长,反之越短。
- 最好的情况的树就是判定树
对于一颗平衡的二叉排序树,其深度为log n,因此平均查找长度为O(log n)。但如果二叉排序树退化为链表,其深度为n-1,此时平均查找长度为O(n)。因此,在实际应用中,为了保证较好的查找性能,应该尽可能保持二叉排序树的平衡。
提高形态不均匀的二叉排序树的查找效率
- 做平衡化(平衡二叉树)处理,尽量让二叉树的形态均衡
- 如果选择中间数作为根节点,可以保持树左右子树的相对平衡;
- 关键是根节点选哪个,如果选个小的,自然就有更多的元素跑到右子树,相对来说层次加深。
插入操作
实现步骤:
- 如果根节点为空,将新节点作为根节点;
- 如果根节点不为空,从根节点开始比较节点值与插入值的大小关系;
- 如果插入值小于当前节点值,将新节点插入到左子树中;
- 如果插入值大于当前节点值,将新节点插入到右子树中;
- 如果插入值等于当前节点值,则不插入重复节点;
- 插入节点后,需要保证二叉排序树的性质仍然成立,即对于任意节点,其左子树的值小于当前节点的值,右子树的值大于当前节点的值。
Node* insert(Node *root, int data) {
// 若根节点为空,创建一个新节点并返回
if (root == NULL) {
return createNode(data);
}
// 递归插入节点
if (data < root->data) {
root->left = insert(root->left, data);
} else {
root->right = insert(root->right, data);
}
return root;
}
其中createNode()函数用于在根节点为空时,创建一个根节点。
删除操作
删除操作不能把以该结点为根的子树上的结点都删除,必须先把被删除结点从存储二叉树的链表上摘下,将因删除结点而断开的二叉链表重新链接起来,同时确保二叉排序树的性质不会改变。
删除操作主要包括三种情况:
- 删除叶子结点:直接删除,不会破坏二叉排序树的性质
- 删除只有一个子树的结点:删除该结点,将其子树提升到被删除结点的位置。
- 删除有两个子树的结点:有两种方法实现。
- 寻找被删除节点的前驱节点(左子树中最大的节点),用前驱节点的值替换被删除节点的值,然后删除前驱节点。前驱节点要么是叶子节点,要么只有一个左子树。
- 寻找被删除节点的后继节点(右子树中最小的节点),用后继节点的值替换被删除节点的值,然后删除后继节点。后继节点要么是叶子节点,要么只有一个右子树。

如图,删除值为78的结点,并用后继节点替换它,在值为78的结点处进行中序遍历得到有序数列为 65 78 81 88 94 ,78的直接后继为81,所以用值为81的结点替换它。
TreeNode* findMin(TreeNode* root) {
while (root->left != NULL) {
root = root->left;
}
return root;
}
TreeNode* deleteNode(TreeNode* root, int key) {
if (root == NULL) {
return NULL;
}
if (key < root->val) {
root->left = deleteNode(root->left, key);
} else if (key > root->val) {
root->right = deleteNode(root->right, key);
} else {
// Case 1: 删除叶子节点
if (root->left == NULL && root->right == NULL) {
free(root);
root = NULL;
}
// Case 2: 删除只有一个子树的节点
else if (root->left == NULL) {
TreeNode* temp = root;
root = root->right;
free(temp);
} else if (root->right == NULL) {
TreeNode* temp = root;
root = root->left;
free(temp);
}
// Case 3: 删除有两个子树的节点
else {
TreeNode* temp = findMin(root->right);
root->val = temp->val;
root->right = deleteNode(root->right, temp->val);
}
}
return root;
}
代码实现
#include <stdio.h>
#include <stdlib.h>
// 定义二叉排序树节点结构体
typedef struct BSTNode {
int key; // 节点的值
struct BSTNode *left; // 左子节点
struct BSTNode *right; // 右子节点
} BSTNode;
// 创建新节点
BSTNode *newNode(int key) {
BSTNode *node = (BSTNode *)malloc(sizeof(BSTNode));
node->key = key;
node->left = NULL;
node->right = NULL;
return node;
}
// 向二叉排序树插入新节点
BSTNode *insert(BSTNode *root, int key) {
if (root == NULL) { // 如果根节点为空,创建新节点
return newNode(key);
}
if (key < root->key) { // 如果插入值小于根节点值,插入到左子树
root->left = insert(root->left, key);
} else if (key > root->key) { // 如果插入值大于根节点值,插入到右子树
root->right = insert(root->right, key);
}
return root;
}
// 寻找二叉排序树中的最小值节点
BSTNode *findMin(BSTNode *root) {
while (root->left != NULL) {
root = root->left;
}
return root;
}
// 从二叉排序树删除节点
BSTNode *deleteNode(BSTNode *root, int key) {
if (root == NULL) {
return root;
}
if (key < root->key) {
root->left = deleteNode(root->left, key);
} else if (key > root->key) {
root->right = deleteNode(root->right, key);
} else {
// 情况1:删除节点没有子节点
if (root->left == NULL && root->right == NULL) {
free(root);
root = NULL;
}
// 情况2:删除节点只有一个子节点(右子节点)
else if (root->left == NULL) {
BSTNode *temp = root->right;
free(root);
return temp;
}
// 情况3:删除节点只有一个子节点(左子节点)
else if (root->right == NULL) {
BSTNode *temp = root->left;
free(root);
return temp;
}
// 情况4:删除节点有两个子节点
else {
BSTNode *temp = findMin(root->right);
root->key = temp->key;
root->right = deleteNode(root->right, temp->key);
}
}
return root;
}
// 在二叉排序树中搜索指定值的节点
BSTNode *search(BSTNode *root, int key) {
if (root == NULL || root->key == key) {
return root;
}
if (key < root->key) {
return search(root->left, key);
} else {
return search(root->right, key);
}
}
// 更新二叉排序树中的节点值
BSTNode *updateNode(BSTNode *root, int oldKey, int newKey) {
// 先删除原来的节点
root = deleteNode(root, oldKey);
// 再插入新的节点
return insert(root, newKey);
}
// 中序遍历二叉排序树
void inorder(BSTNode *root) {
if (root != NULL) {
inorder(root->left);
printf("%d ", root->key);
inorder(root->right);
}
}
int main() {
BSTNode *root = NULL;
// 向二叉排序树插入节点
root = insert(root, 50);
root = insert(root, 30);
root = insert(root, 20);
root = insert(root, 40);
root = insert(root, 70);
root = insert(root, 60);
root = insert(root, 80);
// 打印二叉排序树
printf("Binary Search Tree: \n");
printf(" 50\n");
printf(" / \\\n");
printf("30 70\n");
printf(" \\ / \\ \n");
printf(" 40 60 80\n");
printf(" /\n");
printf("20\n\n");
// 删除节点 20
printf("Delete 20\n");
root = deleteNode(root, 20);
printf("Inorder traversal of the modified tree: \n");
inorder(root);
printf("\n\n");
// 删除节点 30
printf("Delete 30\n");
root = deleteNode(root, 30);
printf("Inorder traversal of the modified tree: \n");
inorder(root);
printf("\n\n");
// 删除节点 50
printf("Delete 50\n");
root = deleteNode(root, 50);
printf("Inorder traversal of the modified tree: \n");
inorder(root);
printf("\n\n");
// 更新节点 60 的值为 55
printf("Update 60 to 55\n");
root = updateNode(root, 60, 55);
printf("Inorder traversal of the modified tree: \n");
inorder(root);
printf("\n");
return 0;
}
平衡二叉树(AVL)
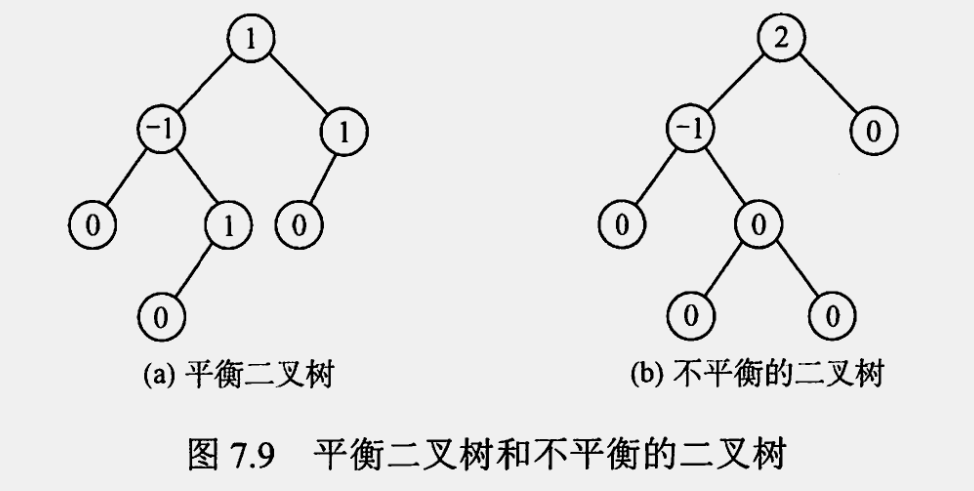
平衡二叉树(Balanced Binary Tree),AVL树,平衡二叉树的出现是为了避免树的高度增长过快,降低二叉排序树的性能,规定在插入和删除结点时,保证任意结点的左右子树高度差不超过1。
因此,平衡二叉树可定义为或者是一颗空树,或者是具有下列性质的二叉排序树:
- 它的左子树和右子树都是平衡二叉树
- 左右子树的高度差绝对值不超过1
为了方便起见,给每个结点附加一个数字,给出该结点左子树与右子树的高度差。这个数字成为结点的平衡因子(BF)。
- 平衡因子 = 左子树的高度 - 右子树的高度
- 平衡因子可以取三个值:-1 0 1 分别对应于左子树高度比右子树低一层、左右子树高度相等、左子树高度比右子树高一层。
- 平衡二叉树的定义中要求平衡因子的绝对值不超过 1。当平衡因子的绝对值超过 1 时,就需要通过旋转等操作来重新平衡二叉树,以保证其性质。
插入&旋转操作
二叉平衡树保证平衡的基本思想如下:每当在二叉平衡树中插入(或删除)一个结点时,首先检查其插入路径上的结点是否因为此次操作而导致了不平衡。若导致了不平衡,则先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A,再对以A为根的子树,在保证二叉平衡树的特性的前提下,调整各节点的位置关系,使之重新达到平衡。
注意:每次调整的对象都是最小不平衡子树,即以插入路径上离插入结点最近的平衡因子的绝对值大于1的结点作为根的子树。
插入操作
平衡二叉树的插入操作包括两个部分:插入新结点和平衡调整。
- 首先,将新结点插入到二叉排序树中的正确位置上,与普通的二叉排序树的插入操作一样。
- 然后,从新结点开始向上逐层更新每个结点的平衡因子,并检查是否导致了当前结点的不平衡。
- 如果当前结点的平衡因子绝对值大于1,则需要进行平衡调整。为了找到最小的平衡子树,我们需要在向上逐层更新平衡因子的过程中,记录下第一个平衡因子绝对值大于1的结点作为当前子树的根节点。
- 对以该根节点为根的子树进行平衡调整,可采用四种旋转操作之一。
- 最后,对于每个被更新了平衡因子的结点,需要检查其父节点的平衡因子是否需要更新,并进行相应的平衡调整,知道根节点为止。
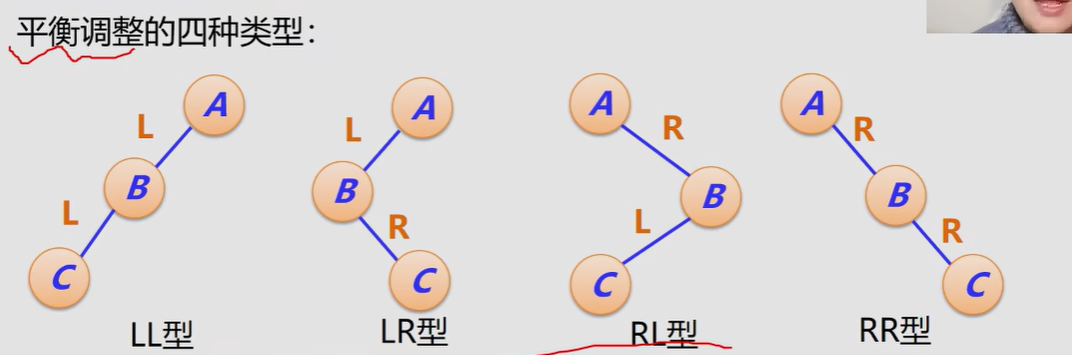
四种旋转情况
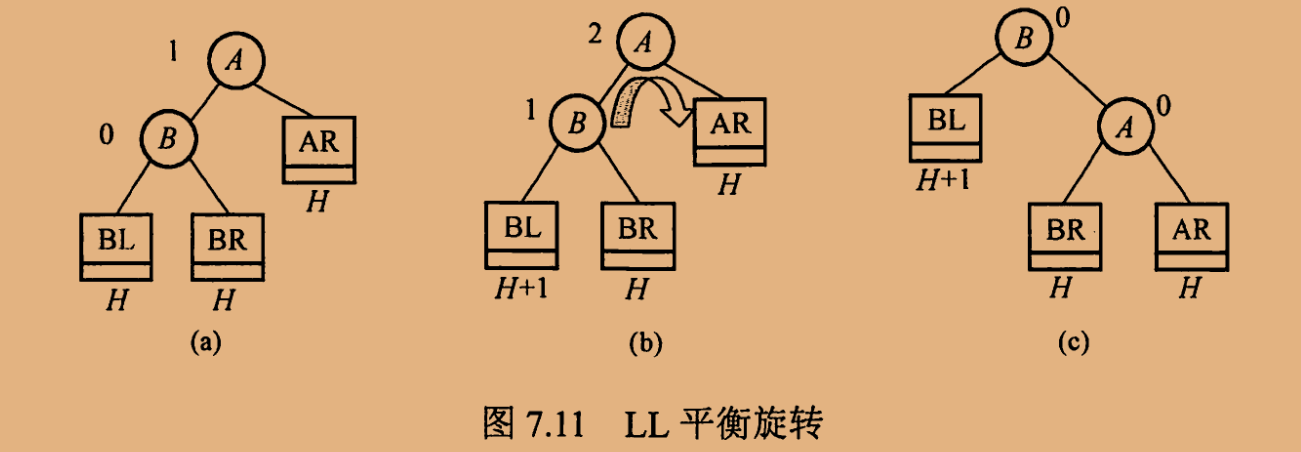
**1. LL平衡旋转(右单旋转) **
由于在结点A的做孩子(L)的左子树(L)上插入了新结点,A的平衡因子有1增至2,导致以A为根的子树失去平衡,需要一次向右的旋转操作。将A的左孩子B向右上旋转代替A成为根节点,将A结点向右下旋转成为B的右子树的根结点,而B的原右子树则作为A结点的左子树。
| |
A B
/ \ / \
B T3 -----> C A
/ \ / \
C T2 T2 T3
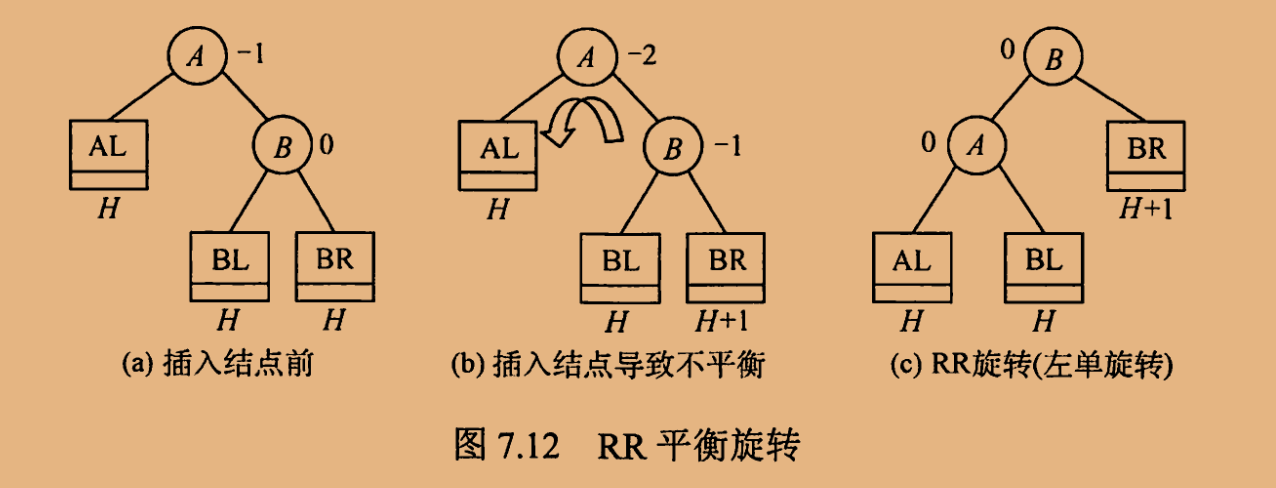
2. RR平衡旋转(左单旋转)
在 RR 旋转中,我们假设新结点插入在结点 A 的右孩子 B 的右子树®上。这时,结点 A 的平衡因子从 -1 变为 -2,导致以 A 为根节点的子树失去平衡。
为了恢复平衡,我们需要进行一次向左的旋转操作。具体来说,我们需要将结点 B 向左上旋转代替 A 成为根节点,将 A 结点向左下旋转成为 B 的左子树的根节点,而 B 的原左子树则作为 A 结点的右子树。
A(-1) B(0)
/ \ / \
T1 B(1) --> A(0) T3
/ \ / \
T2 T3 T1 T2
3. LR平衡旋转(先左后后双旋转)
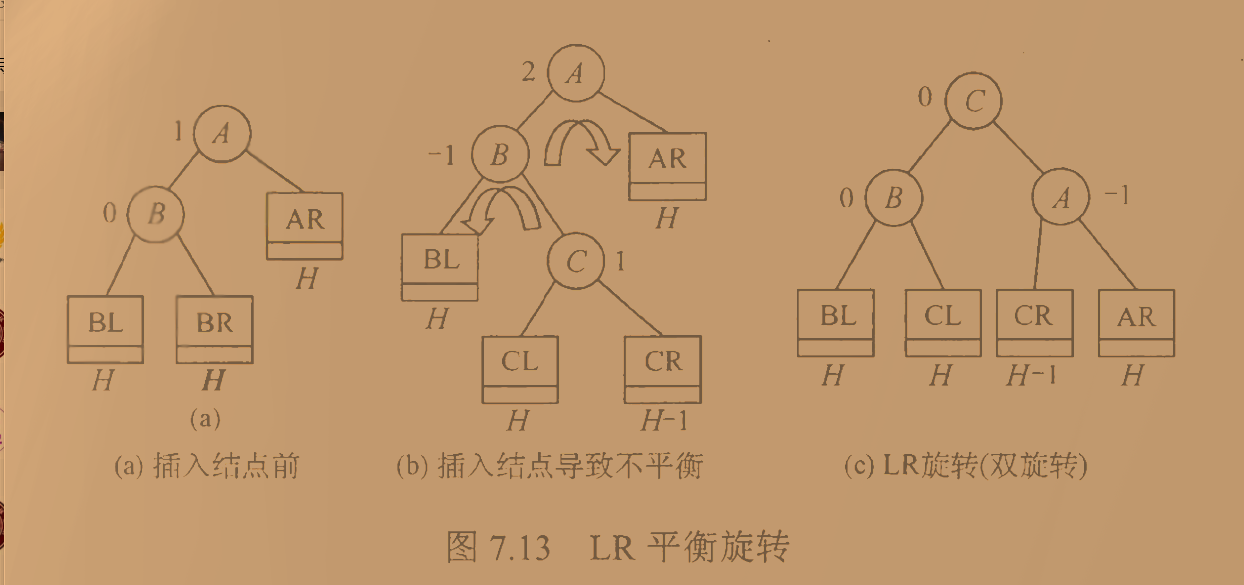
由于我们在A的左子树L的右子树R上插入新结点,导致A的平衡因子由1增至2,导致以A为根的子树失去平衡,此时需要进行两次旋转操作,先左旋转后右旋转。
第一次旋转将结点 B 的右子树 C 向左上旋转代替 B 成为根节点,将 B 向左下旋转成为 C 的左子树的根节点,而 C 的原左子树则作为 B 的右子树。
第二次旋转将结点 C 向右上旋转代替 A 成为根节点,将 A 向右下旋转成为 C 的右子树的根节点,而 C 的原右子树则作为 A 的左子树。
| | |
A(2) A(0) C(0)
/ \ / \ / \
B(0) T4 --> C(0) T4 --> B(-1) A(0)
/ \ / \ / \ / \
T1 C(1) B(-1) T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
4. RL 平衡旋转(先右后左双旋转)
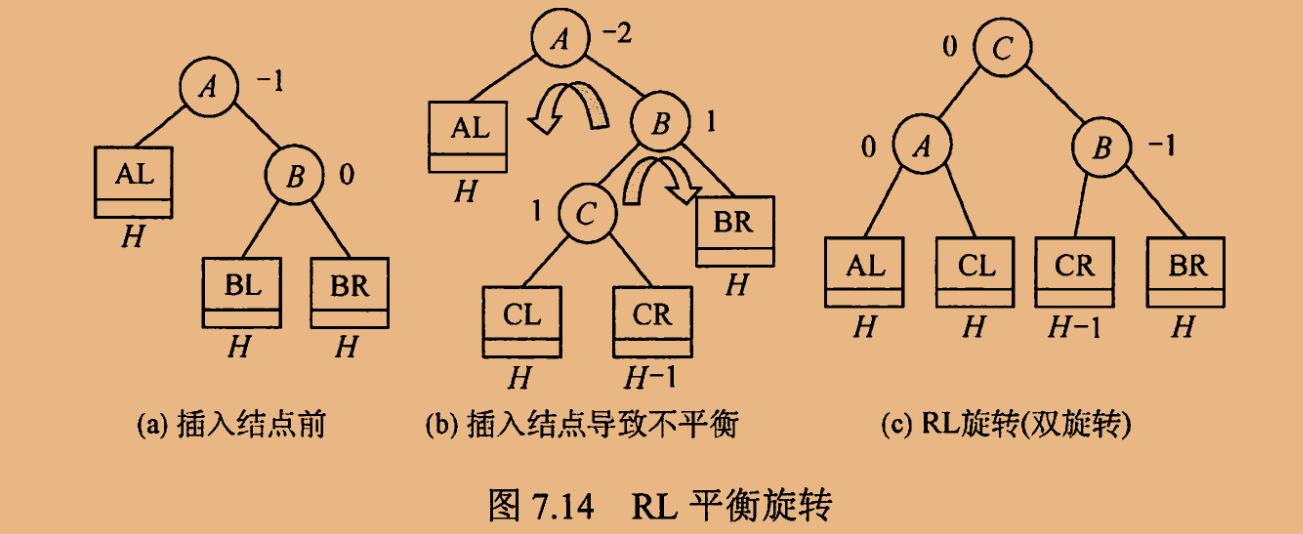
由于在A的右孩子®的左子树(L)上插入新结点, A的平衡因子由-1减至-2, 导致以A为根的子树失去平衡,需要进行两次旋转操作,先 右旋转后左旋转。
第一次旋转将结点 B 的左子树 C 向右上旋转代替 A 成为根节点,将 A 向右下旋转成为 C 的右子树的根节点,而 C 的原右子树则作为 A 的左子树。
第二次旋转将结点 C 向左上旋转代替 B 成为根节点,将 B 向左下旋转成为 C 的左子树的根节点,而 C 的原左子树则作为 B 的右子树。
| | |
A(-2) A(0) C(0)
/ \ / \ / \
T1 B(0) --> T1 C(0) --> A(0) B(1)
/ \ / \ / \ / \
C(-1) T4 T2 B(0) T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
例:
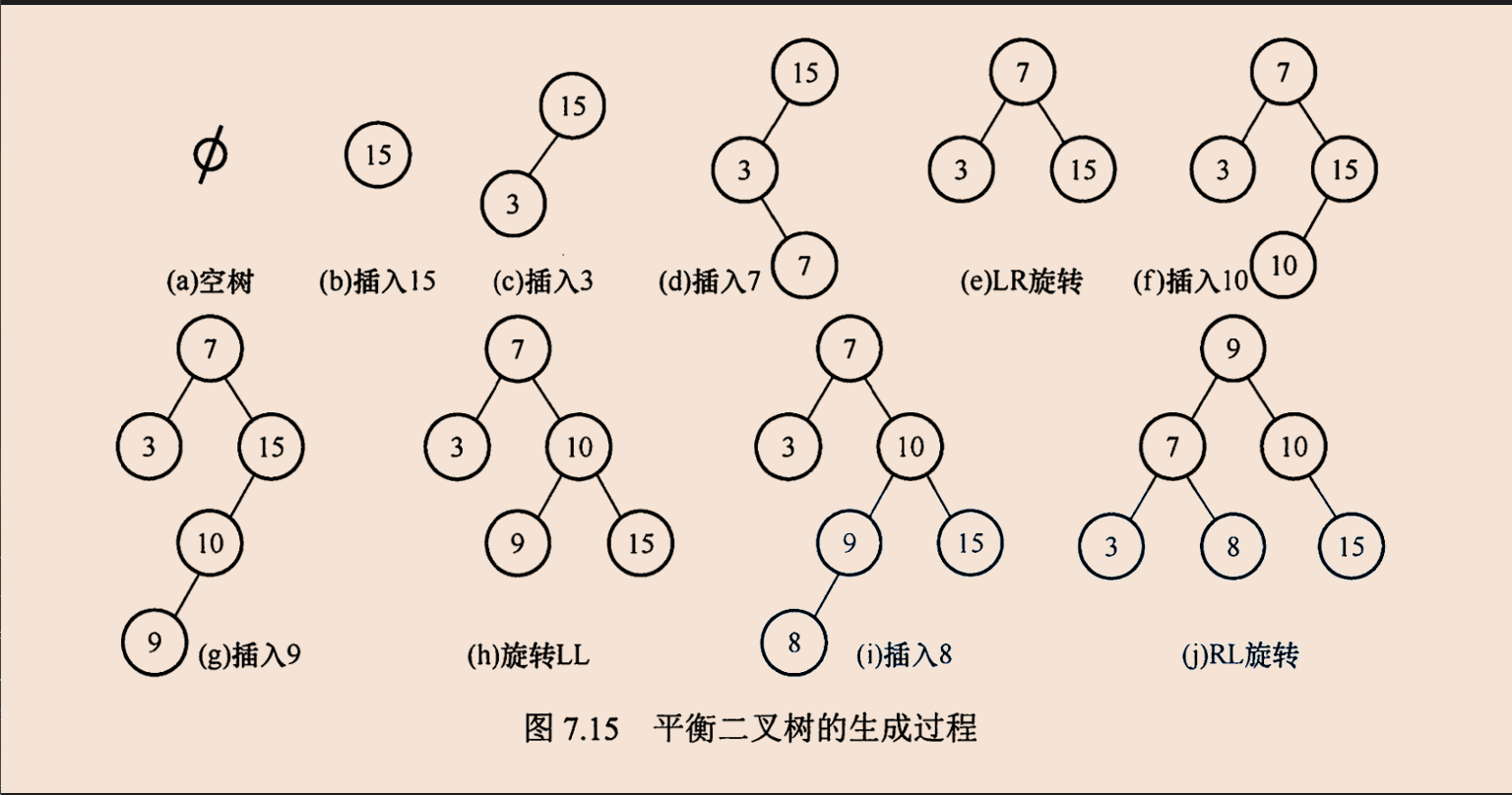
以关键字序列{15,3, 7, 10,9, 8}构造一棵平衡二叉树的过程为例,插入7后导致不平衡,最小不平衡子树的根为15,插入位置为其左孩子的右子树,故执行LR旋转,先左后右双旋转。再插入9后导致不平衡,最小不平衡子树的根为15,插入位置为其左孩子的左子树,故执行LL旋转,右单旋转。再插入8后导致不平衡,最小不平衡子树的根为7,插入位置为其右孩子的左子树,故执行RL旋转,先右后左双旋转,最后结果如图:
代码实现
#include <stdio.h>
#include <stdlib.h>
typedef struct AVLNode {
int key;
int height;
struct AVLNode* left;
struct AVLNode* right;
} AVLNode;
// 获取AVL树高度
int getHeight(AVLNode* node) {
if (node == NULL) {
return 0;
}
return node->height;
}
// 更新结点高度
void updateHeight(AVLNode* node) {
int leftHeight = getHeight(node->left);
int rightHeight = getHeight(node->right);
node->height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
// 获取AVL树平衡因子
int getBalanceFactor(AVLNode* node) {
if (node == NULL) {
return 0;
}
return getHeight(node->left) - getHeight(node->right);
}
// 右单旋转(LL)
AVLNode* rightRotate(AVLNode* A) {
AVLNode* B = A->left;
A->left = B->right;
B->right = A;
updateHeight(A);
updateHeight(B);
return B;
}
// 左单旋转(RR)
AVLNode* leftRotate(AVLNode* A) {
AVLNode* B = A->right;
A->right = B->left;
B->left = A;
updateHeight(A);
updateHeight(B);
return B;
}
// 插入新结点并保持平衡
AVLNode* insertNode(AVLNode* root, int key) {
if (root == NULL) {
AVLNode* newNode = (AVLNode*)malloc(sizeof(AVLNode));
newNode->key = key;
newNode->height = 1;
newNode->left = NULL;
newNode->right = NULL;
return newNode;
}
if (key < root->key) {
root->left = insertNode(root->left, key);
} else if (key > root->key) {
root->right = insertNode(root->right, key);
} else {
return root; // 不允许插入重复值
}
updateHeight(root);
int balanceFactor = getBalanceFactor(root);
// LL旋转
if (balanceFactor > 1 && getBalanceFactor(root->left) > 0) {
return rightRotate(root);
}
// RR旋转
if (balanceFactor < -1 && getBalanceFactor(root->right) < 0) {
return leftRotate(root);
}
// LR旋转
if (balanceFactor > 1 && getBalanceFactor(root->left) < 0) {
root->left = leftRotate(root->left);
return rightRotate(root);
}
// RL旋转
if (balanceFactor < -1 && getBalanceFactor(root->right) > 0) {
root->right = rightRotate(root->right);
return leftRotate(root);
}
return root;
}
// 前序遍历
void preorderTraversal(AVLNode* root) {
if (root == NULL) {
return;
}
printf("%d ", root->key);
preorderTraversal(root->left);
preorderTraversal(root->right);
}
int main() {
AVLNode* root = NULL;
int keys[] = {15, 3, 7, 10, 9, 8};
int n = sizeof(keys) / sizeof(int);
// 插入所有键值
for (int i = 0; i < n; i++) {
root = insertNode(root, keys[i]);
}
// 前序遍历打印
printf("Preorder traversal: ");
preorderTraversal(root);
printf("\n");
return 0;
}
删除操作
与插入操作类似,删除结点时可能导致不平衡,那么我们又需要进行适当的旋转来恢复平衡。
// 删除指定节点中的最小节点并返回更新后的子树。
AVLNode* deleteMinNode(AVLNode *node) {
// 如果节点没有左子树,那么这个节点就是最小节点,用右子树替换它并释放内存。
if (node->left == NULL) {
AVLNode *rightNode = node->right;
free(node);
return rightNode;
}
// 递归地查找并删除左子树中的最小节点。
node->left = deleteMinNode(node->left);
// 对节点进行平衡调整。
return balance(node);
}
// 删除具有指定键值的节点。
AVLNode* removeNode(AVLNode *node, int key) {
// 如果节点为空,直接返回。
if (node == NULL) {
return node;
}
// 如果要删除的键值小于当前节点的键值,则递归地在左子树中删除。
if (key < node->key) {
node->left = removeNode(node->left, key);
}
// 如果要删除的键值大于当前节点的键值,则递归地在右子树中删除。
else if (key > node->key) {
node->right = removeNode(node->right, key);
}
// 如果找到了要删除的节点。
else {
// 情况 1: 节点没有左子树,直接用右子树替换当前节点。
if (node->left == NULL) {
AVLNode *rightNode = node->right;
free(node);
return rightNode;
}
// 情况 2: 节点没有右子树,直接用左子树替换当前节点。
else if (node->right == NULL) {
AVLNode *leftNode = node->left;
free(node);
return leftNode;
}
// 情况 3: 节点同时具有左子树和右子树。
else {
// 找到右子树中的最小节点,并用它的键值替换当前节点的键值。
AVLNode *minNode = findMinNode(node->right);
node->key = minNode->key;
// 删除右子树中的最小节点。
node->right = deleteMinNode(node->right);
}
}
// 对节点进行平衡调整。
return balance(node);
}
// balance operation
AVLNode* balance(AVLNode *node) {
if (node == NULL) {
return node;
}
int balanceFactor = getBalanceFactor(node);
if (balanceFactor > 1) {
if (getBalanceFactor(node->left) >= 0) {
return rightRotate(node); // LL旋转
} else {
node->left = leftRotate(node->left);
return rightRotate(node); // LR旋转
}
} else if (balanceFactor < -1) {
if (getBalanceFactor(node->right) <= 0) {
return leftRotate(node); // RR旋转
} else {
node->right = rightRotate(node->right);
return leftRotate(node); // RL旋转
}
}
return node;
}
在删除节点时,需要根据被删除节点的情况进行不同的操作:
- 如果被删除节点的左子树为空,则将其右子树提升为当前节点的位置。
- 如果被删除节点的右子树为空,则将其左子树提升为当前节点的位置。
- 如果被删除节点的左右子树均不为空,则需要找到其右子树中最小的节点,将其值赋给当前节点,并删除右子树中的最小节点。
查找操作
平衡二叉树的查找操作与二叉排序树的查找操作类似,从根节点开始递归查找:
- 如果当前节点为空,则返回 NULL。
- 如果当前节点的 key 等于查找的值,则返回当前节点。
- 如果当前节点的 key 大于查找的值,则递归查找左子树。
- 如果当前节点的 key 小于查找的值,则递归查找右子树。
AVLNode* search(AVLNode *node, int key) {
if (node == NULL || node->key == key) {
return node;
}
if (key < node->key) {
return search(node->left, key);
} else {
return search(node->right, key);
}
}