《LeetCode》—— 摆动序列

news2024/9/21 18:45:25

今天，我们要讲解的是 “摆动序列” 这道题目。对于这道题目，我们可以从贪心的思想去解决，也可以使用动态规划的方法。接下来，我通过这两种方法的讲解让你轻松拿捏它！

（一）贪心算法

1、上下坡中有平坡

2、数组首尾两端

3、单调坡中有平坡

（二）动态规划

题目链接：摆动序列

题目如下：

（一）贪心算法

题意分析：

摆动序列的意思就是相邻两个元素的差值要保持一正一负这种情况，只有这样数组中的所有元素的分布才是呈现出摆动的情况。

首先，我先把示例 1给大家展开解释一下：

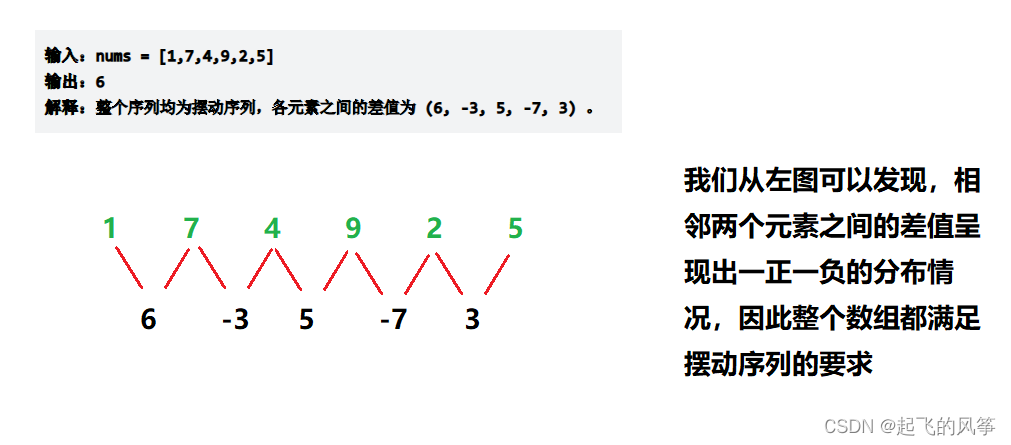
💨 而本题要求是从原始序列中来获得子序列，剩下的元素保持其原始顺序。这就可能会要求删除元素使其达到最大摆动序列的情况，应该“删除”什么元素呢？

1、首先，我们一步步的来考虑，假如题目给出的数组只有两个元素，并且两元素并不相同，那么此时有几个呢？

答案是不是有两个摆动的序列呀！就如下图所表示的那样

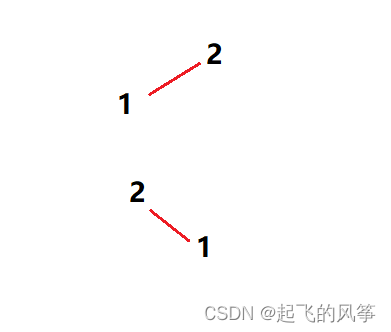
2、其次，对于数组中的元素大于两个的情况，我们有需要额外的去判定，别着急，我们通过题目中给出的例二分析一下在要求“删除”的情况下我们到底需要怎么做：

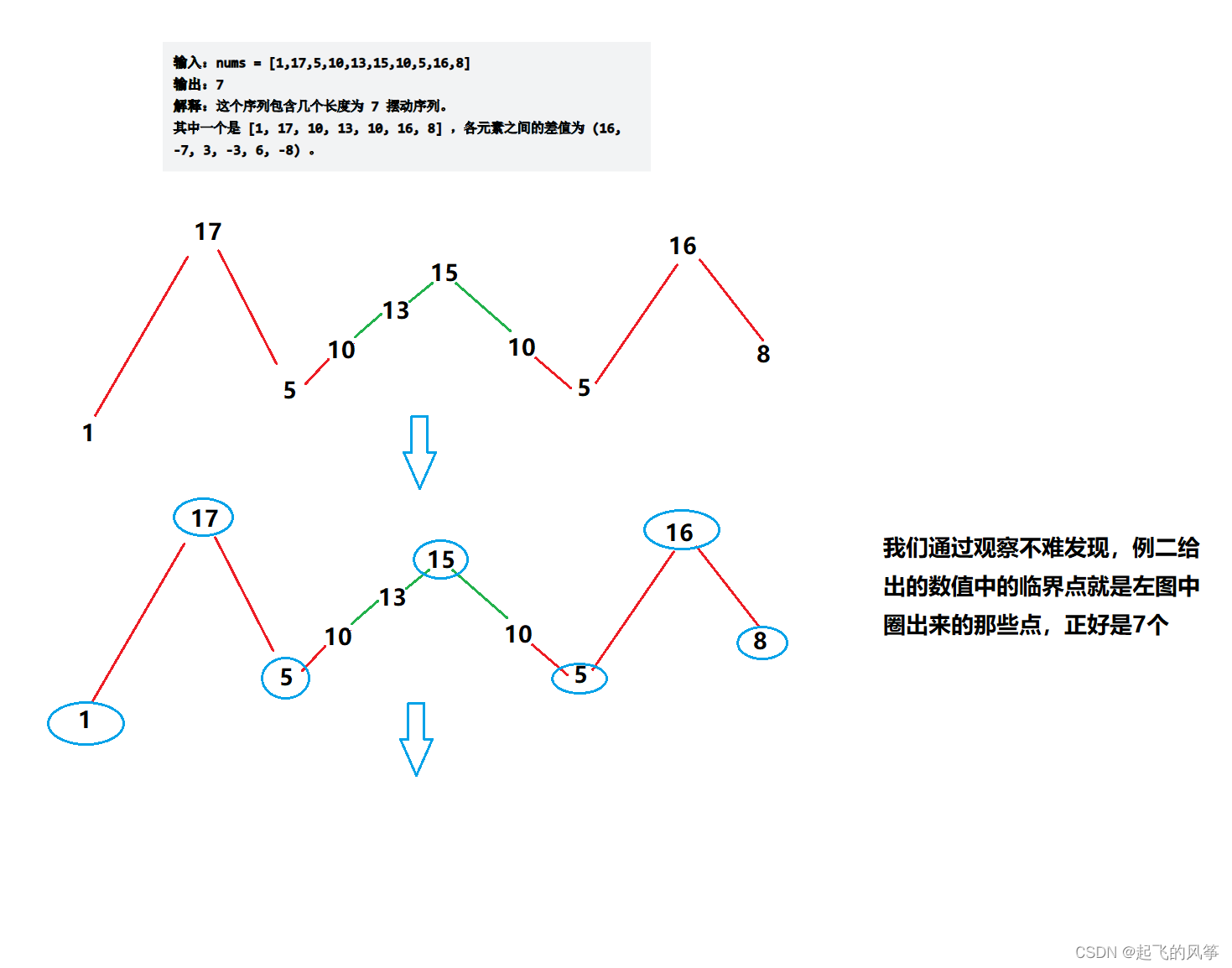
通过上述的观察，我们就可以发现本题的思路其实可以从局部到整体：

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。
整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

因此，我们可以怎么做呢？

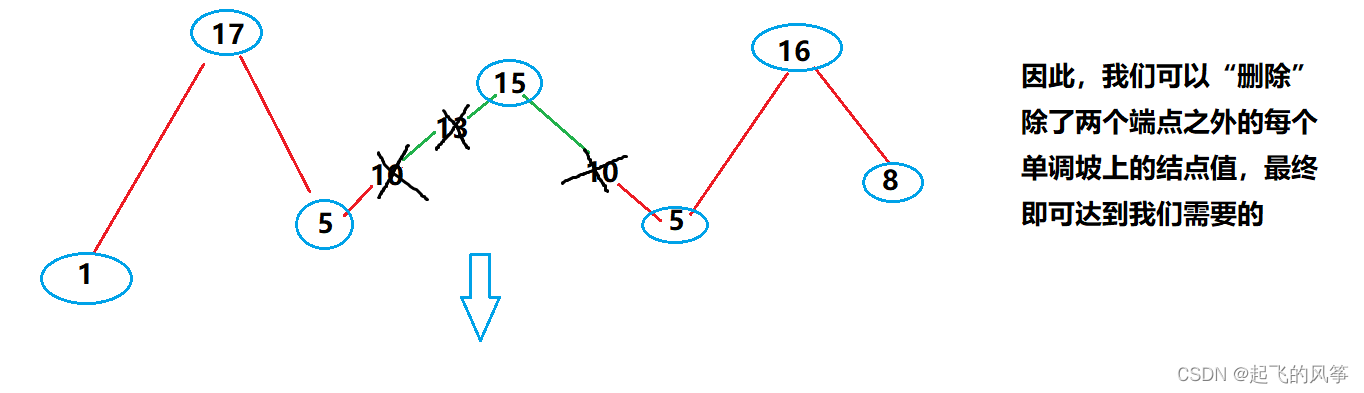
注意：

因此，本道题的整体思路就出来了，当遇到元素摆动的时候，遇到摆动时【Count++】，当遇到单调坡上的元素时，我们就做相应的处理不进行【Count++】操作。
对于我给出的“删除”，并不是真正意义上的删除，我们只需利用条件判断绕开在单调坡上的元素即可。如果大家一股脑的陷入删除去做的话，会显得很复杂的！

接下来，我们就去看看如何判断摆动条件：

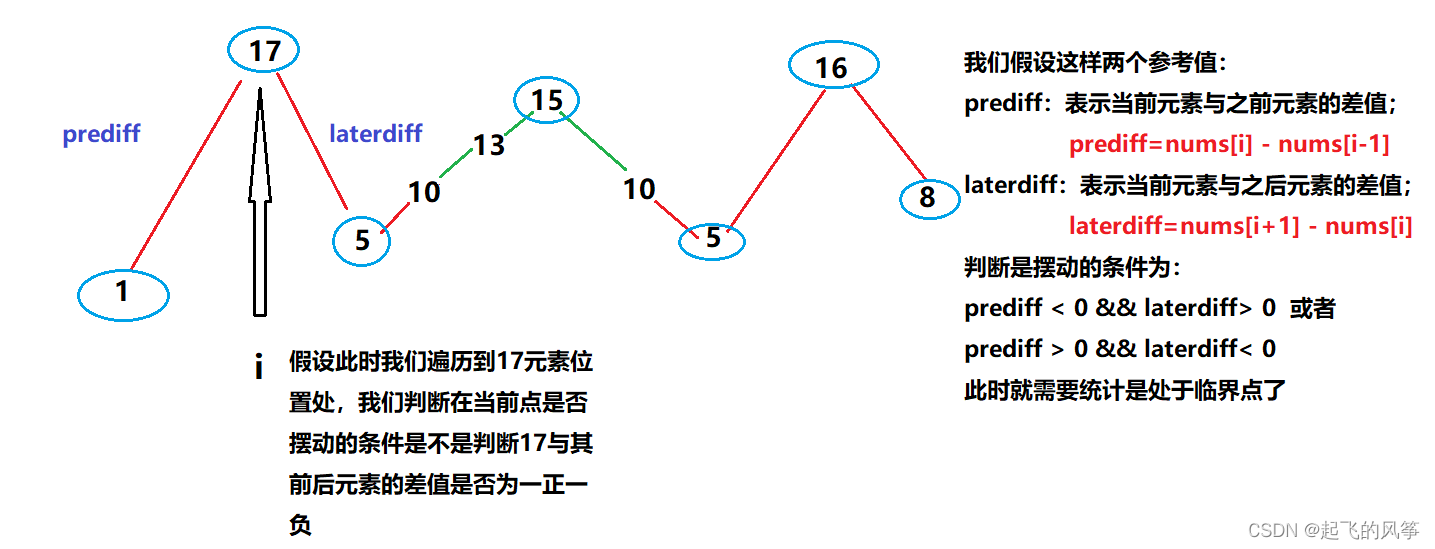
这是我们思考本题的一个大题思路，但本题要考虑三种情况：

上下坡中有平坡
数组首尾两端
单调坡中有平坡

1、上下坡中有平坡

对于上述的例二，相邻元素之间的值是不同的，但是是不是存在这样的一种情况，就是数组中相邻元素之间有相同的情况。

例如 [1,2,2,2,1]这样的数组，如图（把图画出来中间就出现了直平的情况）：

对于上图这种情况它的摆动序列长度是多少呢？其实是长度是3，也就是我们在删除的时候要不删除左面的三个2，要不就删除右边的三个2。

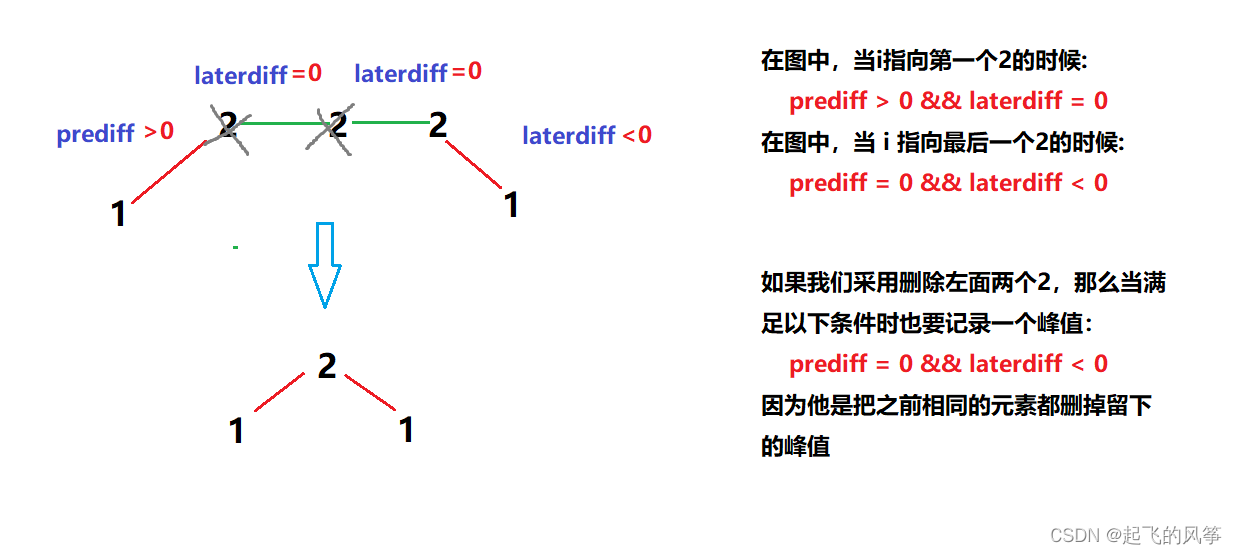
所以，综上所述，我们记录峰值的条件应该是：

(prediff <= 0 && laterdiff > 0) || (prediff >= 0 && laterdiff < 0)

2、数组首尾两端

因为题目给出收尾元素在计算时都是要算坡度的对其，那么我们在处理时也需要对其做相应的处理动作。

在上述的计算方法中，我们通过当前元素，以及当前元素的前一个元素和当前元素的后一个元素去求取两边的差值来判断，但是当题目给出只有两个时，这种方法是不是就满足不了呀！因此，我们还需额外的进行判断这种情况。

对于它的处理办法，有两种：

💨 ①我们可以把条件写死，就是如果只有两个元素，且元素不同，那么结果为2，直接返回即可；

💨 ②为了运用上述的那种规则体系，我们可以在第一个元素之前假入一个元素即可使用上述公式的运行，那这个数字应该是什么呢？

之前我们在讨论情况一时得出过相同数字连续的时候， prediff = 0 ，laterdiff < 0 或者 >0 也记为临界
那么为了规则统一，针对序列[1，2]，可以假设为[1,1,2]，这样它就有坡度了即preDiff = 0，如图：

针对以上情形，res初始为1（默认最右面有一个峰值），此时laterdiff > 0 && prediff <= 0，那么res++（计算了左面的峰值），最后得到的 res=2（峰值个数为2即摆动序列长度为2）

3、单调坡中有平坡

在版本一中，我们忽略了一种情况，即如果在一个单调坡度上有平坡，例如[1,2,2,2,3,4]，如图：

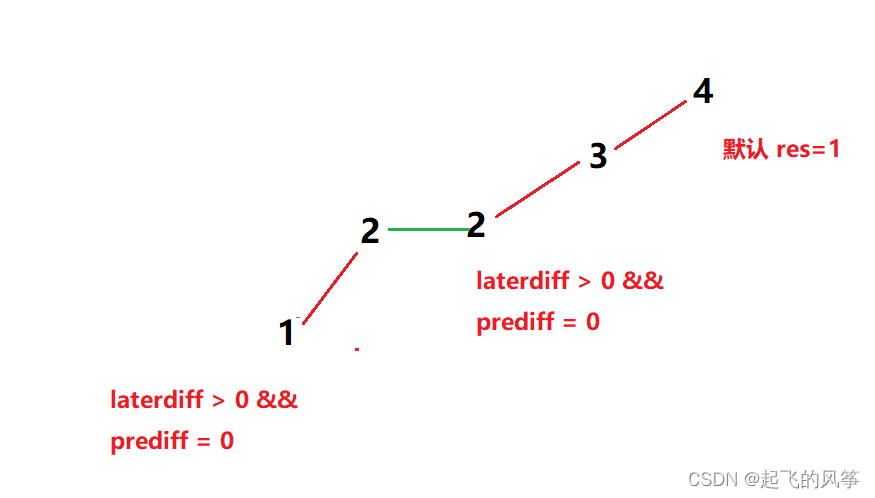
我们先看一下这种情况下摆动的最长序列是多少，通过观察，我们发现本题的最长序列为2，因为单调中的平坡不能算临界。

因此，我们只需要在这个坡度摆动变化的时候，更新prediff就行，这样prediff在单调区间有平坡的时候就不会发生变化，造成我们的误判。

代码展示：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        if (nums.size() <= 1) 
            return nums.size();
            
        int Count = 1;  // 记录峰值个数，序列默认序列最右边有一个峰值
        int prediff = 0; // 当前一对差值
        int laterdiff = 0; // 前一对差值
        

        for (int i = 0; i < nums.size() - 1; i++) {
            prediff = nums[i + 1] - nums[i];
            // 出现峰值
            if ((laterdiff <= 0 && prediff > 0) || (laterdiff >= 0 && prediff < 0)) {
                Count++;
                laterdiff = prediff; // 注意这里，只在摆动变化的时候更新prediff 
            }
        }
        return Count;
    }
};

性能分析：

时间复杂度：O(n)。其中n 是序列的长度。我们只需要遍历该序列一次。
空间复杂度：O(1)。我们只需要常数空间来存放若干变量。

（二）动态规划

根据动态规划的思想，每当我们选择一个元素作为摆动序列的一部分时，这个元素要么是上升的，要么是下降的，这取决于前一个元素的大小。每一个数值处于两种状态，如【1 2 3】，此时2的prediff 处于正值状态，2的 laterdiff 处于负值状态，那么我们需要有两个变量来存储。

由于题目的要求是求出最长的摆动序列，那么动态规划的状态转折表达式中设置两个状态数组：

up[i] ：表示以前 i 个元素中的某一个为结尾的最长的「上升摆动序列」的长度。
down[i] ：表示以前 i 个元素中的某一个为结尾的最长的「下降摆动序列」的长度。

那么流思维导图：

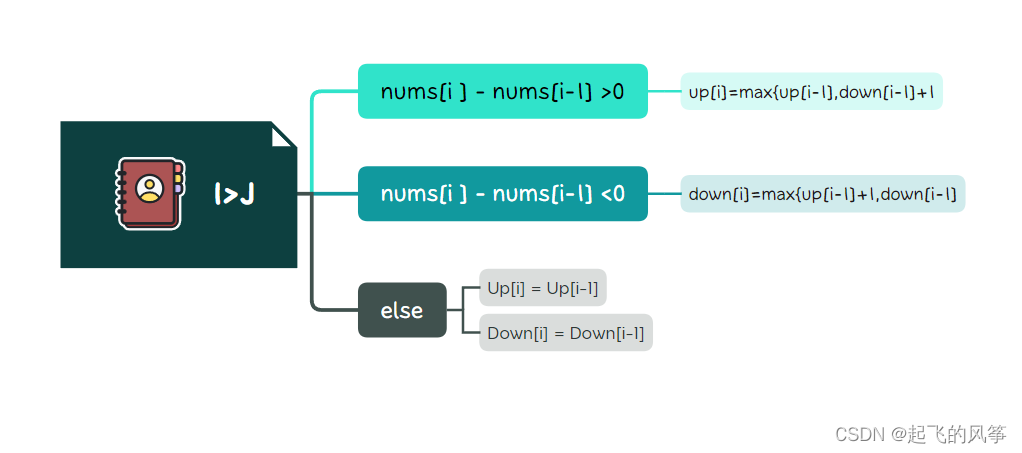
在这一思路上，我们还可以对其进行改进。既然已知每一个数处于的状态，如位置i的数，我们已知位置i前面所有的状态，，那么我们可以一次性遍历即可：：

在上述优化下，我们还可以将空间缩小，因为我们发现每次参加运算的变量只有位置i和位置i - 1两个数，因为，可以直接用两个变量代替即可。

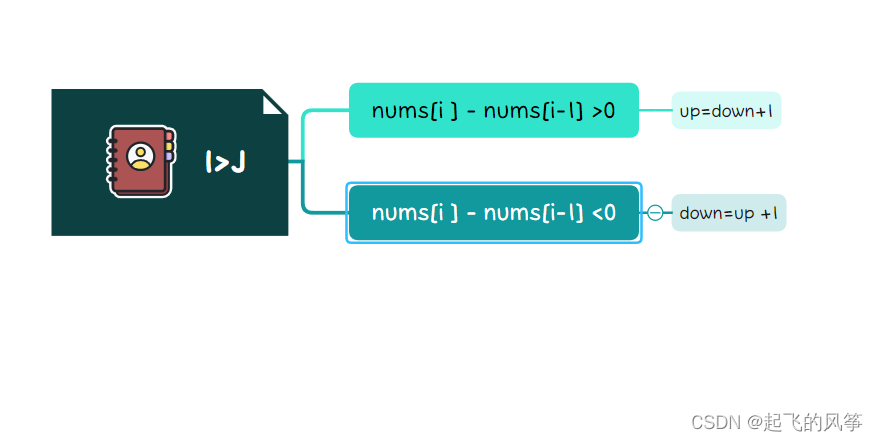
代码展示：

class Solution {
public:
    int wiggleMaxLength(vector<int>& nums) {
        int n = nums.size();
        if(n == 0)
            return 0;
        int up = 1;
        int down = 1;
        for(int i = 1;i < n;++i){
            if(nums[i] - nums[i - 1] > 0)
                up =down + 1;
            else if(nums[i] - nums[i - 1] < 0)
                down =up + 1;
        }
        return max(down,up);
    }
};

性能分析：