1. 实验目的
①掌握逻辑回归的基本原理,实现分类器,完成多分类任务;
②掌握逻辑回归中的平方损失函数、交叉熵损失函数以及平均交叉熵损失函数。
2. 实验内容
①能够使用TensorFlow计算Sigmoid函数、准确率、交叉熵损失函数等,并在此基础上建立逻辑回归模型,完成分类任务;
②能够使用MatPlotlib绘制分类图。
- 实验过程
题目一:
观察6.5.3小节中给出的鸢尾花数据集可视化结果(如图1所示),编写代码实现下述功能:(15分)
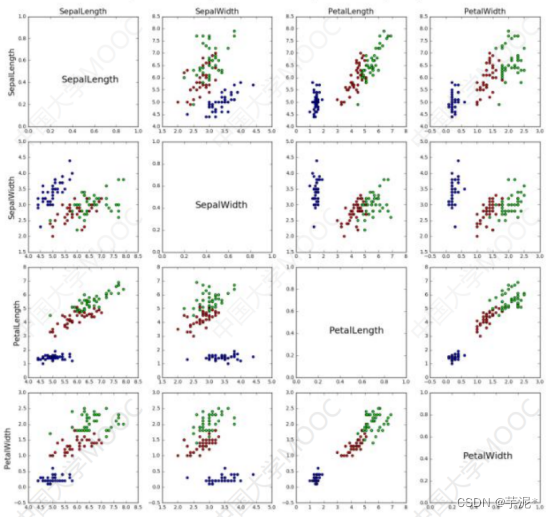
图1 鸢尾花数据集
要求:
⑴选择恰当的属性或属性组合,训练逻辑回归模型,区分山鸢尾和维吉尼亚鸢尾,并测试模型性能,以可视化的形式展现训练和测试的过程及结果。
⑵比较选择不同属性或属性组合时的学习率、迭代次数,以及在训练集和测试集上的交叉熵损失和准确率,以表格或合适的图表形式展示。
⑶分析和总结:
区分山鸢尾和维吉尼亚鸢尾,至少需要几种属性?说明选择某种属性或属性组合的依据;通过以上结果,可以得到什么结论,或对你有什么启发。
① 代码
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
TRAIN_URL='http://download.tensorflow.org/data/iris_training.csv'
train_path=tf.keras.utils.get_file(TRAIN_URL.split('/')[-1],TRAIN_URL)
df_iris=pd.read_csv(train_path,header=0)
iris=np.array(df_iris)#把二维数据表转化成二维numpy数组
train_x=iris[:,0:2]#取花萼的长度和宽度
train_y=iris[:,4]#取最后一列作为标签值
x_train=train_x[train_y!=1] #提取山鸢尾与维吉尼亚鸢尾
y_train=train_y[train_y!=1]
#使用花萼长度和花萼宽度作为样本画散点图
num=len(x_train)
cm_pt=mpl.colors.ListedColormap(['b','r'])
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt) #色彩方案
# plt.show()
#使用花萼长度和花萼宽度作为样本画散点图 中心化后的图
x_train=x_train-np.mean(x_train,axis=0) #属性中心化 按列
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
# plt.show()
#生成多元模型的属性矩阵和标签列向量X,Y
x0_train=np.ones(num).reshape(-1,1)
X=tf.cast(tf.concat((x0_train,x_train),axis=1),tf.float32)
Y=tf.cast(y_train.reshape(-1,1),tf.float32)
#设置超参数
learn_rate=0.03
iter=50
display_step=10
#设置模型变量初始值
np.random.seed(612)
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)
#训练模型
ce=[]#保存每次交叉熵损失
acc=[]#保存准确率
for i in range(0,iter+1):
with tf.GradientTape() as tape:
PRED=1/(1+tf.exp(-tf.matmul(X,W)))
Loss=-tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))
accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
ce.append(Loss)
acc.append(accuracy)#加入数据
dL_dW=tape.gradient(Loss,W)
W.assign_sub(learn_rate*dL_dW)
if i % display_step ==0:
print('i:%i,Acc:%f,Loss:%f'%(i,accuracy,Loss))
#可视化
plt.figure(figsize=(5,3))
plt.plot(ce,color='b',label='Loss')
plt.plot(acc,color='r',label='acc')
plt.legend()
# plt.show()
#绘制决策边界
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
x_=[-1.5,1.5]
y_=-(W[1]*x_+W[0]/W[2])
plt.plot(x_,y_,color='g')
# plt.show()
np.random.seed(612)
W=tf.Variable(np.random.randn(3,1),dtype=tf.float32)
cm_pt=mpl.colors.ListedColormap(['b','r'])
x_=[-1.5,1.5]
y_=-(W[0]+W[1]*x_)/W[2]
#绘制训练集的散点图
plt.scatter(x_train[:,0],x_train[:,1],c=y_train,cmap=cm_pt)
plt.plot(x_,y_,color='r',lw=3)
plt.xlim([-1.5,1.5])
plt.ylim([-1.5,1.5])
#在训练过程中显示训练结果
ce=[]
acc=[]
for i in range(0,iter+1):
with tf.GradientTape() as tape:
PRED=1/(1+tf.exp(-tf.matmul(X,W)))
Loss=-tf.reduce_mean(Y*tf.math.log(PRED)+(1-Y)*tf.math.log(1-PRED))
accuracy=tf.reduce_mean(tf.cast(tf.equal(tf.where(PRED.numpy()<0.5,0.,1.),Y),tf.float32))
ce.append(Loss)
acc.append(accuracy)
dL_dW=tape.gradient(Loss,W)
W.assign_sub(learn_rate*dL_dW)
if i % display_step ==0:
print('i:%i,Acc:%f,Loss:%f'%(i,accuracy,Loss))
y_=-(W[0]+W[1]*x_)/W[2]
plt.plot(x_,y_)
plt.show()② 结果记录
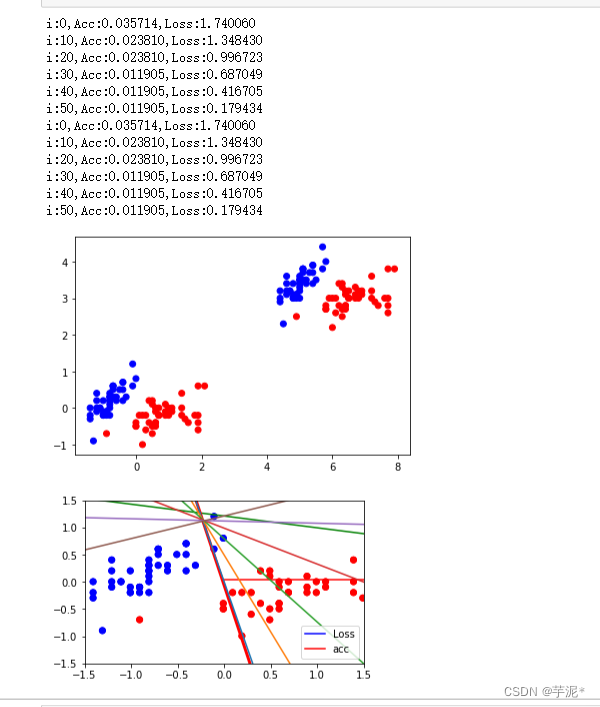
③ 实验总结
在训练集上训练的模型在测试集上也有比较好的效果,超参数需要不断调试才能达到一个比较好的效果.
题目二:
在Iris数据集中,分别选择2种、3种和4种属性,编写程序,区分三种鸢尾花。记录和分析实验结果,并给出总结。(20分)
⑴确定属性选择方案。
⑵编写代码建立、训练并测试模型。
⑶参考11.6小节例程,对分类结果进行可视化。
⑷分析结果:
比较选择不同属性组合时的学习率、迭代次数、以及在训练集和测试集上的交叉熵损失和准确率,以表格或合适的图表形式展示。
(3)总结:
通过以上分析和实验结果,对你有什么启发。
① 代码
import tensorflow as tf
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Droid Sans Fallback']
# 下载鸢尾花数据集
TRAIN_URL = 'http://download.tensorflow.org/data/iris_training.csv'
TEST_URL = 'http://download.tensorflow.org/data/iris_test.csv'
# 获取文件名
train_path = tf.keras.utils.get_file(TRAIN_URL.split('/')[-1], TRAIN_URL)
test_path = tf.keras.utils.get_file(TEST_URL.split('/')[-1], TEST_URL)
COLUMN_NAMES = ['SepalLength', 'SepalWidth', 'PetalLength', 'PetalWidth', 'Species']
df_iris_train = pd.read_csv(train_path, header=0)
iris_train = np.array(df_iris_train)
# 提取长度,宽度
# x_train = iris_train[:, 2:4]
# y_train = iris_train[:, 4]
#花萼宽度、花瓣长度、花瓣宽度
x_train = iris_train[:, 1:3]
y_train = iris_train[:, 4]
x_train=x_train[y_train>0]
y_train=y_train[y_train>0]
num_train = len(x_train)
#处理数据
x0_train = np.ones(num_train).reshape(-1, 1)
X_train = tf.cast(tf.concat([x0_train, x_train], axis=1), tf.float32)
Y_train = tf.one_hot(tf.constant(y_train, dtype=tf.int32), 3)
#设置超参数 设置模型参数初始值
learn_rate = 0.2
iter = 500
display_step = 50
np.random.seed(612)
W = tf.Variable(np.random.randn(3,3), dtype=tf.float32)
#训练模型
acc = []
cce = []
for i in range(0, iter + 1):
with tf.GradientTape() as tape:
PRED_train = tf.nn.softmax(tf.matmul(X_train, W))
Loss_train = -tf.reduce_sum(Y_train * tf.math.log(PRED_train)) / num_train
accuracy = tf.reduce_mean(tf.cast(tf.equal(tf.argmax(PRED_train.numpy(), axis=1), y_train), tf.float32))
acc.append(accuracy)
cce.append(Loss_train)
dL_dW = tape.gradient(Loss_train, W)
W.assign_sub(learn_rate * dL_dW)
if i % display_step == 0:
print('i:%i,Acc: %f,Loss: %f' % (i, accuracy, Loss_train))
#绘制分类图
M = 500
x1_min, x2_min = x_train.min(axis=0)
x1_max, x2_max = x_train.max(axis=0)
t1 = np.linspace(x1_min, x1_max, M)
t2 = np.linspace(x2_min, x2_max, M)
m1, m2 = np.meshgrid(t1, t2)
m0 = np.ones(M * M)
X_ = tf.cast(np.stack((m0, m1.reshape(-1), m2.reshape(-1)), axis=1), tf.float32)
Y_ = tf.nn.softmax(tf.matmul(X_, W))
Y_ = tf.argmax(Y_.numpy(), axis=1) #转化为自然顺序码,决定网格颜色
n = tf.reshape(Y_, m1.shape)
#绘制分类图
plt.figure(figsize=(8, 6))
cm_bg = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
plt.pcolormesh(m1, m2, n, cmap=cm_bg)
plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train, cmap='brg')
plt.show()② 结果记录
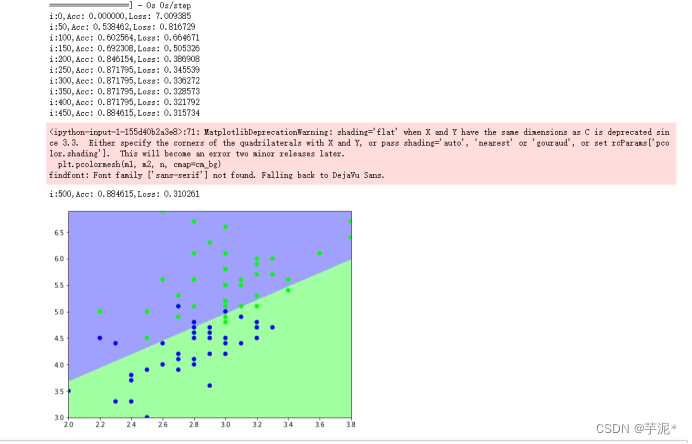
③ 实验总结
在训练集上训练的模型在测试集上也有比较好的效果,超参数需要不断调试才能达到一个比较好的效果.
| 学习率 | 训练轮数 | 测试损失值 | 测试集准确率 | 所花时间 | |
| 1 | 1e-3 | 1000 | 0.483739 | 87.2% | 1.73s |
| 2 | 1e-4 | 10000 | 0.483747 | 87.2% | 16.68s |
| 3 | 5e-2 | 1000 | 0.211227 | 93.6% | 1.73s |
拓展题(选做):
乳腺癌肿瘤数据集,由威斯康辛大学麦迪逊医院的William博士提供,可在UCI数据库(加州大学欧文分校提出的用于机器学习的数据库)里下载。
下载地址:https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data
该数据集中有699个乳腺癌肿瘤样本,每个样本包含10个属性和1个肿瘤标签,其结构如图1所示。第1列为id号,第2-10列为肿瘤特征,第11列为肿瘤的标签。每个属性的属性值均为0-9之间的整数,标签值取2或4,2表示良性、4表示恶性。
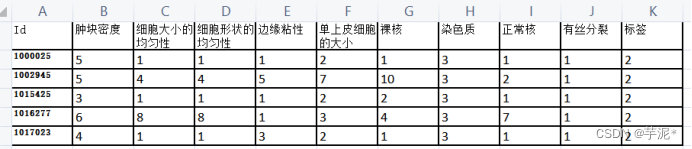
图1 乳腺癌肿瘤数据集(前5行数据)
要求:
⑴下载并划分数据集:
下载数据集,合理划分为训练集和测试集;
⑵数据预处理:
数据集中有16处缺失值,用“?”表示,在将数据输入模型之前,需要对这些缺失值进行处理。首先将“?”替换为NaN,再丢弃缺失值所在的样本,最后对已经丢弃缺失值的数组索引进行重置;
相关函数:
| 序号 | 函数 | 函数功能 | 函数相关库 |
| (1) | 对象名.replace(to_replace=’?’,value=np.nan) | 将问号替换为NaN | Python内置函数 |
| (2) | 对象名.dropna() | 丢弃缺失值 | Pandas库 |
| (3) | 对象名.reset_index() | 索引重置 | Pandas库 |
(3)建立逻辑回归模型,使用属性“肿块密度”和“细胞大小的均匀性”训练模型,综合考虑准确率、交叉熵损失、和训练时间等,使模型在测试集达到最优的性能,并以合适的形式展现训练过程和结果;
(4)选择其他属性或属性组合训练模型:
尝试选择数据集中的其他属性或者属性组合,训练和测试逻辑回归模型,并展现训练过程和结果;
(5)分析和总结:
比较采用不同的属性或属性组合训练模型时,学习率、迭代次数,以及交叉熵损失、准确率和模型训练时间等,以表格或其他合适的图表形式展示。通过以上结果,可以得到什么结论,或对你有什么启发。
① 代码
② 结果记录
③ 实验总结
3. 实验小结&讨论题
①实现分类问题的一般步骤是什么?实现二分类和多分类问题时有什么不同之处?哪些因素会对分类结果产生影响?
答:1.问题的提出2.神经网络模型的搭建和训3.结果展示。
多分类:
每个样本只能有一个标签,比如ImageNet图像分类任务,或者MNIST手写数字识别数据集,每张图片只能有一个固定的标签。
对单个样本,假设真实分布为,网络输出分布为,总的类别数为,则在这种情况下,交叉熵损失函数的计算方法如下所示,我们可以看出,实际上也就是计算了标签类别为1的交叉熵的值,使得对应的信息量越来越小,相应的概率也就越来越大了。
二分类:
对于二分类,既可以选择多分类的方式,也可以选择多标签分类的方式进行计算,结果差别也不会太大
②将数据集划分为训练集和测试集时,应该注意哪些问题?改变训练集和测试集所占比例,对分类结果会有什么影响?
答:同样的迭代次数,和学习率下,随着训练集的比例逐渐变大,训练集交叉熵损失大致变小准确率变高的趋势,测试集交叉熵损失大致变大准确率变高的趋势。
③当数据集中存在缺失值时,有哪些处理的方法?查阅资料并结合自己的思考,说明不同处理方法的特点和对分类结果的影响。
答:(1)删除,直接去除含有缺失值的记录,适用于数据量较大(记录较多)且缺失比较较小的情形,去掉后对总体影响不大。
(2)常量填充,变量的含义、获取方式、计算逻辑,以便知道该变量为什么会出现缺失值、缺失值代表什么含义。
(3)插值填充,采用某种插入模式进行填充,比如取缺失值前后值的均值进行填充。
(4)KNN填充
(5)随机森林填充,随机森林算法填充的思想和knn填充是类似的,即利用已有数据拟合模型,对缺失变量进行预测。