2.4.1多项式的加法运算实现

注：这里的多项式只局限于一元多项式

如何设计一个函数分别求两个一元多项式的和？

观察多项式求和的过程规律，对于次数不同的项我们直接放到最终结果中即可，对于次数相同的项才进行加减运算。于是我们可以用一个不带头结点的单向链表，按照指数递减的顺序来排列每一项，来实现多项式加法。

算法思路：两个指针p1，p2分别指向两个多项式的第一个结点（最高项）并循环

循环：

p1指数=p2指数：二者系数做相加，若结果不为0则添加到结果多项式中，p1和p2都向后挪一项
p1指数>p2指数：p1当前项添加到结果多项式，p1指向下一项
p1指数<p2指数：p2当前项添加到结果多项式，p2指向下一项

当其中一个多项式已经处理完毕，就将另一个多项式的所有节点全部添加到结果多项式中。

struct PolyNode{
    int coef;//系数
    int expon;//指数
    struct PolyNode *link;//指向下一个结点的指针
};
typedef struct PolyNode *Polynomial;
Polynomial p1,p2;

//c代表系数，e代表指数，pRear代表此时最后一个结点的指针位置（二级指针）
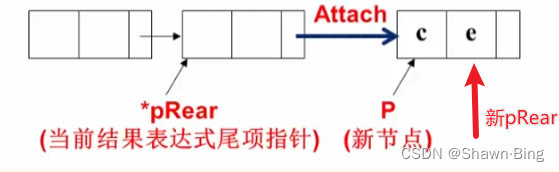
void Attach(int c,int e,Polynomial *pRear)
{
    Polynomial P;
    
    P = (Polynomial)malloc(sizeof(struct PolyNode));
    
    //新结点赋值
    P->coef = c;
    P->expon = e;
    P->link = NULL;
    
    //将P插入到pRear之后
    (*pRear)->link = P;
    *pRear = P;
}

加法的大体框架：三个循环，一个比较t1和t2，两个分别测试多项式是否为空。

Polynomial PolyAdd(Polynomial p1,Polynomial p2)
{
    int sum;
    
    //定义结果多项式的头、尾、临时头结点
    Polynomial front,rear,temp;
    rear = (Polynomial)malloc(sizeof(struct PolyNode));
    front = rear;

    while(p1&p2){
        switch(Compare(p1->expon,p2->expon)){
            case 1://说明p1指数更高
                
                //添加结果，把现在的系数和指数接到结果多项式尾后
                Attach(p1->coef,p1->expon,&rear);

                p1 = p1->link;//后移
                break;
            case -1://p2指数更高
                Attach(p2->coef,p2->expon,&rear);//添加结果
                p2 = p2->link;//后移
                break;
            case 0:
                sum = p1->coef + p2->coef;
                if(sum){//如果系数和不为0的话，sum为计算后系数
                    Attach(sum,p1->expon,&rear);
                }
                p1 = p1->link;
                p2 = p2->link;
                break;
        }
    }

    //把没处理完的另一个多项式的所有节点遍历复制到结果多项式里
    
    //处理p1(p1不空)
    for(;p1;p1 = p1->link){
        Attach(p1->coef,p1->expon,&rear);
    }
    for(;p2;p2 = p2->link){
        Attach(p2->coef,p2->expon,&rear);
    }
    
    //rear指向结果多项式最后一项，由于全部处理完毕，用不到了
    rear->link = NULL;
    
    //为了释放temp，将其赋给fornt，fornt向后挪
    temp = front;
    front = front->link;//fornt指向结果多项式第一个非0项
    free(temp);//释放临时头结点
    return front;
}

2.4.2 多项式的乘积

多项式的乘积，需要用一个多项式的每一项和另一个多项式的每一项相乘，具体来说需要每项系数相乘、指数相加，然后将乘积加在一起得出结果。与加法类似的，指数相同的项，其系数需要合并。

若以以下格式规定输入和输出样例：

项数第一项系数第一项指数第二项系数 ...

并在输出中分别列出

多项式相乘的结果
多项式相加的结果

这个问题可以细分为若干个小问题：

如何表示多项式
如何搭建程序框架
如何读入多项式
加法实现
乘法实现
多项式输出

1.多项式的表示

最佳策略：仅表示非零项

用于实现的数据类型：

	数组	链表
优点	代码简单，调试容易	动态性强
缺点	需要事先确定数组大小（可用动态数组解决）	代码复杂，调试困难

2.程序框架搭建

3.如何读入多项式

4.加法实现

加法的具体实现前文已经提过

5.乘法实现

方法1：把乘法运算转换为加法运算。

先把p1第一项乘以p2每一项，再把第二项乘以p2每一项...最后相加到结果多项式里

方法2：逐项插入。（本次程序使用）

也就是把p1第一项乘以p2第一项，插入到结果多项式。再用p1第一项乘以p2第二项，插入结果多项式...此算法关键是寻找插入位置。结果多项式的初步形式可以用p1第一项乘以p2每一项。

6.多项式输出

以下还是用链表来实现（为了易读而分开了）

//设计多项式数据结构
typedef struct PolyNode *Polynomial;
struct PolyNode{
    int coef;
    int expon;
    Polynomial link;
};

//插入项
void Attach(int c,int e,Polynomial *pRear){
    Polynomial p;
    p = (Polynomial)malloc(sizeof(struct PolyNode));
    p->coef = c;
    p->expon = e;
    p->link = NULL;
    (*pRear)->link = p;
    *pRear = p;
    //让rear结点一开始指向链表头，这样之后插入的多项式都在其之后
}

//读入多项式
PolyNomial ReadPoly(){
    PolyNomial p,Rear,temp;
    int c,e,N;

    scanf("%d",&N);
    //创建链表头空结点
    p = (PolyNomial)malloc(sizeof(struct PolyNode));
    p->link = NULL;
    Rear = p;

    while(N--){
        scanf("%d %d",&c,&e);
        Attach(c,e,&Rear);
    }
    
    t = p; p = p->link; free(t);//删除临时头结点

    return p;
}

//相乘
Polynomial Mult(Polynomial p1,Polynomial p2){
    Polynomial p, Rear, t1, t2, t;
    int c,e;

    //判断p1p2是否为空
    if(!p1 || p2)
        {return NULL;}

    //为了循环计算，需要创建临时变量
    t1 = p1;t2 = p2;
    p = (Polynomial)malloc(sizeof(struct PolyNode));
    p->link = NULL;
    Rear = p;

    //p1第一项乘以p2每一项
    while(t2){
        Attach(t1->coef * t2->coef, t1->expon + t2->expon, &Rear);
        t2 = t2->link;//向后挪一项
    }
    t1 = t1->link;
    while(t1){
        t2 = p2;
        Rear = p;

        while(t2){
            e = t1->expon + t2->expon;
            c = t1->coef * t2->coef;

            //已有有序序列，将新值按序插入
            //比较Rear指向的下一个结点指数与当前要插入结点的指数
            while((Rear->link && Rear->link->expon) > e)
            {Rear = Rear->link;}

            //若Rear下一项指数=要插入项指数
            if((Rear->link && Rear->link->expon) == e){
                if(Rear->link->coef + c)
                    //则不需要申请结点，让系数相加就行
                    {Rear->link->coef += c;}
                

                //如相加后=0就删掉
                else{
                    t = Rear->link;
                    Rear->link = t->link;
                    free(t);
                }
            }else{//需要申请新结点
                t = (Polynomial)malloc(sizeof(struct PolyNode));
                t->coef = c;t->expon = e;
                t->link = Rear->link;
                Rear->link = t;Rear = Rear->link;
                t2 = t2->link;
            }
            t1 = t1->link;
        }//while(t1)结束
        t2 = p; p = p->link;free(t2);//删除空结点

        return p;
    }
}

//输出多项式
void PrintPoly(Polynomial p){
    int flag = 0;//调整输出格式的变量

    if(!p){
        printf("0 0\n");
        return;
    }
    
    while(p){
        if(!flag)//第一项，flag为0不输出
            flag = 1;
        else//非第一项，flag为1输出一个空格
            printf(" ");
        printf("%d %d",p->coef,p->expon);
        p = p->link;
    }
    printf("\n");
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/511165.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！