1.贝叶斯与全概率公式解释
1.全概率公式定义

即若在某个场景下,可找到一个完备事件组 Ai ( i = 1,2,3…n)。
则对任一与该场景有关的事件 B,都可以分割成无数个小事件(由不同因素引起的事件) 有:
B = B ∩ A1 ∪ A2 ∪ A3 ∪ … ∪ An
且
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3) + … +P(An)P(B/An)
注:
1.“与该场景有关的事件 B”:
全概率公式是用于计算某个“结果”(事件)B发生的可能性大小。
如果某个“结果” B (事件) 的发生总是与某些前提条件(原因,因素或前一阶段的结果)Ai(完备事件组)相关联,那么在计算 P(B) 时,我们可以用 Ai 对 B 进行分解:
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2) + P(A3)P(B/A3) + … +P(An)P(B/An)。
因此,我们也叫全概率公式为全集分解法。
2.“P(B) 与 P(B|A)的区别”
二者都是计算 事件B 的概率的,但是前者 P(B) 是在样本空间 Ω 下计算的,后者 P(B|A)是在 事件A 已经发生的条件下计算的(样本空间缩小至A)。
2.贝叶斯公式定义
如果某个场景可以找到一个完备事件组 Ai。则对于 任意与该场景有关的事件 B 有:
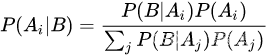
3.全概率公式的推导

2.什么时候用全概率公式和贝叶斯公式
1.全概率公式
1.在某个场景找到一个完备事件组
2.不知道 事件B 的结果,只知道若干个因(完备事件组 Ai)
即在某场景下,某个 事件B 发生是在 "多个因素或条件"下发生的,这些因素构成完备事件组 Ai .
事件B也因此由不同完备事件组成员,分割成无数个小事件.即:
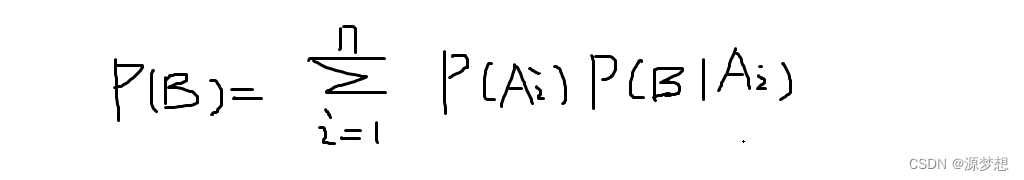
2.贝叶斯公式
贝叶斯公式分母用到了全概率的结果,因此:
1.在个场景找到一个完备事件组
2.知道某个 事件B 已经发生了,结果确定了(这个事件的概论可以用全概率公式求出),然后反过来求组成 事件B 的完备事件组中某个因素的概论。即:
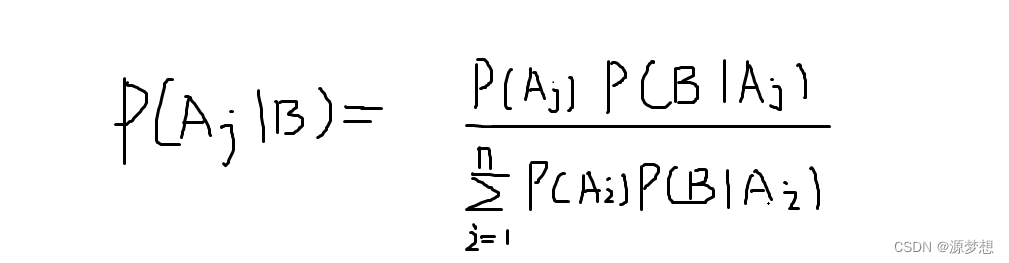
3.全概率公式和贝叶斯公式区别于联系
1.先验概率:

即,先验概率是我们在未知条件下对事件发生可能性猜测。
2.后验概率:

即,后验概率是指在得到“结果”的信息后重新修正的概率,是“执果寻因”问题中的“因” 事情已经发生,要求这件事情发生的原因是由某个因素引起的可能性的大小。
3.联系
①全概率公式描述了一种基于先验概率和条件概率推导出后验概率的方法,它是由贝叶斯公式演化而来的。全概率公式通过将所有可能的事件划分为,互后且完备的事件集合,并计算它们的概率从而推导出后验概率。
②贝叶斯公式是用于计算“逆概率”的公式,即已知某种结果出现的概率,求当前这种结果的特定概率。它同样也是通过先验概率和条件概率计算出后验概率的方法。
4.区别
①两者处理的对象不同,全概率公式用来计算复杂事件的概率,而贝叶斯公式是用来计算简单条件下发生的复杂事件。也就是是说,全概率公式是计算普通概率的,贝叶斯公式是用来计算条件概率的。
②总的来说,全概率公式是用来求解不同情况下的条件概率的,而贝叶斯公式是用来根据观察到的事件推测其原因的概论。两者都是基于先验概率和条件概率计算出后验概率的方法。
4.为什么贝叶斯公式修正了某事件发生因素的概率?
贝叶斯定理意义就是在于 “修正” 二字!
①在使用全概率公式求出某个已知事件之前,我们是没有任何信息的,于是我们无奈根据情况假设概率:
如:每箱产品有10件,可能有 0 1 2件次品,任意抽取1次…题目叙述至此。
我们不知道任何信息,如不知道 抽到正品这件事概率为x等。我们只好假设,每箱为 0 1 2件次品的概率相同(看题目给的概率),即,完备事件组成员概率都为 1/3.
②当我们用全概率公式求出某个事件概率(假设事件B 用完备事件组将B事件分割累加求出),如任取1件为次品这件事概率为x。
于是接下来,我们用贝叶斯公式,是基于事件B 已知 。反过来求,某个完备组成员基于事件B的概率。
综上:
①一个是不知任何信息,迫于无奈合理假设的概率。
②一个是,基于已知事件反过来修正某个因素(某个完备事件组成员)发生的概率。
由于增加了已知事件,而导致某个参与构建该事件的因素的概率发生修正,已知事件越多,概率越精确,这或许就是贝叶斯的意义把。
5.经典例题1–全概率公式
明天写