分子动力学基础知识
目前主要存在两种基本模型:其一为量子统计力学, 其二为经典统计力学。
量子统计力学
- 基于量子力学原理, 适用 于微观的, 小尺度, 短时 间的模拟,可以描述电子 的结构分布,原子间的成 键断键等化学性质。
经典纭计力学
- 基于牛顿经典力学, 模拟 的尺度和时间相比于量子 统计力学较大, 它以每个 原子作为一个质点, 主要 研究课题的物理性质。
分子动力学历史
分子力学思想的萌芽-D. H. Andrews(1930年工作)
在分子内部, 化学键都有 “自然” 的键长值和 键角值。整个分子有如下构象转变趋势:分子的键 长和键角趋于 “自然”状态, 同时, 非键作用(van der Waals) 力也趋于最低状态。以达到原子核排布 的最佳位置。在某些有张力的分子体系中分子的张 力可以计算出来。
分子经典力学模型一T. L. Hill(1946年工作)
T.L.Hill提出用van der Waals相互作用 和键长、键角的形变势能来计算分子的能 量, 用以优化分子空间构型的标准和路径 方向。
该理论认为分子内部的空间作用服从 以下规律:1)基团或原子之间靠近时则两 者之间排斥作用增强;2)为了减少这种排 斥作用,基团或原子间就有相互远离的趋 势, 但是这种运动又会导致键长伸长或键 角发生弯曲, 从而导致相应的能量升高。
分子力学基本假设
在玻恩 - 奥本海默近似下, 体系波函数可以被 写为电子波函数与原子核波函数的乘积:
Ψ
total
=
χ
electronic
×
ϕ
nuclear
\Psi_{\text {total }}=\chi_{\text {electronic }} \times \phi_{\text {nuclear }}
Ψtotal =χelectronic ×ϕnuclear
假设一: 原子的自身运动服从Born-Oppenheimer Approximation, 又称绝热近似 或定核近似:电子与核的质量相差极大, 当核的分布发生微小变化时, 电子能够迅速调整其运动状态以适应新的核势场,而核对电子在其轨道 上的迅速变化却不敏感。通俗讲:原子核的运动与电子的运动可以看成是相互独立的。
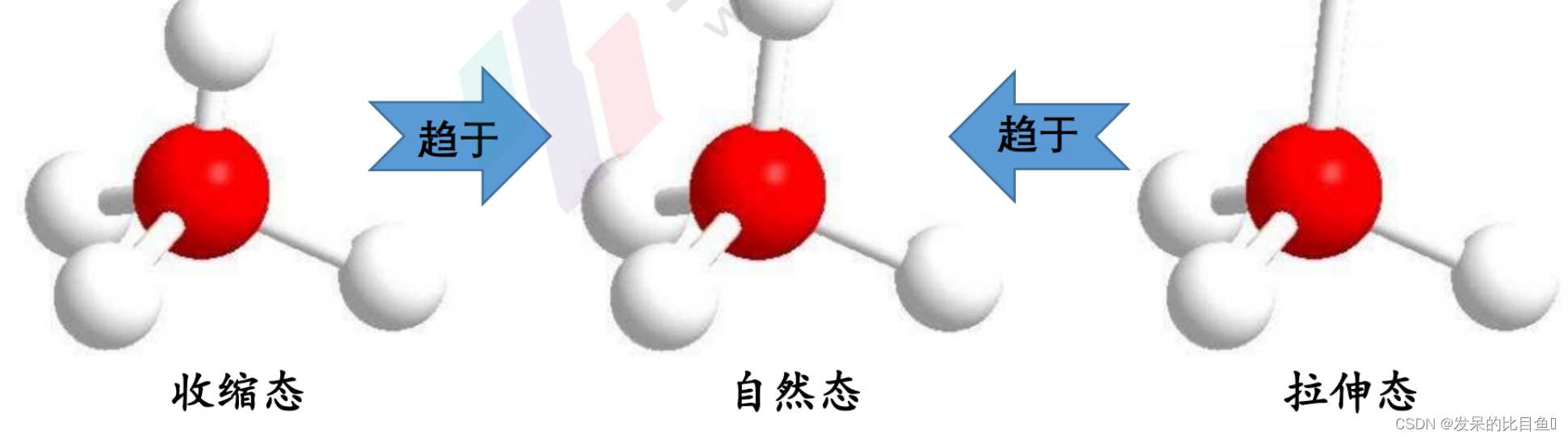
假设二: 分子是一组靠各种作用力维系在一起的原子集合。这些原子在空间上若 过于靠近, 便相互排斥; 但又不能远离, 否则连接它们的化学键以及由 这些键构成的键角等会发生变化,即出现键的拉伸或压缩、键角的扭变 等, 会引起分子内部应力的增加。每个真实的分子结构, 都是在上述几 种作用达到平衡状态的表现。
“化学键以及由这些键构成的键角等会发生变化, 即出现键的拉伸或压缩、键角的扭 变” 所代表的总能量变化能描述和它有关的 “化学过程”。最重要的是, 这个过程中 你并不需要解薛定谔方程! 所以看上去,你忽略了电子。但其实电子的信息早已经在 势能参数里面了。
这个势能可以叫做当前甲烷的分子动力学 “力场”。有了它,你就可以在波恩一奥本海 默近似下描述原子的运动了。
分子模拟
- 分子模拟将原子、分子按经典粒子处理, 可提 供微观结构、运动过程以及它们与宏观性质相 关的数据和直观图象
- 分子模拟结果取决于所采用的粒子间作用势的 合理、精确程度。又称为 “计算机实验” , 是 理论与真实实验之间的桥梁
分子模拟的两种主要方法:
(1) 分子动力学法 (MD , Molecular Dynamics)一基于粒子 运动的经典轨迹
(2) Monte Carlo法 (MC)一基于统计力学
针对那些有概率分布或概率密度函数的变 量, 我们构建一系列样本集, 使得满足该 种概率条件, 然后每个样本根据具体物理 事件推演, 得到目标的样本集, 最终进行 统计分析, 得到我们需要的目标概率分布 或概率密度函数等。
Metropolis算法一移动然后选择接受这个移动还是拒绝这个移动
- 从起始构型 x ( i ) \mathbf{x}^{(i)} x(i) ,计算能量 E ( i ) E^{(i)} E(i) ;
- 随机移动一些构型坐标得到一个trial构型 x ( i + 1 ′ ) \mathbf{x}^{\left(i+1^{\prime}\right)} x(i+1′) ,并计算该构型的能量 E ( i + 1 ′ ) E^{\left(i+1^{\prime}\right)} E(i+1′) ;
- 决定是否接受这个移动:
(1)如果 E ( i + 1 ′ ) ≤ E ( i ) E^{\left(i+1^{\prime}\right)} \leq E^{(i)} E(i+1′)≤E(i) ,那么100%接受这个移动,正式的下一步构型就是 x ( i + 1 ) = x ( i + 1 ′ ) \mathbf{x}^{(i+1)}=\mathbf{x}^{\left(i+1^{\prime}\right)} x(i+1)=x(i+1′) 了;
(2) 如果 E ( i + 1 ′ ) > E ( i ) E^{\left(i+1^{\prime}\right)}>E^{(i)} E(i+1′)>E(i) ,那么产生一个0到1之间的随机数R,并跟转移概率 w i → i + 1 ′ = exp ( β Δ E i , i + 1 ′ ) w_{i \rightarrow i+1^{\prime}}=\exp \left(\beta \Delta E_{i, i+1^{\prime}}\right) wi→i+1′=exp(βΔEi,i+1′) 比较,如果 w i → i + 1 ′ > R w_{i \rightarrow i+1^{\prime}}>R wi→i+1′>R 那就接受这个移动 x ( i + 1 ) = x ( i + 1 ′ ) \mathbf{x}^{(i+1)}=\mathbf{x}^{\left(i+1^{\prime}\right)} x(i+1)=x(i+1′) ,否则就拒绝这个移动 x ( i + 1 ) = x ( i ) \mathbf{x}^{(i+1)}=\mathbf{x}^{(i)} x(i+1)=x(i) ; - 回到第二步,直到累积 N \mathrm{N} N 个构型。
分子模拟的两种主要方法比较:

1、算法的难易程度。一般说来,
M
D
M D
MD 的算法比
M
C
M C
MC 要复杂一些。这是因为, 对于
M
C
M C
MC 而言, 每产 生一帧新的构型只要计算能量然后根据acceptance ratio移动粒子就足够了。但对于
M
D
M D
MD, 每产生一帧新的构型所需要的不只是能量, 还需要每个粒子的速度和受力来对牛顿运动方程 进行数值积分, 这就加大了计算量。如果还要考虑为了提高计算效率的Verlet neighbor list 等设置,MD的算法会更复杂一些。
2、所能计算性质的多少。很明显,
M
D
M D
MD 能比
M
C
M C
MC 计算更多的性质,
M
C
M C
MC 只能计算一些与动力学无 关的平衡态性质, 比如能量、比热容等等,
M
D
M D
MD 既可以计算与动力学无关的性质, 也可以计算 与动力学相关的性质, 比如扩散系数、热导率、黏度、态与态之间的跃迁速率, 光谱等等。 这是因为, 使用Metropolis算法的MC, 为了快速得到平衡态的分布, 把整个系统简化为一条 马尔可夫链, 第
N
N
N 个构型只和第
N
−
1
N-1
N−1 个构型有关联, 与第
N
−
2
N-2
N−2 或者更早的构型没有什么关联。 在实际情况中不是这样的, 系统是有记忆的, 在
t
0
t_0
t0 时刻处于相空间中
(
p
0
,
q
0
)
\left(p_0, q_0\right)
(p0,q0) 点的系统与在
t
1
t_1
t1 时刻处于
(
p
1
,
q
1
)
\left(p_1, q_1\right)
(p1,q1) 的系统是有关联的, 它们之间的关联可以用条件概率
P
(
p
1
,
q
1
;
t
1
∣
p
0
,
q
0
;
t
0
)
P\left(p_1, q_1 ; t_1 \mid p_0, q_0 ; t_0\right)
P(p1,q1;t1∣p0,q0;t0) 来描述。很多动力学性质都和这样的条件概率有关系, 而MD产生的数据是可以计算这些概率 分布的。所以世界上没有免费的午餐,
M
C
M C
MC 虽然算法简单, 但大体上只能计算静态性质, 如果 要计算动力学性质还是要上MD。
3、可使用的软件。可使用的
M
D
M D
MD 的软件远多于
M
C
M C
MC 的软件。很大程度上是由于
M
D
M D
MD 能够计算 的性质远比
M
C
M C
MC 多, 并且数据可视化后给人更多直观的感受。比如说, 你可以把
M
D
M D
MD 模拟蛋白 质折叠的轨迹文件用软件可视化之后做成动画, 动画就比较直观地演示了蛋白质结构随时间 的变化。可是如果用
M
C
M C
MC 做同样一个体系的模拟, 把轨迹可视化之后看到的可能就是一堆原 子像无头苍蝇一样乱动, 最后稳定在某个构型附近。一般来讲, MD软件的开发也不难, 一 旦把积分牛顿方程的engine写好, 往里面添加新的相互作用势并不难, 这样每添加一点新的 功能, MD软件就可以适用于更多的体系。相比起MD软件的百花齐放, 分子模拟中学术界 通用的
M
C
M C
MC 软件并不多, 很多课题组都是自己写
M
C
M C
MC 代码, 但适用范围仅限于自己研究的体 系。
4、增强抽样 (enhanced sampling)。这是分子模拟中的一个大坑, 不管MD还是MC都会 面临在系综中采样不足的问题。
分子动力学模拟
原理:模拟过程是在一定系统及分子势能函数已知 的条件下,从计算分子间作用力着手,求解 牛顿运动方程,得到每个时刻各个分子的坐 标与动量, 即在相空间的运动轨迹, 再利用 统计计算方法得到多体系统的静态和动态特 性,从而得到系统的宏观性质。因此分子动 力学方法可以看作是体系在一段时间内的发 展过程的模拟。系统的初始位形和初始速度 可以通过实验数据、或理论模型、或两者的 结合来决定。
优势:分子动力学模拟是分子模拟中最接近实验条 件的模拟方法, 能够从原子层面给出体系的 微观演变过程, 直观的展示实验现象发生的 机理与规律, 促使我们的研究向着更高效, 更经济, 更有预见性的方向发展, 因此, 分 子动力学模拟在生物, 药学, 化学, 材料科 学的研究中发挥着越来越重要的作用。
计算机模拟形式
计算机模拟的主要表现形式
- 分子动力学法(MD, Molecular Dynamics ) – 牛顿方程
- 蒙特卡洛法(MC, Monte Carlo) – 郎之万方程
- 量子力学法(Quantum Mechanics) – 薛定谔方程
分子动力学法
在分子动力学法中,设想把 N \mathrm{N} N 个粒子 (可以是原子、分于或离子)的体系放在一个体 积单元(一般是正方体)中,每个粒子的初位置和初速度事先给定,随后的各粒子的运动 状态是按照一定的时间步长 Δ t \Delta \mathbf{t} Δt ,求解牛顿运动方程(对球对称分子)或耦合的牛顿-欧拉运 动方程(对非球对称的刚性分子除平动自由度还有转动自由度)而确定的。
体系的平衡性质, 可用时间平均来计算
⟨
A
⟩
=
1
T
∫
0
T
A
(
t
)
d
t
≈
1
M
∑
m
=
1
M
A
(
m
Δ
t
)
\langle A\rangle=\frac{1}{T} \int_0^T A(t) d t \approx \frac{1}{M} \sum_{m=1}^M A(m \Delta t)
⟨A⟩=T1∫0TA(t)dt≈M1m=1∑MA(mΔt)
式中的 A \mathrm{A} A 可以是动能 (由它可以计算温度值), > > >> >> 表示平均, A \mathrm{A} A 也可以是维里(由它可 计算压强值)等等。上式假定 t = 0 t=0 t=0 时体系处于初步平衡态, T \mathrm{T} T 是足够长的时间,一般是从初 步平衡态开始计算机模拟的整个时间, t t t 为时间步长, m m m 为总步数。可知,除了初条件(座 标、速度)是事先选定输入计算机的外, 原则上讲以后整个的计算过程是完全确定的。
蒙特卡洛法
在蒙特卡洛法中,随机性是本质的。体积单元中
N
\mathrm{N}
N 个粒子的坐标是逐次由计算机控制 而随机变化的,但这种变化是要使体系在相空间中,每个位形出现的频率与特定统计系综 的相应几率密度成正比(例如,对正则系综,几率密度为:
ρ
=
exp
(
−
v
N
k
T
)
\rho=\exp \left(-\frac{v_N}{k T}\right)
ρ=exp(−kTvN)
其中
V
V
V 为体系势能,
k
k
k 为波尔兹曼常数,
T
T
T 为温度。这样, 粒子坐标函数的系综平均(例 如势能或维里)即可作为上述由计算机给出的一系列位形的无权重平均而得到。
就上述意义讲, 在蒙特卡洛模拟中, 各个分子坐标的变动, 并不与分子的实际运动相联系, 它没有明确的物理意义, 只是一种随机取样。一般是采用重要性取样(importance sampling), 即按照一定的几率给出一系列位形。为了得到可靠的结果, 往往要采用
1
0
3
∼
1
0
6
10^3 \sim 10^6
103∼106 个位形。位形出现的先后次序也没有特殊意义。所以用蒙特卡洛法模拟, 所估算的物理量 是对系综平均求的。但随着蒙特卡洛技术的发展,现已在某种意义上把它理解为 “时间”平 均(这里的“时间”只表征一系列状态在先后次序上的标号, 并非物理函义上的时间)。在这 种认识的基础上 发屏了解决非平衡讨程的技术。
量子力学法
量子动力学是相对于经典力学(classical dynamics)的量子形式。“动”是与静相对的, “量 子”则表明本理论的核心框架是使用含时的薛定谔方程。最近几十年,量子动力学得到广 泛的发展,从量子纠细生物发光现象都得到的了广泛的应用。薛定谔方程:
H
φ
=
E
φ
H \varphi=E \varphi
Hφ=Eφ
H
H
H 表示哈密顿算子;
φ
\varphi
φ 表示波函数 ;
E
E
E 表示体系的能量。分子包含电子和原子核, 但是 人们往往忽略了它们在分子运动过程中起到的作用。由于多体的薛定谔方程难解, 量子力 学运用到分子领域直到波恩和其导师提出绝热近似,才让薛定谔解多体问题得到一个大大 的进步。
量子动力学主要应用量子力学的方法研究体系的动量和能量的交换.分子量子动力学, 通常简称为量子动力学,是理论化学的一个分支,特点是分子体系中电子与原子核都用量 子力学方法处理。分子量子动力学可被视为量子物理与化学的结合。分子量子动力学,是 运用含时薛定谔方程为理论框架,研究分子动力学。
分子立场
空间简介
分子力学从几个主要的典型结构参数和作用力出发来讨论分子结构, 即用位能函数 来表示当键长、键角、二面角等结构参数以及非键作用等偏离“理想”值时分子能量(称为 空间能, space energy)的变化。采用优化的方法, 寻找分子空间能处于极小值状态时分 子的构型。
位能函数描述了各种形式的相互作用力对分子位能的影响, 它的有关参数、常数和 表达式通常称为力场。
对于某个分子来说, 空间能是分子构象的函数。由于在分子内部的作用力比较复杂, 作用类型也较多;对于不同类型的体系作用力的情况也有差别。
分子力场原理
分子力场: 在分子体系中, 原子与原子间的相互作用, 用势函数描述.
在分子力学模型中, 每个粒子通常代表一个原子, 在此基础上建立的力场称为全 原子力场。分子力场势能函数来自实验结果的经验公式, 对分子能量的模拟比较 粗粘, 但是相比于精确的量子力学从头计算方法, 分子力场的计算量要小数十倍, 因此对蛋白质复杂体系而言,分子力场方法是一套有效的方法。
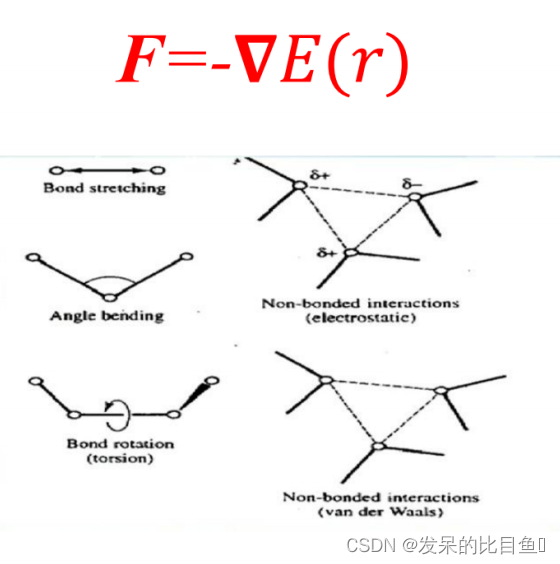
E ( r ) = ∑ bonds K b ( b − b 0 ) 2 + ∑ angles K θ ( θ − θ 0 ) 2 + ∑ dihedrals V n 2 ( 1 + cos [ n ϕ − δ ] ) + ∑ n o n b i j [ ( A i j r i j 12 ) − ( B i j r i j 6 ) + ( q i q j r i j ) ] \begin{aligned} E(r)= & \sum_{\text {bonds }} K_b\left(b-b_0\right)^2+\sum_{\text {angles }} K_\theta\left(\theta-\theta_0\right)^2 \\ & +\sum_{\text {dihedrals }} \frac{V_n}{2}(1+\cos [n \phi-\delta]) \\ & +\sum_{n o n b i j}\left[\left(\frac{A_{i j}}{r_{i j}^{12}}\right)-\left(\frac{B_{i j}}{r_{i j}^6}\right)+\left(\frac{q_i q_j}{r_{i j}}\right)\right] \end{aligned} E(r)=bonds ∑Kb(b−b0)2+angles ∑Kθ(θ−θ0)2+dihedrals ∑2Vn(1+cos[nϕ−δ])+nonbij∑[(rij12Aij)−(rij6Bij)+(rijqiqj)]
分子立场分类
分子动力学模拟结果的准确性主要依赖于模拟中所选用的分子力场 目前常用的分子力场有: CHARMM、AMBER、GROMACS、 OPLS/NAMD等等。
动力学求解
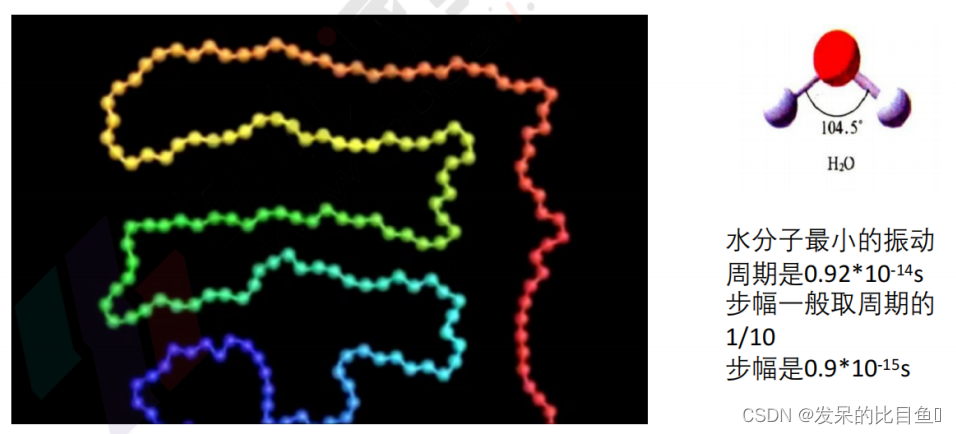
分子动力学模拟中, 分略了量子效应后, 系统中的粒子将遵循牛顿运动定律。为得到原于的运动, 可以采用有限差分方法来求解运动方程。常用的方法有Verlet算法、Leap-frog算法、Velocity Verlet算法等。
有限差分方法的时间步幅的设定是一个重要的问题, 如果太大则 使原子的位置变动太大。一般 (fs 量级) 应该小到足以模拟所有原子 的运动, 也就是要能够计算振动最快的原子的运动。如果做不到这一 点, 则计算分子的内能将是不稳定地, 使计算失败。
有限差分法
有限差分方法的基本思想
把整体的折散成许多小的段, 每一个段通过固定的时间被分隔在时间
t
\mathbf{t}
t 构型中, 每一质点上的总力等于与其它质点相互作用的矢量加和。
有限差值方法在分子动力学计算中步骤
- 设定粒子的初始位置和速度
- 根据粒子的位置计算每个粒子的受力
- 根据粒子的位置、速度和受力计算粒子新位置和新速度
- 更新粒子的位置和速度, 然后回到第2步
初始速度的设定
在计算中各原子的运动初速度的设定是一个重要问题。初速度的设定应与体 系的温度相匹配。系统中各原子的初始速度由初始温度分布下的Maxwell–Boltzmann分布来随机选取。
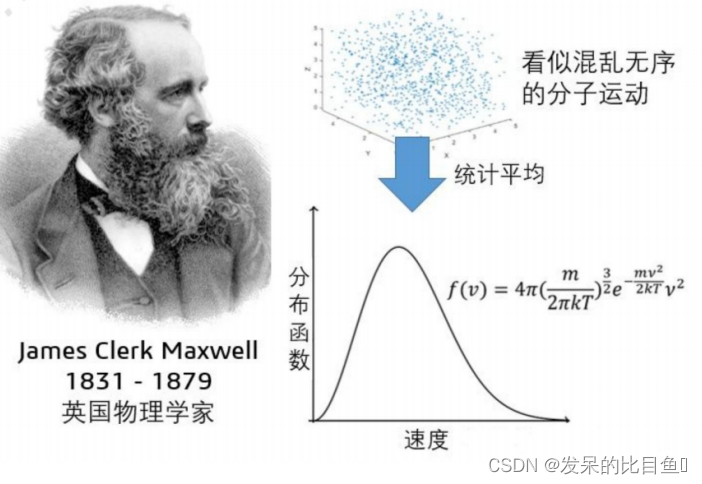
按速度分量的麦克斯韦分布律和分布函数:
f
(
v
x
)
=
(
m
2
π
k
T
)
1
/
2
e
−
m
v
x
2
2
k
T
f\left(v_x\right)=\left(\frac{m}{2 \pi k T}\right)^{1 / 2} e^{-\frac{m v_x^2}{2 k T}}
f(vx)=(2πkTm)1/2e−2kTmvx2
求解动力学方程的数值方法
- Verlet算法
- Leap-frog (蛙跳) 算法
- Velocity-Verlet算法
为了得到原子的运动轨迹, 可以采用差分法求解运动方程。对速度和加速度进 行泰勒级数展开:
r
(
t
+
Δ
t
)
=
r
(
t
)
+
v
(
t
)
Δ
t
+
1
2
a
(
t
)
Δ
t
2
+
⋯
⋯
v
(
t
+
Δ
t
)
=
v
(
t
)
+
a
(
t
)
Δ
t
+
1
2
b
(
t
)
Δ
t
2
+
⋯
⋯
a
(
t
+
Δ
t
)
=
a
(
t
)
+
b
(
t
)
Δ
t
+
⋯
⋯
\begin{gathered} \mathbf{r}(t+\Delta t)=\mathbf{r}(t)+\mathbf{v}(t) \Delta t+\frac{1}{2} \mathbf{a}(t) \Delta t^2+\cdots \cdots \\ \mathbf{v}(t+\Delta t)=\mathbf{v}(t)+\mathbf{a}(t) \Delta t+\frac{1}{2} \mathbf{b}(t) \Delta t^2+\cdots \cdots \\ \mathbf{a}(t+\Delta t)=\mathbf{a}(t)+\mathbf{b}(t) \Delta t+\cdots \cdots \end{gathered}
r(t+Δt)=r(t)+v(t)Δt+21a(t)Δt2+⋯⋯v(t+Δt)=v(t)+a(t)Δt+21b(t)Δt2+⋯⋯a(t+Δt)=a(t)+b(t)Δt+⋯⋯
用粒子在时刻
t
t
t 的坐标和速度以及粒子在 前一时刻
t
−
Δ
t
t-\Delta t
t−Δt 的坐标, 来计算粒子在
t
+
Δ
t
t+\Delta t
t+Δt 时刻的坐标
r
(
t
+
Δ
t
)
=
r
(
t
)
+
Δ
t
v
(
t
)
+
1
2
Δ
t
2
a
(
t
)
+
⋯
⋯
r
(
t
−
Δ
t
)
=
r
(
t
)
−
Δ
v
(
t
)
+
1
2
Δ
t
2
a
(
t
)
+
⋯
⋯
\begin{aligned} \mathbf{r}(t+\Delta t) & =r(t)+\Delta t \mathrm{v}(t)+\frac{1}{2} \Delta t^2 \mathbf{a}(t)+\cdots \cdots \\ \mathbf{r}(t-\Delta t) & =\mathbf{r}(t)-\Delta \mathbf{v}(t)+\frac{1}{2} \Delta t^2 \mathbf{a}(t)+\cdots \cdots \end{aligned}
r(t+Δt)r(t−Δt)=r(t)+Δtv(t)+21Δt2a(t)+⋯⋯=r(t)−Δv(t)+21Δt2a(t)+⋯⋯
把这两个方程相加减并忽略高级项, 得到:
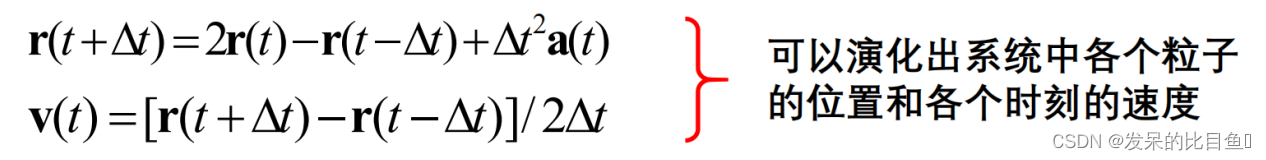
Verlet算法
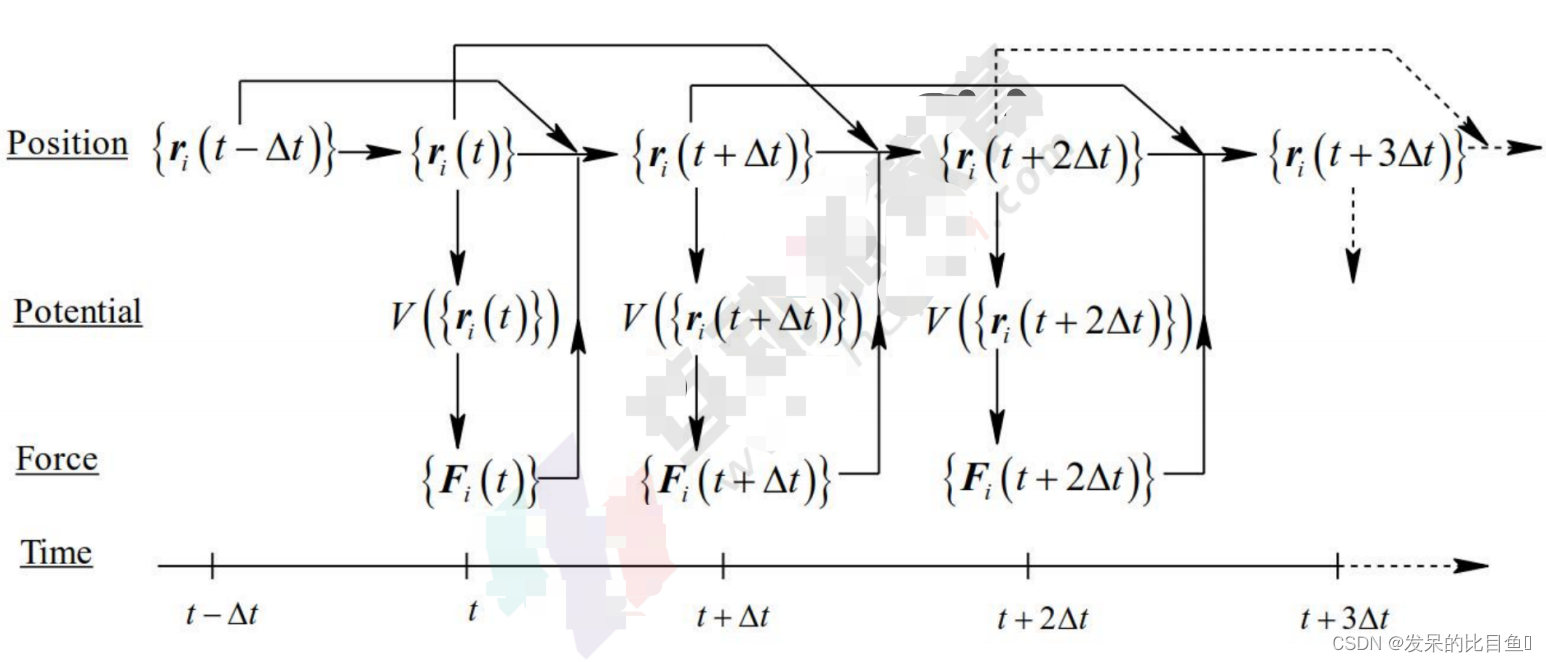
r
(
t
+
δ
t
)
=
r
(
t
)
+
d
d
t
r
(
t
)
δ
t
+
1
2
!
d
2
d
t
2
r
(
t
)
(
δ
t
)
2
+
…
r
(
t
−
δ
t
)
=
r
(
t
)
−
d
d
t
r
(
t
)
δ
t
+
1
2
!
d
2
d
t
2
r
(
t
)
(
δ
t
)
2
+
…
\begin{aligned} & r(t+\delta t)=r(t)+\frac{d}{d t} r(t) \delta t+\frac{1}{2 !} \frac{d^2}{d t^2} r(t)(\delta t)^2+\ldots \\ & r(t-\delta t)=r(t)-\frac{d}{d t} r(t) \delta t+\frac{1}{2 !} \frac{d^2}{d t^2} r(t)(\delta t)^2+\ldots \end{aligned}
r(t+δt)=r(t)+dtdr(t)δt+2!1dt2d2r(t)(δt)2+…r(t−δt)=r(t)−dtdr(t)δt+2!1dt2d2r(t)(δt)2+…
两式相加, 忽略高阶小量
r
(
t
+
δ
t
)
=
−
r
(
t
−
δ
t
)
+
2
r
(
t
)
+
d
2
d
t
2
r
(
t
)
(
δ
t
)
2
r(t+\delta t)=-r(t-\delta t)+2 r(t)+\frac{d^2}{d t^2} r(t)(\delta t)^2
r(t+δt)=−r(t−δt)+2r(t)+dt2d2r(t)(δt)2
两式相减, 忽略高阶小量, 除以
2
δ
t
2 \delta t
2δt
v
(
t
)
=
d
r
d
t
=
1
2
δ
t
[
r
(
t
+
δ
t
)
−
r
(
t
−
δ
t
)
]
v(t)=\frac{d r}{d t}=\frac{1}{2 \delta t}[r(t+\delta t)-r(t-\delta t)]
v(t)=dtdr=2δt1[r(t+δt)−r(t−δt)]
分子动力学
Verlet算法 - 应用最为广泛, 计算简明扼要, 但是精度较差, 没有显式速度项, 需要下一步的坐标计算速度。
Leap-frog-Verlet(蛙跳)算法 - Verlet算法的一种变化形式, 轨迹与前者完全一 样, 计算量较小, 包含显式速度项, 但是速度 与位置计算不同步。
Velocity-Verlet算法 Velocity-Verlet算法是Verlet算法的另一种变化形 式, 计算量适中, 可以同时给出位置, 速度和 加速度, 目前应用比较广泛。
时间步长选择
步长太小,轨迹将覆盖, 只有一个限定的相空间性质;
步长太大, 不稳定性在积分算法中可能升高, 由于原子间高能重叠。导致能量和 线性动量守恒的破坏
系统理论
系综( ensemble )代表一大群相类似的体系的集合。对一类相同性质的体 系, 其微观状态(比如每个粒子的位置和速度)仍然可以大不相同。 (实际上, 对于一个宏观体系, 所有可能的微观状态数是天文数字。)统计物理的一个基 本假设(各态历经假设)是:对于一个处于平衡的体系, 物理量的时间平均, 等 于对对应系综里所有体系进行平均的结果。体系的平衡态的物理性质可以对 不同的微观状态求和来得到。系综的概念是由约西亚. 威拉德-吉布斯 (J.Willard Gibbs) 在 1878 年提出。
常用系综:
微正则系综(microcanonical ensemble, NVE)
正则系综(canonical ensemble, NVT)
巨正则系综(grand canonical ensemble,
μ
V
T
)
\mu VT)
μVT)
等温等压系综(isothermal-isobaric ensemble, NPT)
等压等焓系综(contant-pressure,constant-enthalpy, NPH)
微正则系综(microcanonical ensemble, NVE): _系综里的每个体系具有相同 的能量(通常每个体系的粒子数和体积也是相同的)。
正则系综(canonical ensemble, NVT): 系综里的每个体系都可以和其他体系 交换能量(每个体系的粒子数和体积仍然是固定且相同的),但是系综里所 宥体系的能量总和是固定的。系综内各体系有相同的温度。
巨正则系综 (grand canonical ensemble,
μ
V
T
\mu \mathrm{VT}
μVT ): 正则系综的推广, 每个体 系都可以和其他体系交换能量和粒子, 但系综内各体系的能量总和以及粒子 数总和都是固定的… (系综内各体系的体积相同。)系综内各个体系有相同的温 度和化学势。
等温等压系综(isothermal-isobaric ensemble, NPT): 正则系综的推广,体系 间可交换能量和体积, 但能量总和以及体积总和都是固定的。(系综内各体系 有相同的粒子数。)正如它的名字, 系综内各个体系有相同的温度和压强。