H. Visit the Park(STL)

题意：给你一个无向图，每条边上都有一个数码，然后给你一个路径，每次你必须从Ai走到Ai+1（直接走到，必须相邻），如果有多条路径，你等概率的选择这些路径，这样从头走到尾，你依次把这些数码写下来，得到一个十进制数，现在问你最后可以得到的期望是多少？
思路：我们可以单独考虑每一位的贡献，个位上的某种在所有从左到右写下来的数的个位的占比仅和个位自身各种数码的比例有关，尽管高其他位右各种选择，但是个位上出现这个数码的概率是相同的。利用map我们维护总数，和各种数码出现的次数。
注意：这里容易被卡常，我们可以发现求逆元的常数为30，加上10个数码，如果放到循环內部的话，就是300，再乘上3e5，9e7加上其他常数，tle4了。所以必须放外面。logn最多是20，常数小1.5倍。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 3e5 + 5, mod = 998244853;
map<pair<int, int>, int> g[N];//这是一个map<pair<int,int>, int>为元素的数组
map<pair<int, int>, int> sum;
ll po(ll rad, ll idx) {
	ll res = 1;
	while (idx) {
		if (idx & 1) res = res * rad % mod;
		rad = rad * rad % mod;
		idx >>= 1;
	}
	return res;
}
int a[N];
void solve() {
	int n, m, k;
	cin >> n >> m >> k;
	for (int i = 0; i < m; i++) {
		int u, v, w;
		cin >> u >> v >> w;
		g[u][{v, w}]++;
		g[v][{u, w}]++;
		sum[{u, v}]++;
		sum[{v, u}]++;
	}
	for (int i = 1; i <= k; i++) cin >> a[i];
	ll ans = 0;
	for (int i = k; i > 1; i--) {
		int u = a[i], v = a[i - 1];
		int ss = sum[{u, v}];
		if (!ss) {
			cout << "Stupid Msacywy!\n";
			return;
		}
		ll mul = po(10, k - i), sub = po(ss, mod - 2);//这里很重要 
		for (int j = 1; j <= 9; j++) {
			if (g[u].count({v, j})) ans = (ans + mul * j % mod * g[u][{v, j}] % mod * sub % mod) % mod; 
		}
	}
	cout << ans << '\n';
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

G. Matrix Repair(思维题)

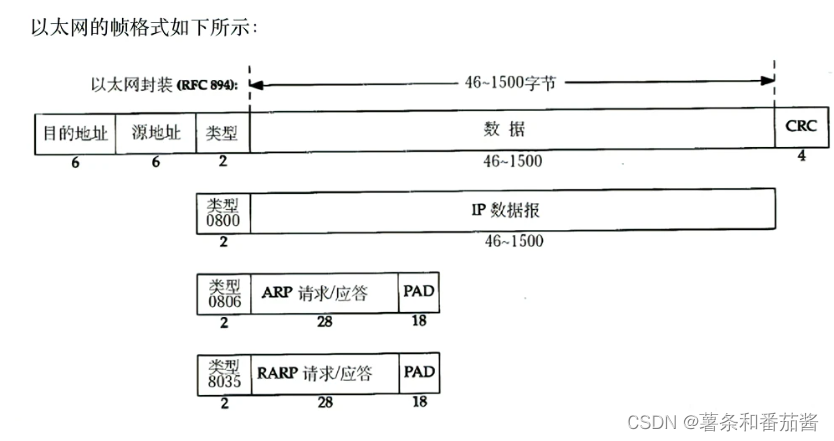
背景：在数据传输当中常见的奇偶性检查
题意：给你一个破损的矩阵，给你原来的矩阵的行列的奇偶性，让你复原这个矩阵，如果矩阵唯一，就输出这个矩阵，如果矩阵不唯一，就输出-1。
思路：（借用oiwiki的图）
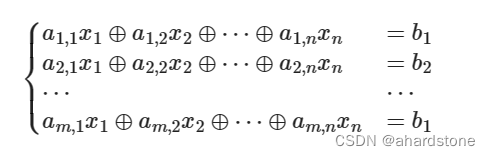
在这里插入图片描述
我们如果把所有-1处和所在的行列列出方程，我们可以发现，如果说任何一行一列都不存在只有一个-1的情况，那么每条方程，至少有两个未知数。对于不同行，不同列，这些方程最多只有一个相同的未知元。（也就是某行和某列相交的情况有一个相同的未知元（-1）），因此我们无法通过加减消元解出任何一个确定的未知元，无论如何消元都至少有两个未知元。因此我们拓扑排序，逐步带入某个确定的未知元即可。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
const int N = 1005, mod = 998244853;
int a[N][N], r[N], c[N], nr[N], nc[N];
set<int> g[N << 1];
void solve() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cin >> a[i][j];
		}
	}
	for (int i = 1; i <= n; i++) {
		cin >> nr[i];
		int s = 0;
		for (int j = 1; j <= n; j++) {
			if (a[i][j] == -1) {
				g[i].insert(j);
				continue;
			}
			s ^= a[i][j];
		}
		r[i] = s;
	}
	for (int j = 1; j <= n; j++) {
		cin >> nc[j];
		int s = 0;
		for (int i = 1; i <= n; i++) {
			if (a[i][j] == -1) {
				g[j + n].insert(i);
				continue;
			}
			s ^= a[i][j];
		}
		c[j] = s;
	}
	set<pair<int, int>> st;
	for (int i = 1; i <= n * 2; i++) {
		st.insert({g[i].size(), i});
	}
	while (!st.empty()) {
		pair<int, int> pii = *st.begin();
		int fi = pii.first, se = pii.second;
		st.erase(st.begin());
		if (fi == 0) continue;
		if (fi != 1) break;
		if (se > n) {//如果是某列的话 
			int x = *g[se].begin();//该列含有的唯一的-1 
			g[se].erase(g[se].begin());//删除-1 
			st.erase({g[x].size(), x});//-1所在行删除 
			int y = se - n;//对应列 
			g[x].erase(y);//对应行删除本列
			st.insert({g[x].size(), x});//更新对应行 
			a[x][y] = c[y] ^ nc[y];//填数字 
			c[y] = nc[y];//更新列 
			r[x] ^= a[x][y];//更新行 
		} else {
			int y = *g[se].begin();//该行含有的唯一的-1 
			g[se].erase(g[se].begin());//删除-1 
			int x = se;//对应行 
			st.erase({g[y + n].size(), y + n});//删除对应列,这里要+n 
			g[y + n].erase(x);
			st.insert({g[y + n].size(), y + n});//更新对应列 
			a[x][y] = r[x] ^ nr[x];//更新 
			r[x] = nr[x];
			c[y] ^= a[x][y];
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			if (a[i][j] == -1) {
				cout << -1 << '\n';
				return;
			}
		}
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			cout << a[i][j] << " \n"[j == n];
		}
	}
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}

C.Random Number Generator(BSGS算法)

题意：给定x0,a,b,m，问利用线性同余方法xi+1=axi+b（mod m）判断某个数是否在xn的集合内。
思路：参考这篇
补充一下如何求出等比式子，待定系数法。
$AX_{n+1}+B=a(AX_n+B)$
$AX_{n+1}=aAX_n+aB-B=AaX_{n}+Ab$
$A=1,B=\frac{b}{a-1}$
评论：BSGS就是暴力根号分治加哈希。
关于特判：a= 1的时候b=0的时候是no，注意不要使用 a- 1作为逆元，0逆元会把人橄榄。

#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define eps 1e-9
using namespace std;
ll a, b, x0, m, x;
ll po(ll rad, ll idx) {
	ll res = 1;
	while (idx) {
		if (idx & 1) res = res * rad % m;
		rad = rad * rad % m;
		idx >>= 1;
	}
	return res;
}
ll bsgs(ll a, ll b) {
	map<ll, ll> mp;
	ll cur = 1, t = sqrtl(m) + 1;
	for (int B = 1; B <= t; B++) {
		cur = cur * a % m;
		mp[cur * b % m] = B;
	}
	ll now = cur;
	for (int A = 1; A <= t; A++) {
		if (mp.count(now)) return A * t - mp[now];
		now = now * cur % m;
	}
	return -1;
}
void solve() {
	cin >> a >> b >> m >> x0 >> x;
	if (x == x0) {
		cout << "YES\n";
		return;
	}
	if (a == 0) {
		cout << (x == b % m ? "YES\n" : "NO\n");
		return;
	}
	if (a == 1) {
		if (b == 0) {
			cout << "NO\n";
			return;
		} 
	}
	ll aa = a;
	ll bb = (x * (a - 1) + b % m) % m * po((x0 * (a - 1) + b) % m, m - 2) % m;
	cout << (bsgs(aa, bb) == -1 ? "NO\n" : "YES\n");
}
int main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	int T = 1;
//	cin >> T;
	while (T--) {
		solve();
	}
	return 0;
}