1.组合
- 1.77. 组合
- 2.216. 组合总和 III
- 3.17. 电话号码的字母组合
- 4.39. 组合总和
- 5.40. 组合总和 II
2.分割
- 1.131. 分割回文串
- 2.*93. 复原 IP 地址
3.子集
- 1.78. 子集
- 2.90. 子集 II
4.排列
- 1.46. 全排列
- 2.47. 全排列 II
5.棋盘问题
- 1.51. N 皇后
- 2.37. 解数独
6.其他
- 1.491. 递增子序列

1.组合

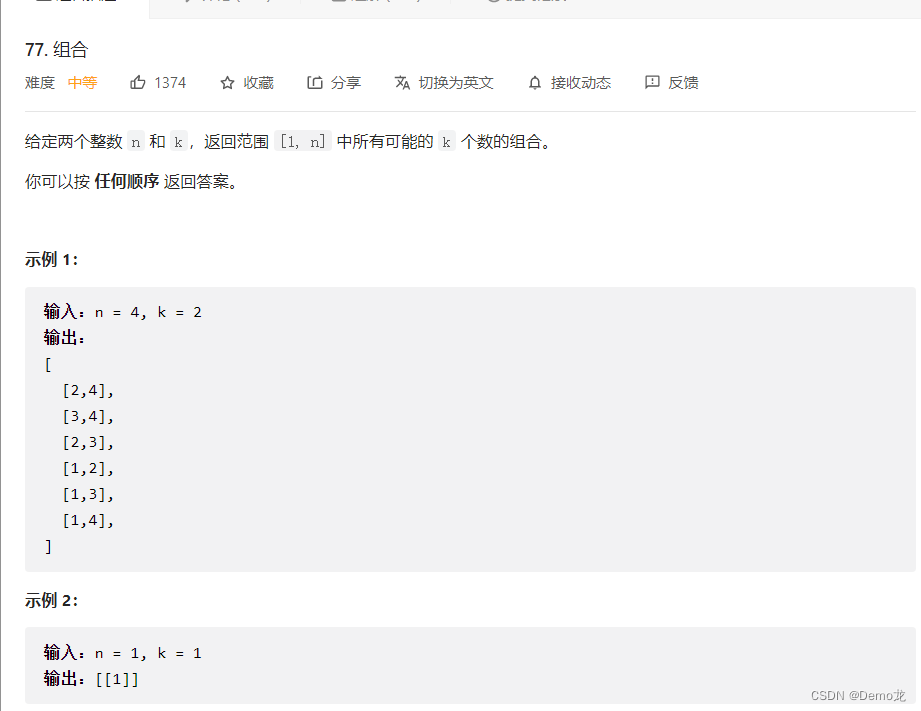
1.77. 组合

链接: 77. 组合
在这里插入图片描述

class Solution {
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    public void tracking(int n,int k,int start){
        if(n-start+1<(k-path.size())){//剪枝操作
            return;
        }
        if(path.size()==k){
            List<Integer> temp=new ArrayList<Integer>(path);
            result.add(temp);
            return;
        }
        for(int i=start;i<=n;i++){
            path.add(i);
            tracking(n,k,i+1);
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> combine(int n, int k) {
        tracking(n,k,1);
        return result;
    }
}

2.216. 组合总和 III

链接: 216. 组合总和 III
在这里插入图片描述

class Solution {
    int sum=0;
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    public void tracking(int n,int k,int start,int sum){
        if(sum>n){//剪枝操作
            return;
        }
        if(path.size()==k&&n==sum){
            List<Integer> temp=new ArrayList<Integer>(path);
            result.add(temp);
            return;
        }
        for(int i=start;i<=9;i++){
            sum+=i;
            path.add(i);
            tracking(n,k,i+1,sum);
            sum-=i;
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> combinationSum3(int k, int n) {
        tracking(n,k,1,sum);
        return result;
    }
}

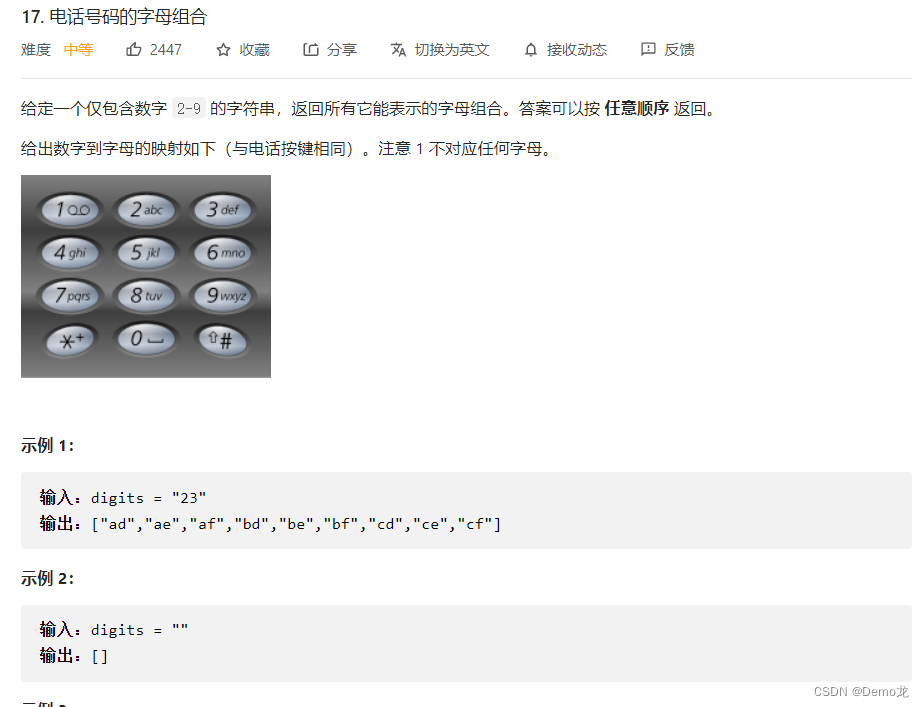
3.17. 电话号码的字母组合

链接: 17. 电话号码的字母组合
在这里插入图片描述

class Solution {
    //定义全局变量
    //定义一个字符串集合存放结果
    List<String> list=new ArrayList<>();
    //字符需要多次添加删除使用StringBuilder存放临时字符串
    StringBuilder temp=new StringBuilder();


    public List<String> letterCombinations(String digits) {
        if(digits==null||digits.length()==0){//如果digits为空
            return list;
        }
        //定义每个数字对应的字符串
        String numString[]={"","","abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        backTracking(digits,numString,0);
        return list;
    }
    
    //index记录数字序列，每次调用函数index+1
    public void backTracking(String digits,String[] numString,int index){
        if(index==digits.length()){//到达叶子结点
            list.add(temp.toString());
            return;
        }
        int num=digits.charAt(index)-'0';// 将index指向的数字转为int
        String words=numString[num];//获得index对应字符串
        for(int i=0;i<words.length();i++){
            temp.append(words.charAt(i));// 处理
            backTracking(digits,numString,index+1);// 递归，注意index+1，下层要处理下⼀个数字了
            temp.deleteCharAt(temp.length()-1);//回溯
        }
    }
}

4.39. 组合总和

链接: 39. 组合总和
在这里插入图片描述
注：使用剪枝必须对原数组进行排序

class Solution {
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    //int sum=0;
    public void tracking(int[] candidates,int target,int sum,int strat){
        
        if(sum>target){
            return;
        }
        if(sum==target){
            List<Integer> temp=new ArrayList<Integer>(path);
            result.add(temp);
            return;
        }
        for(int i=strat;i<candidates.length;i++){
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target)//使用剪枝必须对candidates进行排序
                return;
            path.add(candidates[i]);
            sum+=candidates[i];
            tracking(candidates,target,sum,i);
            sum-=candidates[i];
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
    	 // 排序是剪枝的前提
        Arrays.sort(candidates);
        tracking(candidates,target,0,0);
        return result;
    }
}

5.40. 组合总和 II

链接: 40. 组合总和 II
在这里插入图片描述


class Solution {
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    //int sum=0;
    public void tracking(int[] candidates,int target,int sum,int strat,boolean used[]){
        
        if(sum>target){
            return;
        }
        if(sum==target){
            List<Integer> temp=new ArrayList<Integer>(path);
            result.add(temp);
            return;
        }
        for(int i=strat;i<candidates.length;i++){
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target)//使用剪枝必须对candidates进行排序
                return;
            // used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
            // used[i - 1] == false，说明同一树层candidates[i - 1]使用过
            // 要对同一树层使用过的元素进行跳过
            if (i>0&&candidates[i]==candidates[i-1] &used[i - 1] == false) {
                continue;
            }
            path.add(candidates[i]);
            sum+=candidates[i];
            used[i]=true;
            // 和39.组合总和的区别1，这里是i+1，每个数字在每个组合中只能使用一次
            tracking(candidates,target,sum,i+1,used);
            used[i]=false;
            sum-=candidates[i];
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    	 // 排序是剪枝的前提
         // ⾸先把给candidates排序，让其相同的元素都挨在⼀起。
        Arrays.sort(candidates);
        boolean used[]=new boolean[candidates.length];
        tracking(candidates,target,0,0,used);
        return result;
    }
}

2.分割

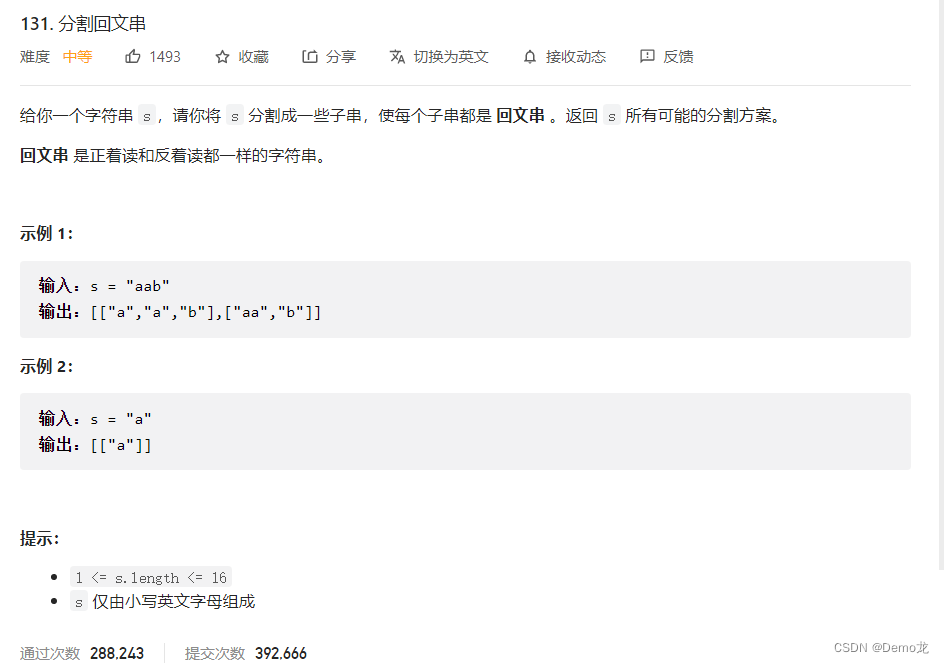
1.131. 分割回文串

链接: 131. 分割回文串
在这里插入图片描述

class Solution {
    List<List<String>>result=new ArrayList<>();
    List<String> path = new ArrayList<>();// 放已经回⽂的⼦串
    //回溯函数
    public void backTracking(String s,int startIndex) {
        // 如果起始位置已经⼤于s的⼤⼩，说明已经找到了⼀组分割⽅案了
        if(startIndex>=s.length()){
            result.add(new ArrayList(path));
            return;
        }
        for(int i=startIndex;i<s.length();i++){
            if(isPalindrome(s,startIndex,i)){// 是回⽂⼦串
                // 获取[startIndex,i]在s中的⼦串
                String str=s.substring(startIndex,i+1);
                path.add(str);
            }else{// 不是回⽂，跳过
                continue;
            }
            backTracking( s,i+1); // 寻找i+1为起始位置的⼦串
            path.remove(path.size()-1); // 回溯过程，弹出本次已经填在的⼦串
        }

    }
    //判断是否是回文串
    public boolean isPalindrome(String s,int start,int end){
        for(int i=start,j=end;i<j;i++,j--){
            if(s.charAt(i)!=s.charAt(j)){
                return false;
            }
        }
        return true;
    }
    public List<List<String>> partition(String s) {
        backTracking(s,0);
        return result;
    }
}

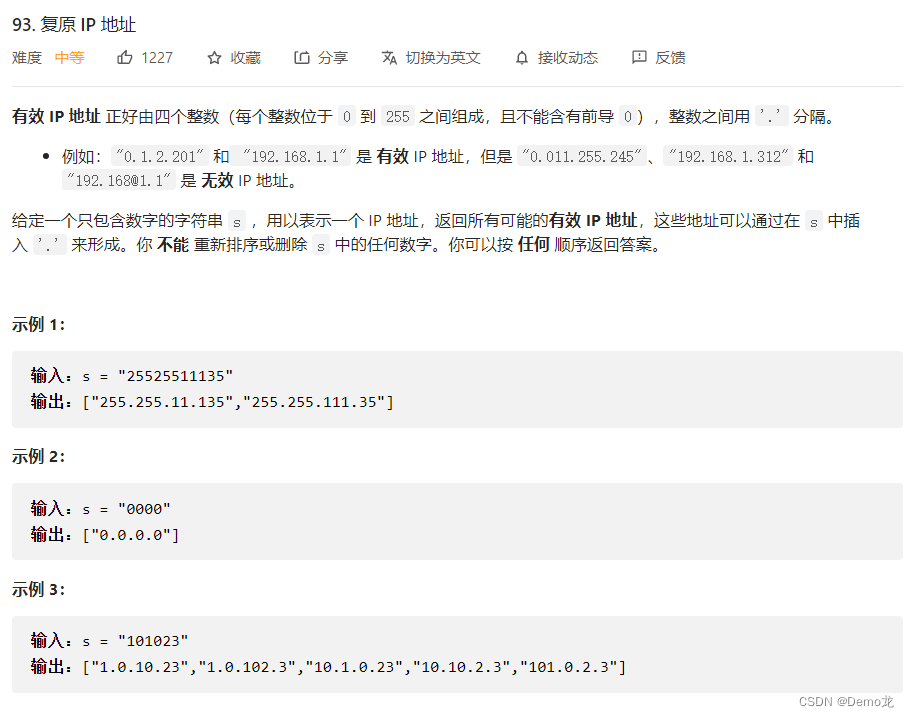
2.*93. 复原 IP 地址

链接: 93. 复原 IP 地址
在这里插入图片描述

class Solution {
    List<String> result = new ArrayList<>();

    public List<String> restoreIpAddresses(String s) {
        if (s.length() > 12) return result; // 算是剪枝了
        backTrack(s, 0, 0);
        return result;
    }

    // startIndex: 搜索的起始位置， pointNum:添加逗点的数量
    private void backTrack(String s, int startIndex, int pointNum) {
        if (pointNum == 3) {// 逗点数量为3时，分隔结束
            // 判断第四段⼦字符串是否合法，如果合法就放进result中
            if (isValid(s,startIndex,s.length()-1)) {
                result.add(s);
            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) {
                s = s.substring(0, i + 1) + "." + s.substring(i + 1);    //在str的后⾯插⼊⼀个逗点
                pointNum++;
                backTrack(s, i + 2, pointNum);// 插⼊逗点之后下⼀个⼦串的起始位置为i+2
                pointNum--;// 回溯
                s = s.substring(0, i + 1) + s.substring(i + 2);// 回溯删掉逗点
            } else {
                break;
            }
        }
    }

    // 判断字符串s在左闭⼜闭区间[start, end]所组成的数字是否合法
    private Boolean isValid(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到⾮数字字符不合法
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) { // 如果⼤于255了不合法
                return false;
            }
        }
        return true;
    }
}

3.子集

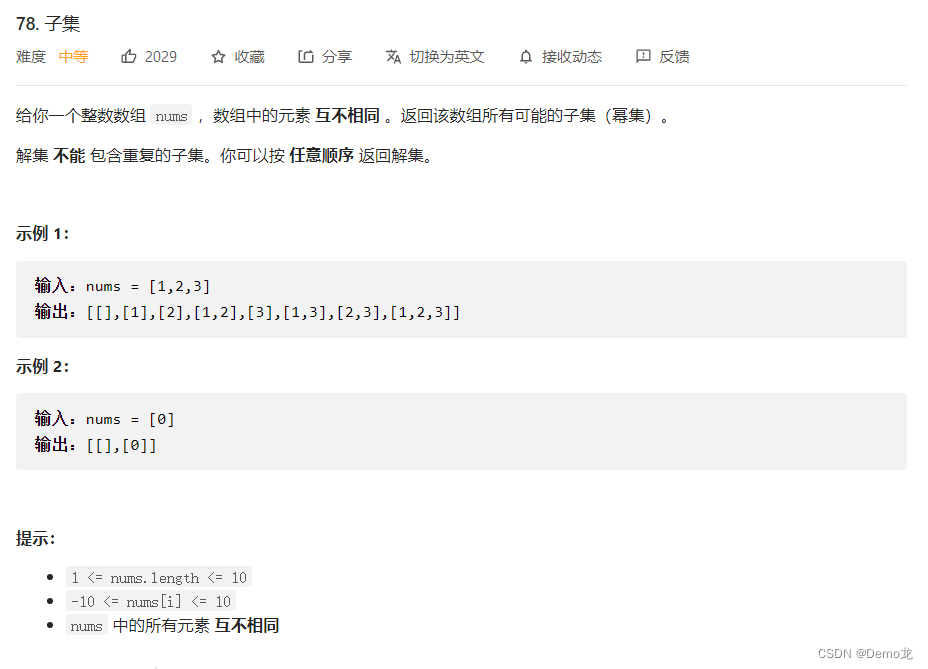
1.78. 子集

链接: 78. 子集
在这里插入图片描述

class Solution {
    List<List<Integer>>result=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public void backTracking(int []nums,int startIndex){
        // 收集⼦集，要放在终⽌添加的上⾯，否则会漏掉⾃⼰{}
        result.add(new ArrayList<Integer>(path));
        if(startIndex>=nums.length){// 终⽌条件可以不加
            return;
        }
        for(int i=startIndex;i<nums.length;i++){
            path.add(nums[i]);//处理节点;
            backTracking(nums,i+1);//递归
            path.remove(path.size()-1);//回溯
        }
    }
    public List<List<Integer>> subsets(int[] nums) {
        backTracking(nums,0);
        return result;
    }
}

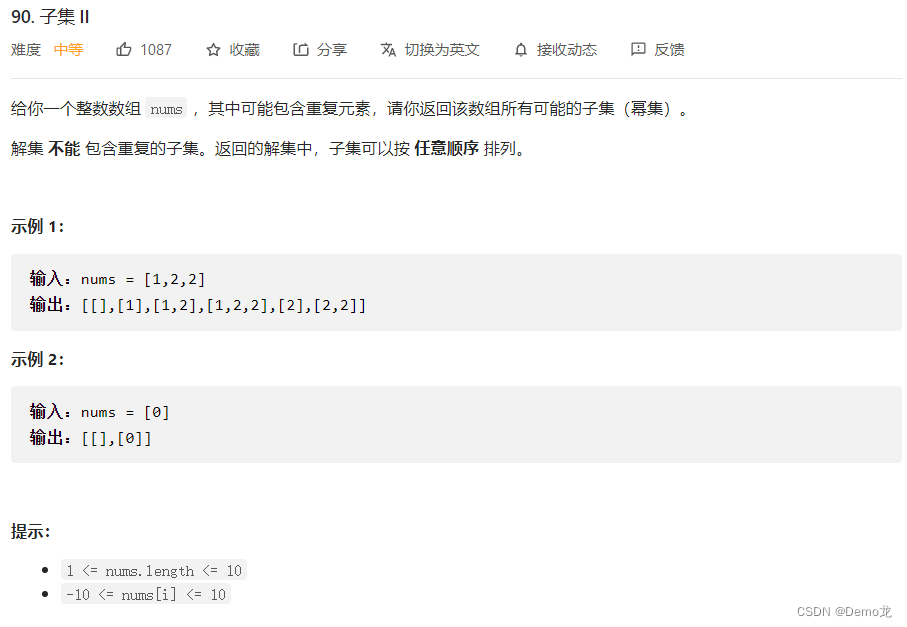
2.90. 子集 II

链接: 90. 子集 II
在这里插入图片描述

class Solution {
    List<List<Integer>>result=new ArrayList<>();
    List<Integer>path=new ArrayList<>();
    public void backTracking(int []nums,int startIndex,boolean []used){
        // 收集⼦集，要放在终⽌添加的上⾯，否则会漏掉⾃⼰{}
        result.add(new ArrayList<Integer>(path));
        if(startIndex>=nums.length){// 终⽌条件可以不加
            return;
        }
        for(int i=startIndex;i<nums.length;i++){
            // 对同一树层使用过的元素进行跳过
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false)
            // 如果发现出现过就pass
                continue;
            used[i]=true;
            path.add(nums[i]);//处理节点;
            backTracking(nums,i+1,used);//递归
            path.remove(path.size()-1);//回溯
            used[i]=false;
        }
    }
    public List<List<Integer>> subsetsWithDup(int[] nums) {
        boolean used[]=new boolean[nums.length];
        Arrays.sort(nums);//这里的排序是去重的关键
        backTracking(nums,0,used);
        return result;
    }
}

4.排列

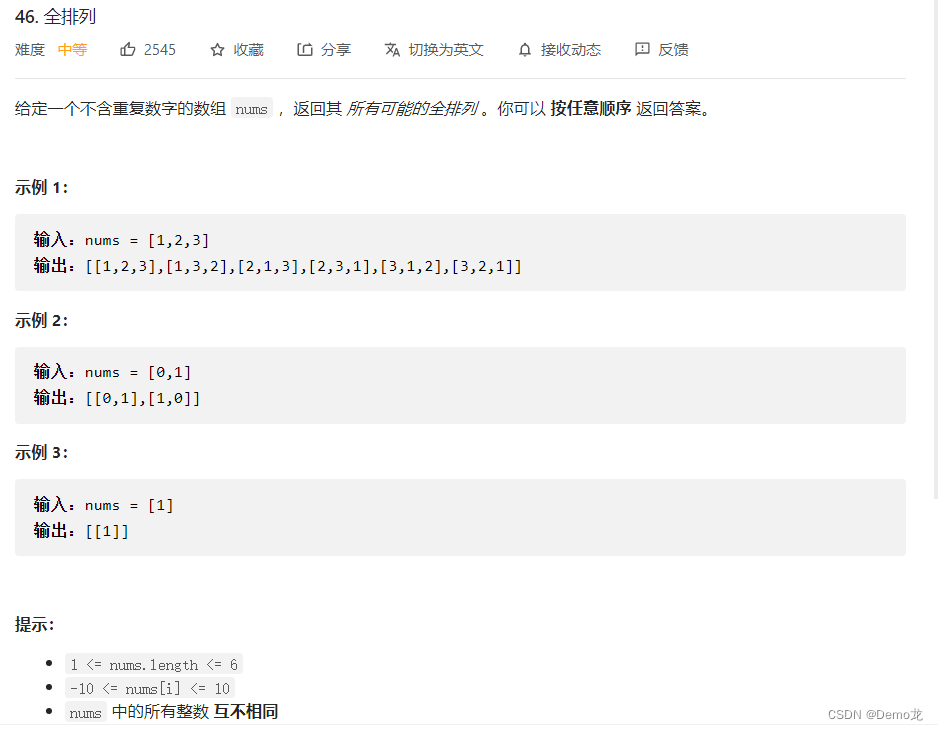
1.46. 全排列

链接: 46. 全排列
在这里插入图片描述

class Solution {
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    public void backTracking(int []nums,boolean used[]){
        if(path.size()==nums.length){// 此时说明找到了一组
            result.add(new ArrayList<Integer>(path));
            return;
        }
        for(int i=0;i<nums.length;i++){
            if(used[i]==true){
                continue;// path里已经收录的元素，直接跳过
            }
            path.add(nums[i]);
            used[i]=true;
            backTracking(nums,used);
            used[i]=false;
            path.remove(path.size()-1);
        }
    }
    public List<List<Integer>> permute(int[] nums) {
        boolean used[]=new boolean[nums.length];
        backTracking(nums,used);
        return result;
    }
}

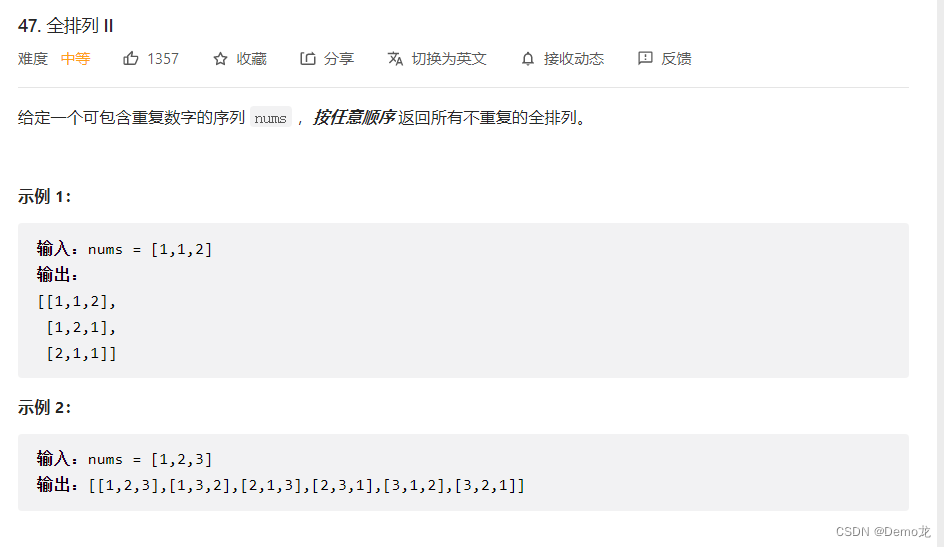
2.47. 全排列 II

链接: 47. 全排列 II
在这里插入图片描述

class Solution {
    List<List<Integer>> result=new ArrayList<List<Integer>>();
    List<Integer> path=new ArrayList<Integer>();
    public void backTracking(int []nums,boolean used[]){
        if(path.size()==nums.length){// 此时说明找到了一组
            result.add(new ArrayList<Integer>(path));
            return;
        }
        for(int i=0;i<nums.length;i++){
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过
            // used[i - 1] == false，说明同⼀树层nums[i - 1]使⽤过
            if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false){
                continue;//树层去重（同一层取过的元素不能再取）
            }
            if(used[i]==true){
                continue;// path里已经收录的元素，直接跳过
            }
            path.add(nums[i]);
            used[i]=true;
            backTracking(nums,used);
            path.remove(path.size()-1);//回溯，
            used[i]=false;//说明同⼀树层nums[i]使⽤过，防止下一树层重复
        }
    }
    public List<List<Integer>> permuteUnique(int[] nums) {
        Arrays.sort(nums);//排序，数层去重的前提
        boolean used[]=new boolean[nums.length];
        backTracking(nums,used);
        return result;
    }
}

5.棋盘问题

1.51. N 皇后

链接: 51. N 皇后
在这里插入图片描述

class Solution {
    List<List<String>>res=new ArrayList<>();
    public List<List<String>> solveNQueens(int n) {
        char [][]chessboard=new char[n][n];
        for(char[]c:chessboard){
            Arrays.fill(c,'.');
        }
        backTrack(n,0,chessboard);
        return res;
    }
    // n 为输入的棋盘大小
    // row 是当前递归到棋盘的第几行了
    public void backTrack(int n,int row,char[][]chessboard){
        if(n==row){
            res.add(Array2List(chessboard));
        }
        for(int col=0;col<n;col++){// 验证合法就可以放
            if(isValid(row,col,n,chessboard)){
                chessboard[row][col]='Q';// 放置皇后
                backTrack(n,row+1,chessboard);
                chessboard[row][col]='.';// 回溯，撤销皇后
            }
        }
    }
    public boolean isValid(int row,int col,int n,char[][]chessboard){
        //判断列
        for(int i=0;i<row;i++){
            if(chessboard[i][col]=='Q'){
                return false;
            }
        }
        //判断45°角
        for(int i=row-1,j=col-1;i>=0&&j>=0;i--,j--){
            if(chessboard[i][j]=='Q'){
                return false;
            }
        }
        //判断135°角
        for(int i=row-1,j=col+1;i>=0&&j<n;i--,j++){
            if(chessboard[i][j]=='Q'){
                return false;
            }
        }
        return true;
    }
    public List<String> Array2List(char[][]chessboard){
        List<String> list=new ArrayList<>();
        for(char []c:chessboard){
            String str=String.copyValueOf(c);
            list.add(str);
        }
        return list;
    }
}

2.37. 解数独

链接: 37. 解数独
在这里插入图片描述

class Solution {
    public void solveSudoku(char[][] board) {
        backTracking(board);
    }
    public boolean backTracking(char[][]board){
        //「一个for循环遍历棋盘的行，一个for循环遍历棋盘的列，
        // 一行一列确定下来之后，递归遍历这个位置放9个数字的可能性！」
        int len=board.length;
        for(int i=0;i<len;i++){// 遍历行
            for(int j=0;j<len;j++){// 遍历列
                if(board[i][j]!='.')// 跳过原始数字
                    continue;
                for(char val='1';val<='9';val++){
                    if(isValid(board,i,j,val)){// (i, j) 这个位置放val是否合适
                        board[i][j]=val;
                        if(backTracking(board)){// 如果找到合适一组立刻返回
                            return true;
                        }
                        //backTracking(board);//递归
                        board[i][j]='.';//回溯
                    }
                }
                // 9个数都试完了，都不行，那么就返回false
                return false;
                // 因为如果一行一列确定下来了，这里尝试了9个数都不行，说明这个棋盘找不到解决数独问题的解！
                // 那么会直接返回， 「这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去！」
            }
        }
        // 遍历完没有返回false，说明找到了合适棋盘位置了
        return true;
    }
    
    public boolean isValid(char[][]board,int row,int col,char val){
        int len=board.length;
        for(int i=0;i<len;i++){
            if(board[row][i]==val){//判断行有无重复
                return false;
            }
            if(board[i][col]==val){//判断列有无重复
                return false;
            }
        }
        
        int startRow=(row/3)*3;//计算3*3宫格的起始位
        int startCol=(col/3)*3;
        for(int i=startRow;i<startRow+3;i++){
            for(int j=startCol;j<startCol+3;j++){
                if(board[i][j]==val){// 判断3*3的9方格里是否重复
                    return false;
                }
            }
        }
        return true;
    }
}

6.其他

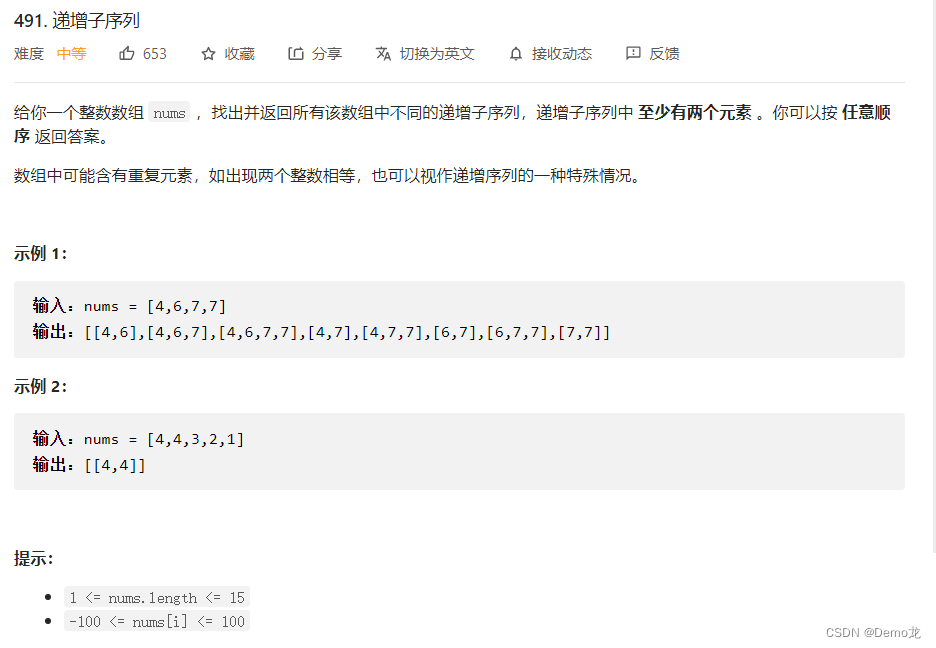
1.491. 递增子序列

链接: 491. 递增子序列
在这里插入图片描述

class Solution {
    private List<Integer> path = new ArrayList<>();
    private List<List<Integer>> result = new ArrayList<>();
    public void backTracking(int []nums,int startIndex){
        // 收集⼦集
        if(path.size()>1){
            result.add(new ArrayList<>(path));
            // 注意这里不要加return，要取树上的节点
        }
    
        int used[]=new int[201];// 使用used对本层元素进行去重

        for(int i=startIndex;i<nums.length;i++){
            // 对同一树层使用过的元素进行跳过
            if((used[nums[i]+100]==1)||!path.isEmpty()&&nums[i]<path.get(path.size()-1))
                continue;
            used[nums[i]+100]=1;// 记录这个元素在本层用过了，本层后面不能再用了
            path.add(nums[i]);//处理节点;
            backTracking(nums,i+1);//递归
            path.remove(path.size()-1);//回溯
        }
    }
    public List<List<Integer>> findSubsequences(int[] nums) {
        backTracking(nums,0);
        return result;
    }
}