公钥密码体制

公钥密码体制的基本概念

保密性：确保信息只被授权的人访问
认证：确认某实体/数据源的真实性

保密性需要考虑到

• 不可否认性
• 数据完整性

保密系统要考虑

1. 达到实际上不可破

• 接获密文、某些明文密文对，决定密钥或者明文是不可行的

2. Kerckhoff原则 保密性不依赖于加密体制或算法的保密，而是密钥

3. 加密和解密算法适用于所有密钥空间中的元素

4. 便于实现、使用方便

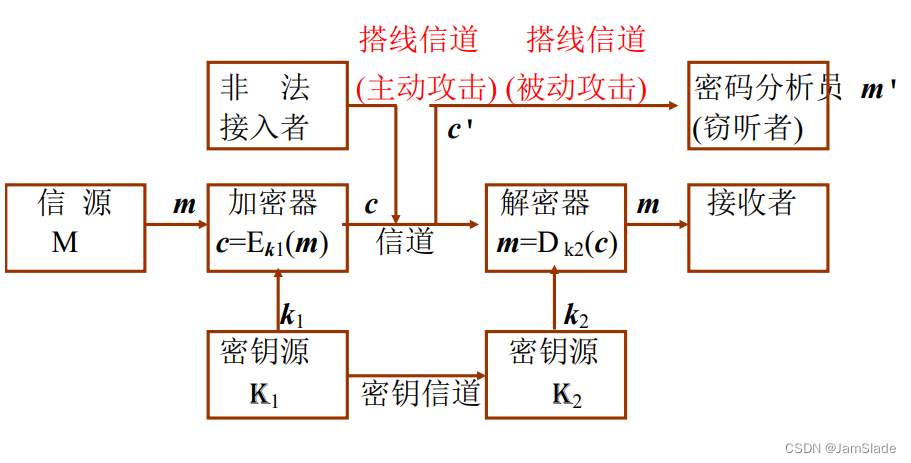
保密系统模型

$$(M,C,K_1,K_2,E_{k1},D_{k2})$$

1. 明文消息空间$M$
2. 密文消息空间$C$
3. 密钥空间$K1$和$K2$：在单钥体制下$K1=K2=K$，此时密钥 $k\in K$ 需经安全的密钥信道由发方传给收方
4. 加密变换： $E_{k1}\in E，m\to c=E_{k1}(m)$，其中$k_1\in K_1，m\in M,c\in C$ 由加密器完成。
5. 解密变换：$D_{k2}\in D，c\to m=D_{k2}(c)$，其中$k_2\in K_2，m\in M,c\in C$, 由解密器实现。

密码体制分类

单钥加密

• 流密码 STREAM CIPHER
• 分组密码 BLOCK CIPHER

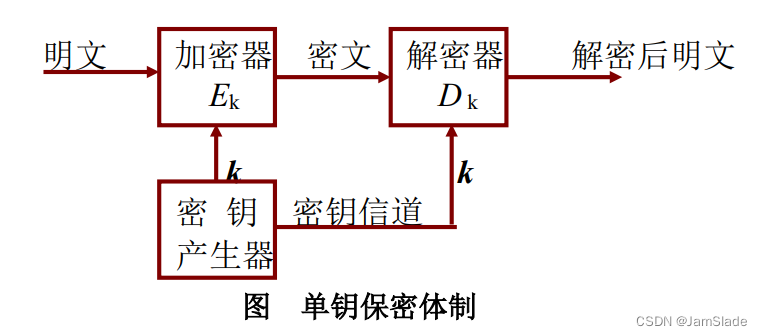
双钥加密体制
$$m=D_{kB2}(c)=D_{kB2}(E_{kB1}(m))$$

公开密钥$k_{B1}$与密文$c$推出明文$m$与密钥$k_{B2}$是不可行的

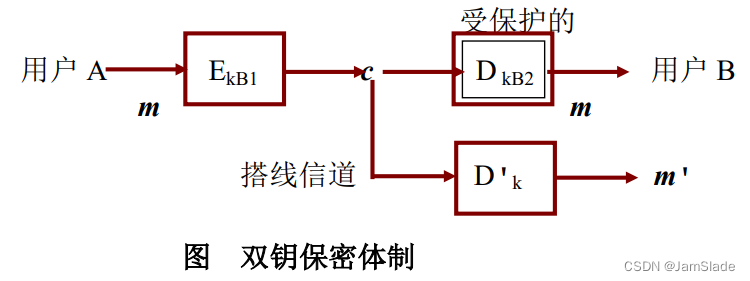
双钥认证体制

Alice吧自己密钥$k_{A2}$对消息m进行$A$的专用变换$D_{kA2}$.A 计算密文$c=D_{kA2}(m)$给用户B。B验证$m=E_{KA1}(c)=E_{kA1}(D_{kA2}(m))$是否成立

$kA2$保密，无法伪造密文$c$,所以可以认证A的身份

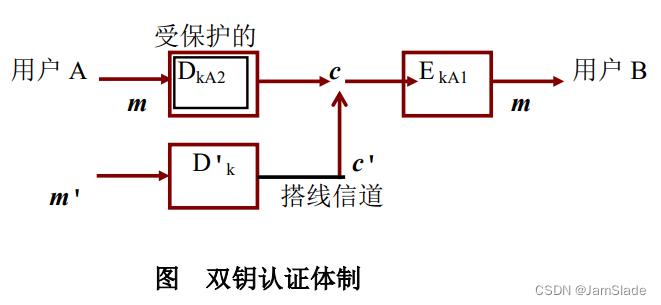
	对称密码	公钥密码
一般要求	相同密钥 共享密钥	加密解密算法相同 密钥不同 发送方有加密or解密密钥，接收方有另一个密钥
安全要求	密钥保密 无密钥无法解密 知道算法和密文无法确定密钥	保密其中一个密钥 无密钥无法解密 知道算法、密文、其中一个密钥无法确定另一个密钥
思路	简单相互推导出密钥	$K_e$公钥无法推断$K_d$私钥

理论上可以推断，实际上计算量太大，难以实施

构造公钥算法的考虑

1. 对称算法： 混乱与替换
2. 数学特性：公钥可推导私钥，但难以实现
3. 单向函数

公钥密码学

基础

单向函数

定义 1. f是A集合到B集合的映射$f:A\to B$,并且是单射，1-1映射或可逆函数

定义 2：可逆函数 $f:A\to B$ 若满足

1. $\forall x,x\in A$
2. $几乎所有x\in A$,难以由$f(x)$求出$x$

定义 3： 陷门单向函数是一类满足下述条件的单向函数

$$f_z:A_z\to B_z,z\in Z$$

Z是陷门信息集合
对所有的$z\in Z$ 给定z容易找到一对算法$E_z,D_z$,有如下性质

$$\begin{gathered} f_z(x)=E_z(x) \\ {D}_z(f_z(x))=x \end{gathered}$$
并且$\forall z\in Z$ 给定$E_z和D_z$ 对所有$x\in A$很难从$f_z(x)$算出x

单向函数

1. 多项式球根
2. Discrete Logarithm
3. Factorization Problem
4. Knapsack problem
5. Diffie-Hellman
6. Quadratic Residue
7. SQROOT

公钥、密钥体制密钥管理

1. 公钥可公开，只需要保留私钥
2. 发送方可以用人人皆知的接受方公开密钥对发送的信息进行加密，安全的传送给该接受方，然后由接受方用自己的私有密钥进行解密

公钥分发
公钥加密
数字签名

安全性：

1. 困难
2. 理论能破解，实际难破解
3. 足够长密钥 > 512bits
4. 密钥太长导致速度慢。多用于对称密钥传递

RSA公钥密码算法

密码分析者尚不能证明其安全性，但也不能否定其安全性
—— 特殊的可逆模指数运算
—— 加密/数字签名
—— 比DES慢100-1000倍

其安全性依赖于大整数分解的难度（integer fact orization problem）

参数

• $n=pq$
• $\varphi (n)=(p-1)(q-1)$
• 公钥e $(e,\varphi (n))=1$
• 私钥d $d=e^{-1}mod\varphi (n)$
• encryption $m\to c=m^{e}modn$
• decryption $c\to c^d=mmodn$

算法说明

1. q和p是两个奇素数。 $n=pq$
2. 计算n的欧拉函数$\varphi (n)=(p-1)(q-1)$
3. 选择一个整数e，e满足$1\le e<\varphi (n)\wedge (e,\varphi (n))=1$
4. 得到mod$\varphi (n)$下e的逆元 $d=e^{-1}mod\varphi (n)$
5. 公钥是n,e 密钥是d(p和q不能泄露)

$$\begin{gathered} E_{pub}(x)=x^{e}modn \\ {D}_{pri}(y)=y^{d}modn \end{gathered}$$

作用

加解密
和A不相识，B知道A的公钥也可以保密通讯。要保护公开密钥，防止修改与替换？？

数字签名、身份认证

1. A公开密钥$(e,n)$,私钥$d$,于是A对消息m签名 $s=H(m{)}^{d}modn$ 其中$H(m)$为杂凑函数(hash函数)
2. 如何验证A对m签名的有效性？ $H(m)=s^{e}modn$， 进行比对
3. 针对 篡改，伪造、抵赖（否认）、假冒
4. 对公开密钥“保护” —— 不能修改

加密和数字签名（上述两种方法）同时使用

1. A公钥 ： $(e_1,n_1)$; A私钥：$d_1$
2. B公钥 ： $(e_2,n_2)$; B私钥：$d_2$
3. A发消息m给B，签名
4. A算出 $c=((m^{e_2}mod{n}_2){)}^{d_2}mod{n}_1$
5. A发c给B
6. B验证 $m=((c^{e_1}mod{n}_1{)}^{d_2}mod{n}_2$

密钥交换

1. A和B使用堆成密钥（IDEA or DES）加密消息m
2. 用RSA交换单钥加密体制密钥
3. B产生工作密钥k，找到A的公开密钥$(e,n)$

• B 计算 $c=k^{e}modn$
• A 计算 $k=c^{d}modn$

example

p1 = 47
p2 = 71
n = 47 * 71 = 3337
\phi(n) = 46 * 70 = 3220

设置e = 79
d   = e^{-1} mod 3220
    = e^(\phi(3220) - 1) mod 3220
    = 1019

明文x = 688 232 687 966 688 3
分组
arr = [688, 232, 687, 966, 3]

for i in arr:
    i = i ^ (e) mod n;

解密 
for i in arr
    i = i ^ (d) mod n;

原理

欧拉定理
$$M^{k\varphi (n)+1}=Mmodn$$

上式中
$$n=p\times q$$
$$\varphi (n)=(p-1)(q-1)$$
$$选择e，d使得e\times d=1mod\varphi (n)$$
$$存在k使得e\times d=1+k\times \varphi (n)$$
得到
$$C^d=(M^e{)}^d=M^{1+k\varphi (n)}=Mmodn$$

安全性？

1. RSA的安全性取决于模n分解的困难性。人们完全可以设想有另外的途径破译RSA，如求解密指数d或找到(p1－1)(p2－1)等。

但这些途径都不比分解n来得容易 —— 从RSA加密的密文恢复某些bit的困难性也和恢复整组明文一样困难

2. 其他途径：从n求出$\varphi (n)$ 得到$p,q$
   $$n-\varphi (n)+1=pq-(p-1)(q-1)+1=p+q$$
   但求出它的欧拉函数等价于分解n。然而还是不知道其他方法能破解RSA且不等价于大数分解

3. 迭代攻击：
   给定
   $$(n,e,y)=(35,17,3)$$
   由于
   $$y_0=y=3$$
   计算出
   $$y_1=3^{17}=33mod35$$
   再计算
   $$y_2=y_1^{17}=33mod35$$
   对x加密多次可以再现。但当n足够大的时候，攻击方法成功概率为0

4. 选择明文
   攻击者收集用户A的密文（以密钥e加密）
   $$y=x^{e}modn$$

为了分析消息x。选择随机数
$$r<n$$
计算
$$y_1=r^{e}modn{y}_2=y_1\times ymodn$$

攻击者$A$请A对消息$y_2$进行解密得到

$$s=y_2^{d}modn$$

攻击者计算
$$\frac{s}{r}modn=x$$
得到明文$x$

(攻击者找了个明文r，用e和n把r变成y1， y1和y处理变成y2，让A解密y2得到s。s/r mod n得到明文x)

5. 共用模
   多人共用同一模数$n$, 各自选择$e,d$。 简单但不安全。 共用模秦广下，两个密钥互素，可用任意密钥恢复明文 —— 概率方法可分解n和用确定性
   算法可计算某一用户密钥而不需要分解n

6. 低加密指数攻击
   加密钥e选择得太小，则容易受到攻击

$e$选择3, 模为$n_1,n_2,n_3$ 密文如下
$$\begin{gathered} y_1=x^{3}mod{n}_{1}x<n_1 \\ {y}_2=x^{3}mod{n}_{2}x<n_2 \\ {y}_3=x^{3}mod{n}_{3}x<n_3 \end{gathered}$$
$n_1,n_2,n_3$互质，可以使用中国剩余定理，用$y_1,y_2,y_3$求出$y=x^{3}mod(n_1,n_2,n_3)$
x比三个模校，于是有$x^3<n_1{n}_2{n}_3$
$$\sqrt[3]{y}=x$$

7. 定时攻击
   测定RSA解密所进行的模指数运算的时间来估计解密指数d，而后再精确定出d 的取值

还可采用盲化技术，即先将数据进行盲化，再进行加密运算，而后做去盲运算 —— 计算时间被随机化而难于推测解密所进行的指数运算的时间

RSA参数选择

1. n

$n=p\times q$,p和q要足够大，为强素数。p 与q差要大（否则可以从n的开方入手），p-1, q-1最大公因子要小

2. e

$(e,\varphi (n))=1$条件满足，两个随机数互素概率约为$3/5$。 但e太小，x小，$y=x^{e}modn$，当$x^e<n$的时候未取模。 且容易遭受低指数攻击

3. d
   Euclidean算法在多项式时间内求出d。$d>n^{1/4}$. d小，签字和解密运算快，d不能太小，会被已知明文攻击

RSA实现中，建议用e = 3, 17, 65537这种二进制只有两位1的数据

对称算法/公钥算法

	对称	公钥
速度	快	慢
密钥管理	额外的安全信道	证书中心CA

安全性？无法简单比较

混合密码：

1. 公钥算法用于签名认证
2. 公钥算法传输密会话密钥
3. 会话密钥（对称密钥）加密数据
4. 避免密钥分配麻烦

ElGamal公钥签名算法

ElGamal,Schnorr和DSA都是基于离散对数问题的三个例子

一个既可用于数字签名又可用于加密的密码体制。

安全性依赖于 离散对数问题 discrete logarithms problem

1. 参数 $GF(n)$的本原元$g$

GF为有限域，p为素数，$GF(p)$中的加乘与普通加法区别为结果要mod p

本原元：当a模n的阶为$\varphi (n)$，当且仅当x时$\varphi (n)$使得$a^x=1modn$成立，这时候a时n的本原元

2. 秘密钥 $x\in (GF(p{)}^{\ast }-0)$
3. 公钥 $y=g^{x}modp$
4. 随机数：k

加密
$$m\to (g^k,m{y}^k)modp=(r,s)$$

解密
$$m=s{r}^{-x}modp$$

Others

1. Rabin密码
2. 背包密码
3. McEliece 体制
4. LUC密码
5. DH算法
6. 有限自动机
7. 概率加密