ACM - 数学 - 提高（还没学多少）

news2024/10/7 14:31:42

ACM - 数学 练习题

  • 一、数论
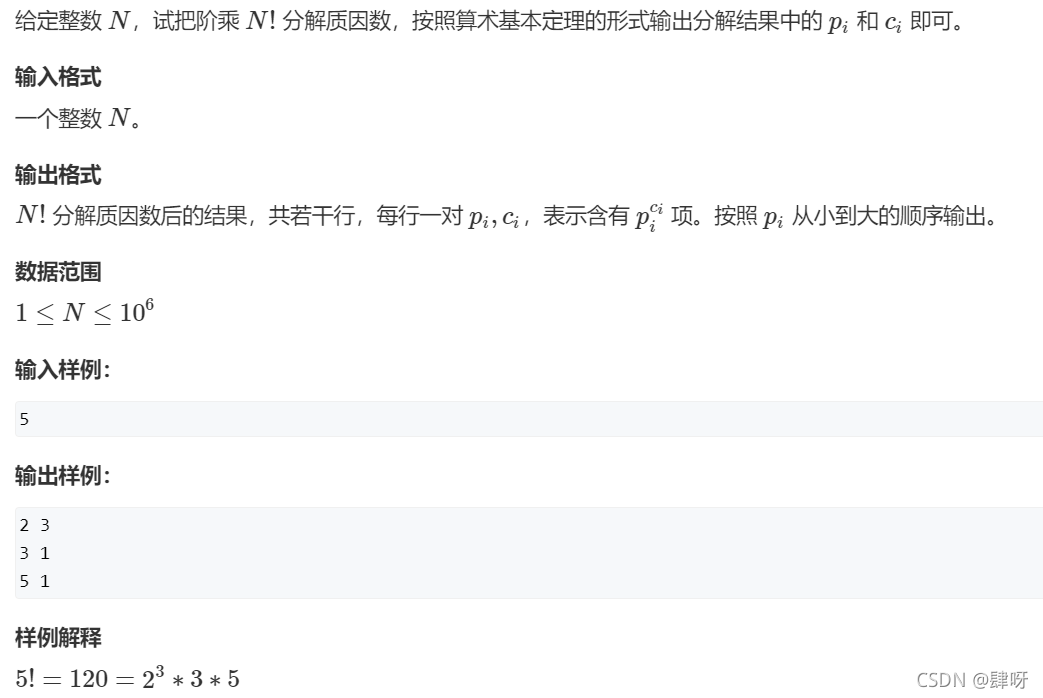
    • 1、分解质因数 ：AcWing 197. 阶乘分解
    • 2、求约数个数
      • （1）AcWing 1294. 樱花 （求 n！约数个数之和）
      • （2）AcWing 198. 反素数 （求 1 ~ N 中约数最多的数）
      • （3）AcWing 200. Hankson的趣味题（gcd * lcm == 两数之积）
    • 3、欧拉函数
      • （1）AcWing 201. 可见的点 ：求有多少组互质的点
      • （2）AcWing 220. 最大公约数 ：N内gcd为素数的数对数量
    • 4、同余
      • （1）AcWing 222. 青蛙的约会 ：求一个未知数的同余方程
      • （2）AcWing 202. 最幸运的数字：至少x个连续的8能整除L
    • 5、

一、数论

1、分解质因数 ：AcWing 197. 阶乘分解

原题链接：https://www.acwing.com/problem/content/199/
在这里插入图片描述

/*
先预处理素数，因为所有质因子只可能在素数集中。
再用 while ( n / 素数a ) 反求 n 中最多只能有多少个因子是 a。
*/
#include<iostream>

using namespace std;

const int N = 1000010;

int primes[N], cnt = 0;
bool st[N];

int ans[N];

void init() {
    int n = N - 6;
    for (int i = 2; i <= n; ++ i) {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; ++ j) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main() {
    int n;
    cin >> n;
    init();
    //统计数量
    for (int i = 0; i < cnt; ++ i) {
        int j = n;
        while (j >= primes[i]) {
            ans[primes[i]] += j / primes[i];
            j /= primes[i];
        }
    }
    //输出答案
    for (int i = 2; i <= n; ++ i) {
        if (ans[i]) printf("%d %d\n", i, ans[i]);
    }
    if (n == 1) cout << "1 1" << endl;
    return 0;
}

2、求约数个数

（1）AcWing 1294. 樱花 （求 n！约数个数之和）

原题链接：https://www.acwing.com/problem/content/description/1296/

在这里插入图片描述
思路

因为 1 / x 和 1 / y 都小于 1 / n！，所以 x 和 y 都大于 n！。
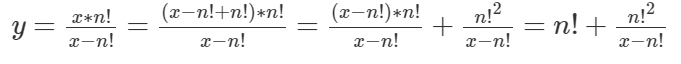
在这里插入图片描述
故而在 x 是正整数的前提下，需要（x - n!）是 n！^ 2 的约数才可行。
而每一个（x - n!）中 x 只对应一个取值，相应的 y 也有唯一的取值。
所以题目就转换成 n！^ 2 有多少个约数。

借用分解质因数的做法，先预处理素数，因为所有质因子只可能在素数集中，再用 while ( n / 素数a ) 反求 n 中最多只能有多少个因子是 a，最后记得求模求解即可。

#include<iostream>

using namespace std;

const int N = 1000010, modd = 1e9 + 7;
#define ll long long

//ans[j] 对应n！中有多少个素数j
ll ans[N], primes[N], cnt = 0;
bool st[N];

//预处理素数
void init() {
    int n = N - 6;
    for (int i = 2; i <= n; ++ i) {
        if (!st[i]) primes[cnt ++] = i;
        for (int j = 0; primes[j] <= n / i; ++ j) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) break;
        }
    }
}

int main() {
    int n;
    cin >> n;
    init();
    //求个数
    for (int i = 0; i < cnt; ++ i) {
        int j = primes[i];
        if (j > n) break;
        int m = n;
        while (m > 0) {
            ans[j] += m / j;
            ans[j] %= modd;
            m /= j;
        }
    }
    //求结果
    ll res = 1;
    for (int i = 2; i <= n; ++ i) {
        if (ans[i]) {
            res *= (ans[i] * 2 + 1);
            res %= modd;
        }
    }
    cout << res;
    return 0;
}

（2）AcWing 198. 反素数 （求 1 ~ N 中约数最多的数）

原题链接：https://www.acwing.com/problem/content/200/
在这里插入图片描述
在这里插入图片描述

/*
由约数个数定理可知，约数个数只与指数有关，N 有上限的前提下，底数越小，指数的空间才越大。
所以可以从2, 3, 5, 7, 11, 13, 17, 19, 23, 29
（不用很多素数，因为单是这些数的一次方相乘就超过2e9）去爆搜。
由于要指数之积最大，所以指数的大小应当是单调不增的，这样才越慢接近N。
*/
#include<iostream>
using namespace std;

#define ll long long

ll n, ans = 1, res = 1;
ll a[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29};
ll nums[15][40];
ll flag = 2e9;

void dfs(int idx, int cnt, ll temp, ll num) {
    if (temp > ans || (temp == ans && num < res)) {
        ans = temp;
        res = num;
    }
	for (int i = cnt; i >= 0; -- i) {
	    if (nums[idx][i] && num * nums[idx][i] <= n) {
	        dfs(idx + 1, i, temp * (i + 1), num * nums[idx][i]);
	    }
	}
}

int main () {
	cin >> n;
// 	cout << 2L * 3 * 5 * 7 * 9 * 11 * 13 * 17 * 19 * 23  << endl;
    for (int i = 0; i <= 9; ++ i) {
        for (int j = 0; j <= 31; ++ j) {
            if (j == 0) nums[i][j] = 1;
            else {
                nums[i][j] = nums[i][j - 1] * a[i];
            }
            if (nums[i][j] > flag) break;
        }
    }
	dfs(0, 30, 1, 1);
	cout << res;
}

（3）AcWing 200. Hankson的趣味题（gcd * lcm == 两数之积）

原题链接：https://www.acwing.com/problem/content/description/202/

在这里插入图片描述
在这里插入图片描述

/*
由x和a0的最大公约数是a1，并不能获得x的上限。
但是x一定是b1的约数，而b1的约数最多只有1600个。
所以可以在获得b1所有质因子和次数后，dfs枚举b1的约数，逐一判断是否合法。

或者按照下面代码的做法，获得b0的约数，假设该约数是gcd(x, b0)，
由最大公约数*最小公倍数 == x * b0获得x的取值
*/
#include<iostream>
#include<vector>
#include<cmath>
#include<unordered_map>

using namespace std;

#define ll long long

const int N = 50000;

ll n, a0, a1, b0, b1;
ll ans = 0;
int primes[N], cnt = 0;
bool st[N];

//num-质因子 cnt-该质因子出现的次数
struct node{
	ll num, cnt;
};

//初始化素数表
void init() {
	ll m = 50000;
	for (int i = 2; i <= m; ++ i) {
		if (!st[i]) primes[cnt ++] = i;
		for (int j = 0; primes[j] <= m / i; ++ j) {
			st[primes[j] * i] = true;
			if (i % primes[j] == 0) break;
		}
	}
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a % b);
}

//爆搜获得约数
void dfs(vector<node> v, int idx, ll num, unordered_map<ll, bool> book) {
	if (idx == v.size()) {
	    ll x = num * b1 / b0;
		if (book.find(x) == book.end() && gcd(x, a0) == a1 && gcd(x, b0) == num && x * b0 == b1 * num) {
		     ++ ans;
		     book[x] = true;
		}
		return;
	}
	for (int i = 0; i <= v[idx].cnt; ++ i) {
		dfs(v, idx + 1, num * pow(v[idx].num, i), book);
	}
}

void solve() {
	vector<node> nums;
	unordered_map<ll, bool> book;
	ll b = b0;
	//获得质因子和次数
	for (int i = 0; i < cnt; ++ i) {
		ll c = 0;
		while (b % primes[i] == 0) {
			++ c;
			b /= primes[i];
		}
		if(c > 0) {
		    nums.push_back({primes[i], c});
		}
	}
	if (b > 1) nums.push_back({b, 1});
	dfs(nums, 0, 1, book);
}


int main () {
	cin >> n;
	init();
	while (n --) {
		cin >> a0 >> a1 >> b0 >> b1;
		ans = 0;
		solve();
		cout << ans << endl;
	}
}

3、欧拉函数

（1）AcWing 201. 可见的点 ：求有多少组互质的点

原题链接：https://www.acwing.com/problem/content/203/
在这里插入图片描述
在这里插入图片描述

/*
本题抽象出来就是找所有第一象限过原点且斜率不同的直线有多少条。
设直线穿过点 x0、y0，由 y = kx 可得 k = y0 / x0。
假如 x0 和 y0 不互质，设他们存在大于 1 的公因数 d，那么点（x0 / d， y0 / d）也穿过该直线。
故而本题其实就是求解有多少组不同的（x，y）互质 ==》欧拉函数
*/
#include<iostream>

using namespace std;

const int N = 1010;

int primes[N], cnt = 0;
int e[N];
bool st[N];

void init() {
    int n = N - 5;
    e[1] = 1;
    for (int i = 2; i <= n; ++ i) {
        if (!st[i]) {
            primes[cnt ++] = i;
            e[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; ++ j) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) {
                e[primes[j] * i] = primes[j] * e[i];
                break;
            }
            e[primes[j] * i] = e[i] * (primes[j] - 1);
        }
    }
}

int main() {
    int t;
    cin >> t;
    init();
    for (int i = 1; i <= t; ++ i) {
        int n;
        cin >> n;
        int ans = 1;  
        for (int j = 1; j <= n; ++ j) ans += e[j] * 2; // 关于 y = x 对称
        cout << i << " " << n << " " << ans << endl;
    }
}

（2）AcWing 220. 最大公约数 ：N内gcd为素数的数对数量

原题链接：https://www.acwing.com/problem/content/222/
在这里插入图片描述

/*
假设gcd(x, y) = d (d是素数)，那么显然 gcd(x/d, y/d) = 1。
这意味着 x/d 和 y/d 是互质的。
据此，我们可以枚举 n 内的素数，求 n/d 范围所有能互质的对子的总数量。
受上一题（AcWing 201. 可见的点）的启发，我们可以预设 x/d <= y/d，先求对角线的一半，再翻倍即可。
res += 2 * sum[n / p] - 1; 是因为在乘2运算的时候对角线上的e[1]会被算两次，所以需要减1。
*/

#include<iostream>

using namespace std;

const int N = 10000010;
#define ll long long

int n;
int e[N],primes[N], cnt = 0;
bool st[N];
ll sum[N];  //欧拉函数的前缀和


void init() {
    e[1] = 1;
    for (int i = 2; i <= n; ++ i) {
        if (!st[i]) {
            primes[cnt ++] = i;
            e[i] = i - 1;
        }
        for (int j = 0; primes[j] <= n / i; ++ j) {
            st[primes[j] * i] = true;
            if (i % primes[j] == 0) {
                e[primes[j] * i] = primes[j] * e[i];
                break;
            }
            e[primes[j] * i] = e[i] * (primes[j] - 1);
        }
    }
    for (int i = 1; i <= n; ++ i) sum[i] = sum[i - 1] + e[i];
}

int main() {
    cin >> n;
    init();
    ll res = 0;
    for (int i = 0; i < cnt; ++ i) {
        int p = primes[i];
        res += 2 * sum[n / p] - 1;
    }
    cout << res;
    return 0;
}

4、同余

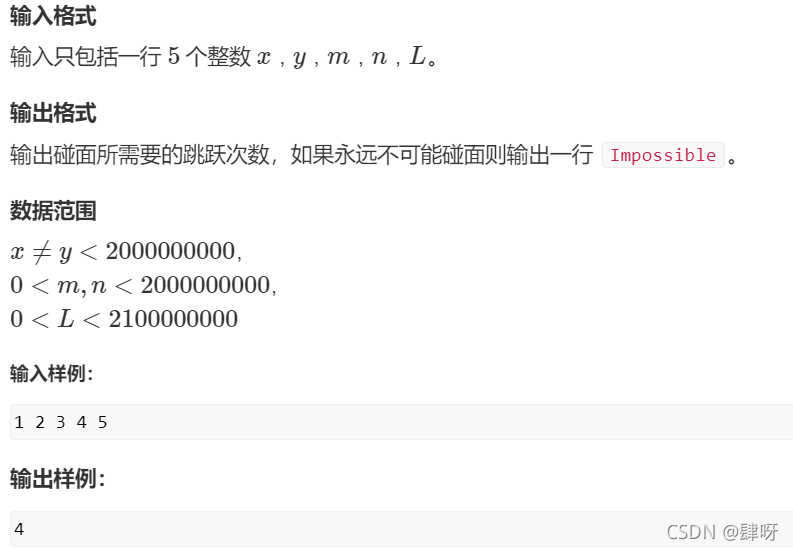
（1）AcWing 222. 青蛙的约会 ：求一个未知数的同余方程

原题链接：https://www.acwing.com/problem/content/224/
在这里插入图片描述
在这里插入图片描述

/*
假设青蛙跳了 p 次，一共走了 q 个整圈，那么 p * (m - n) - q * l = y - x。
由于只有p、q是未知数，所以直接用exgcd求即可。
注意 d | (y - x) 才有解，而且最终跳的次数 p 需要乘上 (y - x) / d 才是方程的一组解。
最后再对 l / gcd 取模求最小整数解即可ac。
*/
#include<iostream>

using namespace std;

#define ll long long

ll exgcd(ll a, ll b, ll &x, ll &y) {
    if (b == 0) {
        x = 1;
        y = 0;
        return a;
    }
    ll d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main() {
    ll x, y, m, n, l, a, b;
    cin >> x >> y >> m >> n >> l;
    ll d = exgcd(m - n, l, a, b);
    if ((y - x) % d == 0) {
        a *= ((y - x) / d);
        ll u = abs(l / d);   //注意求绝对值
        cout << (a % u + u) % u << endl;
    }
    else cout << "Impossible";
    return 0;
}

（2）AcWing 202. 最幸运的数字：至少x个连续的8能整除L

原题链接：https://www.acwing.com/problem/content/description/204/
在这里插入图片描述
在这里插入图片描述

思路
在这里插入图片描述
① 使用欧拉定理时，10 和 c 互质的证明
把同余方程写成 10 ^ x + p * c = 1 的形式（p为未知数），假如 10 和 c 不互质，那么至少可以对等式左边提取出一个公因子 d，即： d * （10 ^ x / d + p * c / d）= 1.
很明显括号内的值不为0，当把 d 移到等式右边时，1 / d 不能整除且不能和左边相等，故而 d 必然为 1，即 10 和 c 一定互质。

② 同余方程的乘法法则
假如 a 同余 b（mod c），x 同余 y（mod c），那么 a * x 同余 b * y （mod c）。

= = = = =》

综上，我们可以发现先求出常数 c = 9 * L / gcd(L, 8)，再求和 c 互质的数的个数 phi，再用快速幂check一遍phi的除数中能满足同余方程的最小的除数。

当然快速幂过程有10次方 * 10次方，所以需要在乘法过程中用一下龟速乘。

代码

//推导过程太过摧枯拉朽
#include<iostream>
#include<cmath>

using namespace std;

#define ll long long

ll l, phi, c;

//求a和b的最大公约数
ll gcd(ll a, ll b) {
    return b ? gcd(b, a % b) : a;
}

//求1~c中有多少个和c互质的数
ll eul(ll c) {
    ll res = c;
    ll len = sqrt(c);
    for (ll i = 2; i <= len; ++ i) {
        if (c % i == 0) {
            while (c % i == 0) {
                c /= i;
            }
            res /= i;
            res *= (i - 1);
        }
    }
    if (c != 1) {
        res /= c;
        res *= (c - 1);
    }
    return res;
}

//龟速乘：求（a * b）% p
ll qmul(ll a, ll b, ll p) {
    ll res = 0, t = a;
    while (b) {
        if (b & 1) res = (res + t) % p;
        b >>= 1;
        t = (t + t) % p;
    }
    return res;
}

//快速幂：求10的k次方mod c
ll qmi(ll a, ll k, ll p) {
    ll res = 1, t = a;
    while (k) {
        if (k & 1) res = qmul(res, t, p);
        k >>= 1;
        t = qmul(t, t, p);
    }
    return res == 1;
}

//check(k)：判断10的k次方模c是不是等于1，即判断k是不是一组解
bool check(ll k) {
    return qmi(10, k, c) == 1;
}

int main() {
    int k = 1;
    while (cin >> l, l) {
        ll ans = 0x3f3f3f3f3f;
        c = 9 * l / gcd(l, 8);
        if (c % 2 == 0 || c % 5 == 0) ans = 0;
        phi = eul(c);
        
        for (ll i = 1; i <= phi / i; ++ i) {
            if (phi % i == 0) {
                if (check(i)) ans = min(ans, i);
                if (check(phi / i)) ans = min(ans, phi / i);
            }
        }
        printf("Case %d: %lld\n", k, ans);
        ++ k;
    }
    return 0;
}

5、

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/509588.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

human-NeRF 代码运行环境完全打包（根据照片视频生成三维模型）

human-NeRF 代码运行环境完全打包（根据照片视频生成三维模型）

包含模型和可以直接运行的数据的代码环境&#xff08;window环境&#xff0c;linux应该也可以运行&#xff09;&#xff0c;下载链接放在文章最后&#xff0c;不需要你自己再去下载任何的代码和模型了。 下载后输入三行命令在命令行界面即可将代码跑起来&#xff1a; pip insta…
阅读更多...
C++14:AVL树

C++14:AVL树

由于二叉搜索树在某些特定的情况下会退化成单叉树,为了解决这个问题&#xff0c;保证二叉搜索树能在绝大多数情况下保持高速搜索&#xff0c;G.M. Adelson-Velsky和E.M. Landis这两位俄国数学家提出了AVL树的概念&#xff0c;也就是高度平衡的搜索二叉树。 AVL树平衡大体逻辑&…
阅读更多...
ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）

ACM - 数据结构 - 基础（数组模拟链表 / 栈 / 队列 + 字典树 + 并查集 + 堆 + 哈希）

数据结构 一、线性表1、单链表模板题&#xff1a;AcWing 826. 单链表 2、双链表模板题 AcWing 827. 双链表 3、栈数组模拟栈模板 AcWing 828. 模拟栈逆波兰简版模板例题1、逆波兰表达式&#xff1a;HDU 1237 简单计算器&#xff08;写得有点复杂&#xff09; 4、队列数组模拟队…
阅读更多...
接口自动化测试可以使用的几个常用的框架

接口自动化测试可以使用的几个常用的框架

接口自动化测试可以使用以下几个常用的框架&#xff1a; 1、pytest pytest是一个用于Python编写单元测试和功能测试的框架。它提供了简洁的语法、灵活的扩展性和丰富的插件&#xff0c;可以帮助开发人员高效地编写测试用例&#xff0c;并快速定位和解决问题。 以下是pytest的…
阅读更多...
数据结构刷题（三十一）：1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II

数据结构刷题（三十一）：1049. 最后一块石头的重量 II、完全背包理论、518零钱兑换II

一、1049. 最后一块石头的重量 II 1.思路&#xff1a;01背包问题&#xff0c;其中dp[j]表示容量为j的背包&#xff0c;最多可以背最大重量为dp[j]。 2.注意&#xff1a;递推公式dp[j] max(dp[j], dp[j - stones[i]] stones[i]);本题中的重量就是价值&#xff0c;所以第二个…
阅读更多...
边缘计算盒子适合用于哪些场景？

边缘计算盒子适合用于哪些场景？

边缘计算盒子适用于在智慧工地、智慧工厂、智慧园区和智慧城管等场景中可以实现多种算法功能&#xff0c;以下是一些应用和实现算法功能&#xff1a; 智慧工地&#xff1a;实时视频监控与分析&#xff1a;边缘计算盒子可以处理实时监控视频流&#xff0c;进行人员和车辆识别、…
阅读更多...
OpenPCDet系列 | 5.PointPillars模型前向传播完整流程

OpenPCDet系列 | 5.PointPillars模型前向传播完整流程

文章目录 前向传播流程1. 模型初始化2. 模型训练前向传播前向传播流程 这里以PointPillars模型为例，在PointPillars模型中主要划分了以下4个主要的模块，以下某块首先会在build_network中进行初始化，然后在具体前向传播时通过forward函数进行。下面进行区分。 PointPillars…
阅读更多...
新颖拓扑指纹助力虚拟筛选：ToDD革新计算机辅助药物发现之路

新颖拓扑指纹助力虚拟筛选：ToDD革新计算机辅助药物发现之路

编译 | 于洲 今天我们介绍由Novartis集团的Novartis与德克萨斯大学达拉斯分校的Baris Coskunuzer为第一作者发表在NeurIPS 2022会议上的工作&#xff0c;文章介绍了一种新的虚拟筛选方法——ToDD模型&#xff0c;该方法使用了多参数持久性同调&#xff08;MP&#xff09;来生成…
阅读更多...
wx.request get请求重定向问题

wx.request get请求重定向问题

微信小程序wx.request请求&#xff0c;重定向问题。 背景 在开发微信小程序项目的时候&#xff0c;使用wx.request请求一个公共接口&#xff0c;结果请求被重定向多次之后&#xff0c;返回失败&#xff0c;而且没有 code 码&#xff0c;只有一个 errMsg: request:fail。 Netw…
阅读更多...
OpenShift - 使用 Ansible Automation Platform 纳管 OpenShift Virtualization 虚机

OpenShift - 使用 Ansible Automation Platform 纳管 OpenShift Virtualization 虚机

《OpenShift / RHEL / DevSecOps 汇总目录》 说明&#xff1a;本文已经在支持 OpenShift 4.12 的 OpenShift 环境中验证 本文所用到的运行环境和配置方法请先参照以下 blog 准备&#xff1a; 《OpenShift 4 - 安装部署 Ansible Automation Platform 4.x 控制台》《OpenShift …
阅读更多...
React 组件

React 组件

文章目录 React 组件复合组件 React 组件 本节将讨论如何使用组件使得我们的应用更容易来管理。 接下来我们封装一个输出 “Hello World&#xff01;” 的组件&#xff0c;组件名为 HelloMessage&#xff1a; React 实例 <!DOCTYPE html> <html> <head> &…
阅读更多...
css中的grid高频布局

css中的grid高频布局

1.需求 1.一个父级容器内有n个子元素; 2.每个子元素最小宽度是100px&#xff1b; 3.每个子元素最大宽度根据屏幕宽度自适应&#xff1b; 4.每个子元素的宽度保持同宽&#xff1b; 5.每个元素之间有间隔&#xff0c;每一行的两边不留间隙&#xff0c;每一列的上下不留间隙&…
阅读更多...
2.V853支持WIFI和有线网卡

2.V853支持WIFI和有线网卡

100ASK-V853-PRO开发板支持WIFI和有线网卡 0.前言 ​ 通过上一章节&#xff0c;我们已经成功下载Tina SDK包&#xff0c;完成编译并烧写Tina Linux系统&#xff0c;接下来展示100ASK_V853-PRO开发部如何通过WIFI和有线网卡进行上网。 全志Linux Tina-SDK开发完全手册&#x…
阅读更多...
02-mysql升级篇（rpm方式+压缩包升级）

02-mysql升级篇（rpm方式+压缩包升级）

文章目录 升级方式一、二进制方式安装1、下载mysql-5.7.42安装包&#xff08;mysql-5.7.37升级mysql-5.7.42&#xff09;2、备份数据库、my.cnf文件&#xff0c;停止mysql服务&#xff08;重要&#xff09;3、查看当前数据库版本3、上传 mysql-5.7.42-1.el7.x86_64.rpm-bundle.…
阅读更多...
SpringMVC 详解

SpringMVC 详解

文章目录 一、SpringMVC简介1、什么是MVC2、什么是SpringMVC3、SpringMVC的特点 二、HelloWorld1、开发环境2、创建maven工程a>添加web模块b>打包方式&#xff1a;warc>引入依赖 3、配置web.xmla>默认配置方式b>扩展配置方式 4、创建请求控制器5、创建springMVC…
阅读更多...
关于太阳黑子数的查询

关于太阳黑子数的查询

太阳黑子数查询地址&#xff1a;点此跳转 浏览器中打开下图所示的网站。 根据自己的需求下载相应的文件查找太阳黑子数&#xff0c;下载时可以选择 TXT 文件格式&#xff0c;也可以选择 CSV 文件格式。 我下载了每日估计的太阳黑子数&#xff0c;TXT 格式文件打开如下图所示。…
阅读更多...
免费下载的无水印人物素材网站！

免费下载的无水印人物素材网站！

在日常设计中&#xff0c;设计师常常需要使用人物素材来提升设计作品的吸引力。一个可爱的人物插画可以使网页界面更加生动&#xff0c;一个富有个性的人物素材可以让应用程序更具吸引力&#xff0c;引发用户的共鸣。但设计师有时会苦恼于找不到合适的人物素材网站&#xff0c;…
阅读更多...
PCB制板基础知识[详细版]

PCB制板基础知识[详细版]

一、PCB概念 PCB&#xff08;PrintedCircuitBoard&#xff09;&#xff0c;中文名称为印制电路板&#xff0c;又称印刷电路板、印刷线路板&#xff0c;是重要的电子部件&#xff0c;是电子元器件的支撑体&#xff0c;是电子元器件电气连接的提供者。由于它是采用电子印刷术制…
阅读更多...
USB descriptor

USB descriptor

如下为oneplus的插入MIDI模式 device descriptor 注意&#xff1a;1个device只有一个描述符 bNumConfigurations 标识只有一个配置&#xff0c;该配置只属于一个传输速度 通过getDescriptor的方法获得&#xff0c;需要指定wvalue为deivce descriptor,至于index可以为0 大概1…
阅读更多...
【5.JS基础-JavaScript的DOM操作】

【5.JS基础-JavaScript的DOM操作】

1 认识DOM和BOM 所以我们学习DOM&#xff0c;就是在学习如何通过JavaScript对文档进行操作的&#xff1b; DOM Tree的理解 DOM的学习顺序 DOM的继承关系图 2 document对象 3 节点&#xff08;Node&#xff09;之间的导航&#xff08;navigator&#xff09; 4 元素&#xff0…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023