预备知识：

论文笔记

1. Introduction

2. Elastic weight consolidation

2.1 EWC allows continual learning in a supervised learning context

2.2 EWC allows continual learning in a reinforcement learning context

3. Conclusion

文章链接：https://arxiv.org/abs/1612.00796

预备知识：

有关Life-Long Learning：Lecture 14：Life-long Learning_zzz_qing的博客-CSDN博客

Life-Long Learning Goal: A model can beat all task!

Life-Long Learning有很多种不同的做法，EWC属于Regularization-based methods：

在李宏毅老师Life-Long Learning课程对应的HW14中，给出了EWC的简介和相关代码：

The ewc class applied EWC algorithm to calculate the regularization term. Here we will focus on the algorithm of EWC.

In this assignment, we want to let our model learn 10 tasks successively. Here we show a simple example that lets the model learn 2 tasks(task A and task B) successively.

In the EWC algorithm, the definition of the loss function is shown below:

Assume we have a neural network with more than two parameters.

下面是EWC的部分代码，由代码可知道EWC需要使用label数据：

# Simply use groud truth label of dataset.  
label = data[1].to(self.device)
          
# generate Fisher(F) matrix for EWC     
loss = F.nll_loss(F.log_softmax(output, dim=1), label)
loss.backward()   

for n, p in self.model.named_parameters():
  # get the gradient of each parameter and square it, then average it in all validation set.                          
  precision_matrices[n].data += p.grad.data ** 2 / number_data

def penalty(self, model: nn.Module):
  loss = 0
  for n, p in model.named_parameters():
    # generate the final regularization term by the ewc weight (self._precision_matrices[n]) and the square of weight difference ((p - self.p_old[n]) ** 2).  
    _loss = self._precision_matrices[n] * (p - self.p_old[n]) ** 2
    loss += _loss.sum()
  return loss

论文笔记

本文通过选择性地放慢对那些任务重要的权重的学习来记住旧任务。

本文通过解决一组基于 MNIST 手写数字数据集的分类任务并通过顺序学习多个 Atari 2600 游戏来证明我们的方法是可扩展且有效的。

1. Introduction

intelligent agents必须展示持续学习的能力：即学习连续任务而不忘记如何执行先前训练的任务的能力。

关于灾难性遗忘相关知识点在life-long learning笔记中有，这里不赘述。

在life-long learning笔记中有提到同时训练多个任务不会发生灾难性遗忘，本文给出了解释：在实现continual learning方面，当前的方法通常确保来自所有任务的数据在训练期间同时可用。通过在学习期间交错来自多个任务的数据，不会发生遗忘，因为网络的权重可以针对所有任务的性能进行联合优化。在这种机制中——通常被称为多任务学习范式——深度学习技术已被用于训练能够成功玩多个 Atari 游戏的单个智能体。（在这篇文献提出的时间点，按顺序学习任务就是把所有任务的数据都记下来，学习新任务的时候再把前面的任务再学一遍，需要存储很多数据，训练起来也很慢）

本研究为人工神经网络开发了一种弹性权重整合（简称 EWC）算法。该算法根据某些权重对先前看到的任务的重要性来减慢对某些权重的学习。我们展示了 EWC 如何用于监督学习和强化学习问题以按顺序训练多个任务而不忘记旧任务。

2. Elastic weight consolidation

在本节中，我们将解释为什么我们希望在旧任务的邻域中找到新任务的解决方案，我们如何实现约束，最后我们如何确定哪些参数是重要的。

深度神经网络由多层linear projection followed by element-wise non-linearities组成。学习任务包括调整linear projection的一组权重和偏差 θ，以优化性能。 θ 的许多配置将导致相同的性能，这与 EWC 相关：过度参数化使得任务 B 的解决方案 θ* B 很可能与之前找到的任务 A 的解决方案 θ* A 很接近。因此，在学习任务 B 时，EWC 保护了通过将参数限制在以 θ* A 为中心的任务 A 的低误差区域中，可以提高任务 A 的性能，如图 1 中的示意图所示：（这就是李宏毅老师在Regularization-based的方法中介绍的思想）

为了证明这种约束选择的合理性并定义哪些权重对任务最重要，从概率的角度考虑神经网络训练是很有用的。从这个角度来看，优化参数无异于在给定一些数据 D 的情况下找到它们最可能的值。我们可以根据参数 p(θ) 的先验概率和数据 p(D|θ) 使用贝叶斯规则：

关于任务 A 的所有信息都必须被吸收到后验分布 p(θ|DA) 中。这个后验概率必须包含关于哪些参数对任务 A 很重要的信息，因此是实施 EWC 的关键。

真正的后验概率是难以处理的，因此将后验近似为高斯分布，其均值由参数 θ∗ A 给出，对角线精度由 Fisher 信息矩阵 F 的对角线给出。F 具有三个关键属性：(a) 它相当于接近最小值的损失的二阶导数，(b) 它可以单独从一阶导数计算，因此即使计算也很容易对于大型模型，(c) 它保证是半正定的。

这种方法类似于期望传播，其中每个子任务都被视为后验的一个因素。给定这个近似值，我们在 EWC 中最小化的函数 L 是：

LB(θ) 仅是任务 B 的损失，λ 设置旧任务与新任务相比的重要性，i 标记每个参数。

2.1 EWC allows continual learning in a supervised learning context

如图 A 所示，使用普通随机梯度下降 (SGD) 对这一系列任务进行训练会导致灾难性遗忘。

这个问题不能通过对每个权重使用固定的二次约束（绿色曲线，L2 正则化）对网络进行正则化来解决。对每个权重使用固定的二次约束会导致任务 A 中的性能下降要轻得多，但任务 B 无法正确学习，因为约束保护了所有权重，导致在 B 上留下很少的剩余容量来学习。但是，当我们使用 EWC 时，考虑到了每个权重对任务 A 的不同的重要性，网络可以很好地学习任务 B 而不会忘记任务 A（红色曲线）。

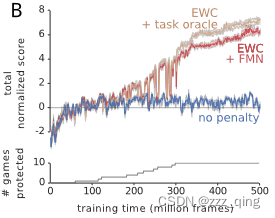
将传统的 dropout 正则化与 EWC 进行比较，单独使用 dropout 正则化的随机梯度下降是有限的，并且它不能扩展到更多任务（图 B）。相比之下，EWC 允许按顺序学习大量任务，错误率只会适度增长：

EWC 允许网络有效地将更多功能压缩到具有固定容量的网络中。下面评估它是否为每个任务分配完全独立的网络部分，或者是否通过共享表示以更有效的方式使用容量（通过测量任务对各自的 Fisher 信息矩阵之间的重叠来确定每个任务是否依赖于相同的权重集，小的重叠意味着这两个任务依赖于不同的权重集，大的重叠表明两个任务都使用了权重）。

图 C 显示了作为深度函数的重叠。作为一个简单的控制，当一个网络在两个非常相似的任务上进行训练时，这些任务依赖于整个网络中相似的权重集（灰色曲线） .当这两个任务彼此更加不同时，网络开始为这两个任务（黑线）分配单独的容量（即权重）。然而，即使对于大排列，更靠近输出的网络层确实被重新用于两个任务。这反映了这样一个事实，即排列使输入域非常不同，但输出域（即类标签）是共享的。

2.2 EWC allows continual learning in a reinforcement learning context

为了在RL中应用 EWC，在每个任务切换时计算 Fisher 信息矩阵。对于每个任务，都会添加一个惩罚，其中锚点由参数的当前值给出，权重由 Fisher 信息矩阵乘以通过超参数搜索优化的缩放因子 λ 给出。我们只对经历了至少 2000 万帧的游戏添加了 EWC 惩罚。

我们还允许 DQN 代理为每个推断的任务维护单独的短期记忆缓冲区：这些允许使用经验重放机制在策略外学习每个任务的动作值。因此，整个系统在两个时间尺度上有记忆：在短时间尺度上，经验回放机制允许 DQN 中的学习基于交错和不相关的经验。在更长的时间范围内，跨任务的专业知识通过使用 EWC 得到整合。最后，我们允许少量网络参数特定于游戏，而不是跨游戏共享。特别是，我们允许网络的每一层都有特定于每个游戏的偏差和每个元素的乘法增益。

实验结果表明，通过使用 EWC，agent确实学会了玩多个游戏：