前言

断断续续，终于完成了这本书的第一次通读，记录下自己的一些想法。

先说一个小故事。前段时间家里买了一个小鱼缸，问我有没有办法让水自动循环，但不想用电。没有好的想法，去小某书上搜了下，好多案例教程。其中一个是借助于一些简单的工具（矿泉水瓶、导管），实现水的自动循环，效果如下图所示。思考了下，剔除了这个方案。没有外部能量的注入，将水从低处帮运到高处，违背物理常识（超出了这些工具的能力边界）。
在这里插入图片描述

正文

言归正传，《计算之魂》这本书，给我印象最深的一个点，是识别能力边界。书中讲了一个“12球问题”的案例，内容如下：有12个球外观一模一样，其中一球为假，所有真球重量一样，假球重量不同。现有一个天枰，只称3次，如何找出假球并判断其重量比真球小还是大？我自己思考许久未得齐法，作者（吴军老师）解答时讲了一个很重要的观点，先识别他是否有解。12个球，均有轻和重两种选择，共24种可能性；天平一次称重，可能有三种结果，3次称重，共有27种可能性，27>24，故此问题有解。无独有偶，近期工作中也遇到了类似的问题，基于这个思路，识别出问题已经超出了能力边界，减少了资源的无效投入。

其次，计算机思维的认知。递归、分治，是很重要的计算机思维。将大问题（逐步）转换为小问题，基于既定的规则做大量重复工作，是计算机所擅长的。以汉诺塔游戏为例，可以看到递归的美。
汉诺游戏规则如下：有三根相邻的柱子，标号为A、B、C；A柱子从下到上按金字塔状叠放着n个不同大小的圆盘；现在需要把所有盘子从A经由B移动到C，一次只能移动一个盘子且同一根柱子上都不能出现大盘子在小盘子上方，写出伪代码实现。
在这里插入图片描述

    递归伪代码实现如下：

function hanoi(起始柱source, 目标柱target, 帮助柱help, 盘子数量N) {
    // 将前N-1个盘子，从A经过C移到B
   hanoi（source, help, target, N-1)；
    // 将第N个盘子，从A移到C
   move 第N个盘，从source移到target；
    // 将前N-1个盘子，从B经过A移到C
   hanoi（help, target, source, N-1)；
}

hanoi(A, C, B, n);

递归，实现很简洁，不使用递归，其复杂度可想而知。

第三点，是作者通过一些简单的例子，将计算机的认知讲解的很透彻。
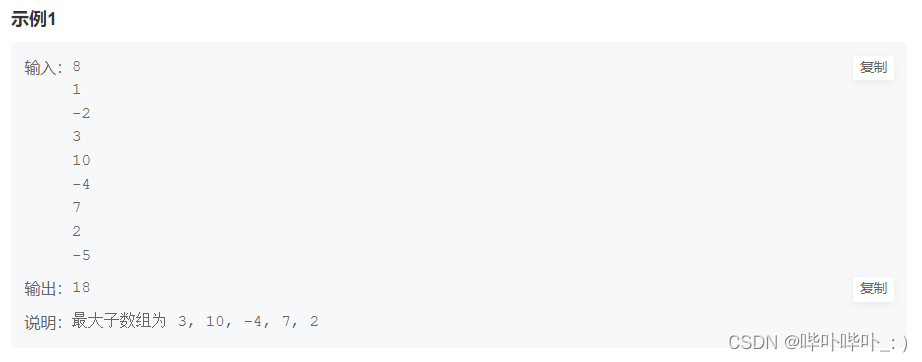
以计算机二进制信息编码为例，通过小白鼠试验进行讲解。有100瓶药水，其中一瓶有毒。用小白鼠来试药，喝到有毒的药，一天后会死掉，喝无毒（包括同时喝几种，各种药不会产生综合效应）的正常。现在只有一天时间需要找出毒药，一只小白鼠只能参与一次实验，请问需要多少只小白鼠。
简化问题，以8瓶药来说明，给药进行编号，对应0-7，其对应的二进制信息为3个bit。每只小白鼠吃药后只有两种结果：正常或死亡，即可以表示1个bit的信息，故需要3只小白鼠。
下表为分析过程，每个小白鼠对应一个bit位，1表示小白鼠喝对应的药水；假设小白鼠A、C死亡，则说明编号为5的药水有毒（二进制编码101）。
在这里插入图片描述