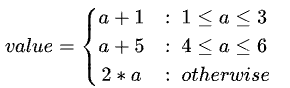1401D - Maximum Distributed Tree
求每个边经过的次数,假设求u,v这条边的次数,边的左端是u这个集合一共有n-siz[v]个点,右端是v这个集合有siz[v]个端点,经过这条边的次数就是siz[v]*(n-siz[v]),然后再按照次数多的乘以大的质因数就可以了,注意m可能大于n-1
D. Maximum Distributed Tree(贪心+树dfs)_小菜鸡加油的博客-CSDN博客
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define pause system("pause")
#define int long long
const int mod=1e9+7;
const int inf=1e18;
const int N = 4e5+100;
const double eps=1e-10;
int qpow(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int sgn(double x)
{
if(fabs(x)<eps) return 0;
else if(x<0) return -1;
else return 1;
}
int getinv(int a){return qpow(a,mod-2LL);}
int head[N],cnt;
struct Edge
{
int next,to;
}e[N];
void addedge(int from,int to)
{
e[++cnt].next=head[from];
e[cnt].to=to;
head[from]=cnt;
}
int siz[N],t,n,m,p[N],a[N],ct;
bool cmp(int a,int b){return a>b;}
void dfs(int u,int fa)
{
siz[u]=1;
for(int i=head[u];i;i=e[i].next)
{
int j=e[i].to;
if(j==fa) continue;
dfs(j,u);
siz[u]+=siz[j];
a[++ct]=siz[j]*(n-siz[j]);
}
}
signed main()
{
//ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("in.txt","r",stdin);
cin>>t;
while(t--)
{
cin>>n;
for(int i=1;i<=n;i++) siz[i]=head[i]=0;cnt=ct=0;
for(int i=1;i<n;i++)
{
int u,v;cin>>u>>v;
addedge(u,v);addedge(v,u);
}
dfs(1,0);
cin>>m;
for(int i=1;i<=m;i++) cin>>p[i];
int ans=0;
if(m<=ct)
{
sort(a+1,a+ct+1,cmp);
sort(p+1,p+m+1,cmp);
for(int i=m+1;i<=ct;i++) p[i]=1;
for(int i=1;i<=ct;i++)
{
ans=(ans+(p[i]*a[i]%mod))%mod;
//cout<<ans<<" "<<p[i]<<" "<<a[i]<<endl;
}
}
else
{
//cout<<"sss"<<endl;
sort(a+1,a+ct+1);
sort(p+1,p+m+1);
int tmp=1;
for(int i=ct+1;i<=m;i++) tmp=tmp*p[i]%mod;
p[ct]=p[ct]*tmp%mod;
for(int i=ct;i>=1;i--)
{
ans=(ans+(p[i]*a[i]%mod))%mod;
// cout<<ans<<" "<<p[i]<<" "<<a[i]<<endl;
}
}
cout<<ans<<endl;
for(int i=1;i<=max(ct,m);i++) p[i]=a[i]=0;
}
pause;
return 0;
}F. Function! 2019银川,类似整除分块
因为当b>a的时候,都是小于1的,上取整之后就是1,所以整个式子就变成
,当
时,
,所以右边的求和其实就是(n-a+1),这玩意是可以化简得,
,
一个是等差数列求和,一个是平方和,这就可以o(1)得算出来了;
然后时直接暴力算,但发现对于一个b,会有一段连续的a log值时一样的,所以可以利用类似整除分块的思想来优化一下;
2019ICPC(银川) - Function!(数论+数学分块)_Frozen_Guardian的博客-CSDN博客
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define pause system("pause")
#define int long long
const int mod=998244353;
const int inf=1e18;
const int N = 4e5+100;
const double eps=1e-10;
int qpow(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int sgn(double x)
{
if(fabs(x)<eps) return 0;
else if(x<0) return -1;
else return 1;
}
int getinv(int a){return qpow(a,mod-2LL);}
int n;
int cal(double a,double b)
{
return floor(log2(b)/log2(a));
}
signed main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("in.txt","r",stdin);
cin>>n;
int ans=0,a;
for(a=2;a*a<=n;a++)
{
int tmp=0;
int qp=a;
int x=1;
for(int b=a;b<=n;b++)
{
int d=min(n,qp*a-1LL);
tmp=(tmp+x*((d-b+1)%mod)%mod)%mod;
b=d;
qp*=a;x++;
//cout<<b<<endl;
}
ans=(ans+tmp*a%mod)%mod;
}
//cout<<ans<<endl;
a--;
int x1=((n%mod)*((n+1)%mod)%mod)*getinv(2)%mod;
int x2=((a%mod)*((a+1)%mod)%mod)*getinv(2)%mod;
int y1=(((n%mod)*((n+1)%mod)%mod)*(((n%mod)*2LL%mod+1)%mod)%mod)*getinv(6)%mod;
int y2=(((a%mod)*((a+1)%mod)%mod)*(((a%mod)*2LL%mod+1)%mod)%mod)*getinv(6)%mod;
int x=((n+1)%mod)*((x1-x2+mod)%mod)%mod;
int y=(y1-y2+mod)%mod;
int res=(x-y+mod)%mod;
ans=(ans+res)%mod;
//cout<<res<<endl;
cout<<ans<<endl;
pause;
return 0;
}D - Sternhalma 2022ccpc威海
一共就19个格子,并且每个格子的权值是不会变的,所以可以记忆化加状压,这题就是一个带状压的记忆化搜索,但是实现雀氏有点难,直接看代码就可以
2022CCPC威海站 铜牌题解 A C D E G I J - 知乎 (zhihu.com)
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
#define lowbit(x) ((x)&(-x))
#define int long long
#define pause system("pause")
const int mod=998244353;
const int inf=1e18;
const int N = 1e6+100;
const double eps=1e-10;
int qpow(int a,int b)
{
int res=1;
while(b)
{
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int sgn(double x)
{
if(fabs(x)<eps) return 0;
else if(x<0) return -1;
else return 1;
}
int getinv(int a){return qpow(a,mod-2LL);}
int d[][2]={1,1,-1,-1,1,-1,-1,1,0,2,0,-2,2,0,-2,0};
int d2[][2]={-1,-1,1,1,-1,1,1,-1,0,-2,0,2,-2,0,2,0};
vector<pair<int,int>>coord=
{
{1,3},{1,5},{1,7},
{2,2},{2,4},{2,6},{2,8},
{3,1},{3,3},{3,5},{3,7},{3,9},
{4,2},{4,4},{4,6},{4,8},
{5,3},{5,5},{5,7}
};
int s[10][10],id[10][10],vis[N],f[N],n;
int tran(string s)
{
int res=0;
for(int i=0;i<s.length();i++)
{
int x=0;
if(s[i]=='#') x=1;
res+=x*(1<<i);
}
return res;
}
int dfs(int state)
{
if(vis[state]) return f[state];
int val=f[state];
for(int i=0;i<19;i++)
{
int x=(state>>i)&1;
if(x==0) continue;
int nstate=state&(~(1<<i));
val=max(val,dfs(nstate));
}
int g[10][10];
for(int i=0;i<19;i++)
{
auto [x,y]=coord[i];
g[x][y]=state>>i&1;
}
for(int i=0;i<19;i++)
{
if((state>>i&1)==0) continue;
auto [x,y]=coord[i];
for(int j=0;j<6;j++)
{
int ax=x+d[j][0],ay=y+d[j][1];
int bx=x+d2[j][0],by=y+d2[j][1];
if(ax<0||ay<0||bx<0||by<0) continue;
if(id[ax][ay]==-1||id[bx][by]==-1) continue;
if(g[ax][ay]==0||g[bx][by]==1) continue;
int nstate=state;g[ax][ay]=g[x][y]=0;g[bx][by]=1;
nstate=nstate&(~(1<<id[ax][ay]));
nstate=nstate&(~(1<<id[x][y]));
nstate=nstate|(1<<id[bx][by]);
val=max(val,dfs(nstate)+s[x][y]);
g[ax][ay]=g[x][y]=1;g[bx][by]=0;
}
}
vis[state]=1;
return f[state]=val;
}
signed main()
{
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
//freopen("in.txt","r",stdin);
memset(id,-1,sizeof(id));
for(int i=0;i<19;i++)
{
auto [x,y]=coord[i];
id[x][y]=i;
cin>>s[x][y];
}
vis[0]=1;
f[0]=0;
cin>>n;
for(int i=1;i<=n;i++)
{
string t="",g;
for(int j=1;j<=5;j++) cin>>g,t+=g;
int ans=dfs(tran(t));
cout<<ans<<endl;
}
pause;
return 0;
}