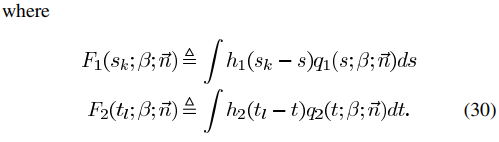1 介绍

• 等角圆柱形地图投影法

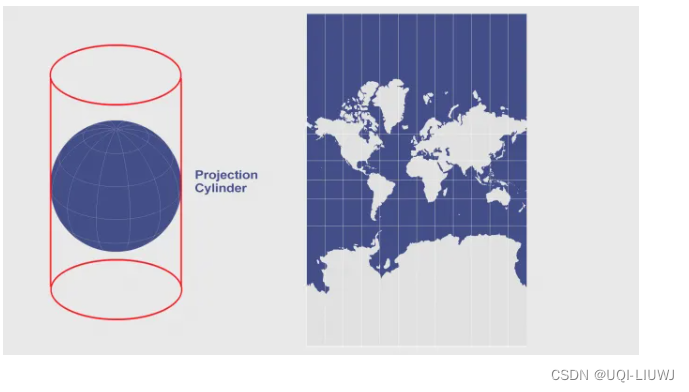
  • 假设地球被围在一个中空的圆柱里，其赤道与圆柱相接触，然后再假想地球中心有一盏灯，把球面上的图形投影到圆柱体上，再把圆柱体展开，这就是一幅标准纬线为零度（即赤道）的“墨卡托投影”绘制出的世界地图。

• 在以此投影法绘制的地图上，经纬线于任何位置皆垂直相交
  • ——>使世界地图可以绘制在一个长方形上。
• 大陆轮廓投影后的角度和形状不变（即等角）
  • “等角”也保证了方向和相互位置的正确性
    • ——>因此在航海和航空中常常应用
• 墨卡托投影会使面积产生变形，极点的比例甚至达到了无穷大。
• 经线间隔相同，纬线间隔从赤道向两级逐渐增大。

 

 

 2 特点

• 原来的经线都汇聚于极点，纬度愈高经线的间距愈小
  • 而在墨卡托投影上，经线是间隔相等的平行直线
• 地球表面上假想的各纬线间隔是相等的
  • 而在墨卡托投影上纬线间隔由赤道向两极逐渐扩大
• 墨卡托投影上经、纬线均为平行直线而且经纬线之间互相正交；
• 图上能正确表示航线与经线的夹角，例如航线在地球上与经线的夹角为15°，图上也表示为15°；
• 比例尺随纬度而变化，在一张地图上纬度不同，同一距离的比例尺也不同，不能比较面积。

下图是同样面积的圆在不同纬度的大小

 

3 Python 经纬度和墨卡托距离互换

 摩卡托坐标转经纬度坐标 - 鲲鹏数据在线工具 (site-digger.com)

3,1 墨卡托转经纬度

def Webmercater2latlon(mer_x,mer_y):
    lon_x=mer_x/20037508.34*180
    lon_y=mer_y/20037508.34*180
    
    lon_y=180/math.pi*(2*math.atan(math.exp(lon_y*math.pi/180))-math.pi/2)
    
    return(lon_x,lon_y)

Webmercater2latlon(13416225.028537776, 3555070.4333424848)
#(120.51999999999998, 30.400000000000016)

3.2 经纬度转墨卡托

def lonlat_to_Mercator_(lon,lon_y):
    x=lon*20037508.34/180
    y=math.log(math.tan((90 + lon_y) * math.pi / 360)) / (math.pi / 180)
    y=y*20037508.34/180    
    return x,y
lonlat_to_Mercator_(120.52,30.40)
#(13416225.028537776, 3555070.4333424848)