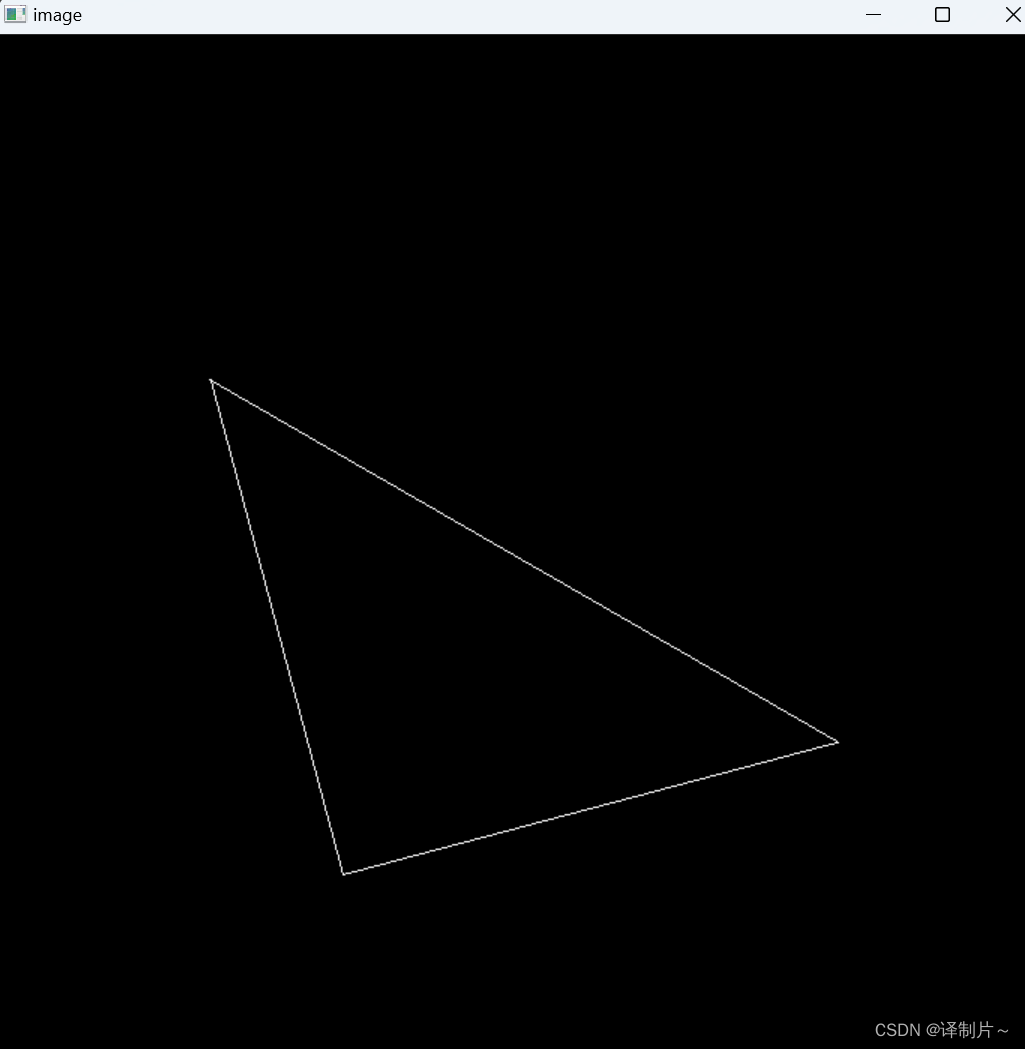
作业1的大致要求就是让我们实现如下两个函数，一个是返回在三维空间中绕着Z轴旋转的矩阵，另一个是返回投影矩阵。正确完成这两个函数之后，运行代码你就会在窗口中看到一个三角形，并且按a键和d键会发生旋转。

首先来实现get_model_matrix函数，在这个函数里只需要写出绕着Z轴旋转的旋转矩阵就行，下图是物体绕着X,Y,Z轴旋转的旋转矩阵公式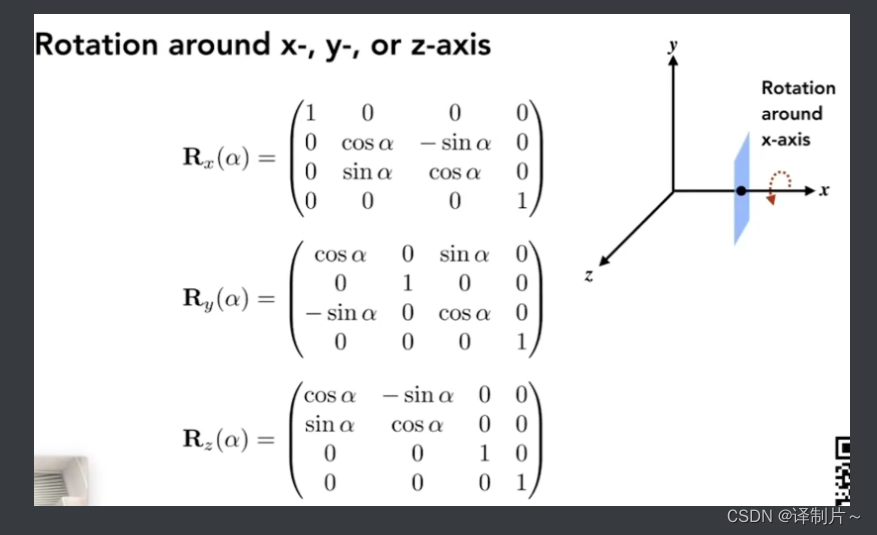
根据旋转矩阵的公式就可以直接写出对应的旋转矩阵，代码如下：

Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
    Eigen::Matrix4f model = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the model matrix for rotating the triangle around the Z axis.
    // Then return it.
    float angle = rotation_angle/180*acos(-1);
    //创建旋转矩阵
    model << cos(angle),-sin(angle),0,0,
        sin(angle),cos(angle),0,0,
        0,0,1,0,
        0,0,0,1;
    return model;
}

接着实现get_projection_matrix函数，在这个函数里需要创建透视投影矩阵。创建透视投影矩阵的过程是将透视变换为正交，在进行正交投影即可。该函数提供的参数eye_fov表示垂直可视角度，aspect_ratio表示宽高比，zNear表示相机与近平面的距离，zFar表示相机与远平面的距离。

• 透视变正交
  矩阵公式如下：
  

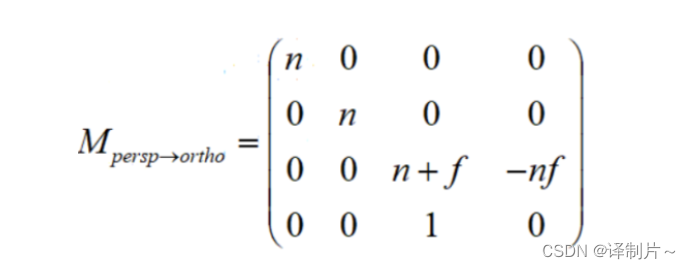
• 正交投影矩阵
  公式如下(先平移在缩放)：
  

  公式里面参数的意义如下：
  

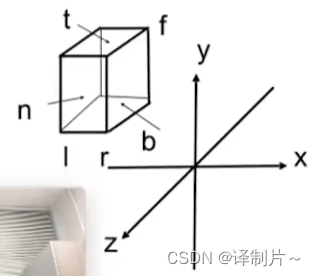
  在这里需要注意的是透视变为正交之后，l 和 r、t 和 b是关于原点对称的，所以公式中的 l + r = 0，t + b = 0，相当于沿着 Z 轴平移。

代码如下：

Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio,
                                      float zNear, float zFar)
{
    // Students will implement this function

    Eigen::Matrix4f projection = Eigen::Matrix4f::Identity();

    // TODO: Implement this function
    // Create the projection matrix for the given parameters.
    // Then return it.

    //创建透视变正交 矩阵
    Eigen::Matrix4f m = Eigen::Matrix4f::Identity();;
    m << zNear,0,0,0,
        0,zNear,0,0,
        0,0,zNear+zFar,-zNear*zFar,
        0,0,1,0;
    
    //创建正交投影矩阵
    Eigen::Matrix4f q1 = Eigen::Matrix4f::Identity(),q2 = Eigen::Matrix4f::Identity();
    //求出高度、宽度
    float height = tan(eye_fov/2/180*acos(-1)) * zNear * 2;  //height = t - b
    float width = height * aspect_ratio;  //width = r - l
    //缩放
    q1 << 2.0/width,0,0,0,
        0,2.0/height,0,0,
        0,0,2.0/(zNear - zFar),0,
        0,0,0,1;

    //平移
    q2 << 1,0,0,0,
        0,1,0,0,
        0,0,1,-(zNear+zFar)/2.0,
        0,0,0,1;

    projection = q1 * q2 * m;

    return projection;
}

默认结果如下：

按了三下d结果如下：