前言

本篇文章是对博客：从item-base到svd再到rbm，多种Collaborative Filtering(协同过滤算法)从原理到实现的补全，感谢该作者的分享

本文补全的内容为：

• SVD++中 $y_j$的实际含义理解，以及对应的梯度下降公式
• TimeSVD++梯度下降公式的分析

正文

SVD++

SVD++的原模型应该是如下形式：

其中$w_{ij}$是物品与物品的关联矩阵（梯度下降要学习的内容）
如果将$w_{ij}$再次进行QP分解，Q向量即物品i的隐向量，可与前式合并，得到如下形式：

即SVD++的公式模型
视上式中的所有字符为自变量求导，可得SVD++的梯度下降公式：

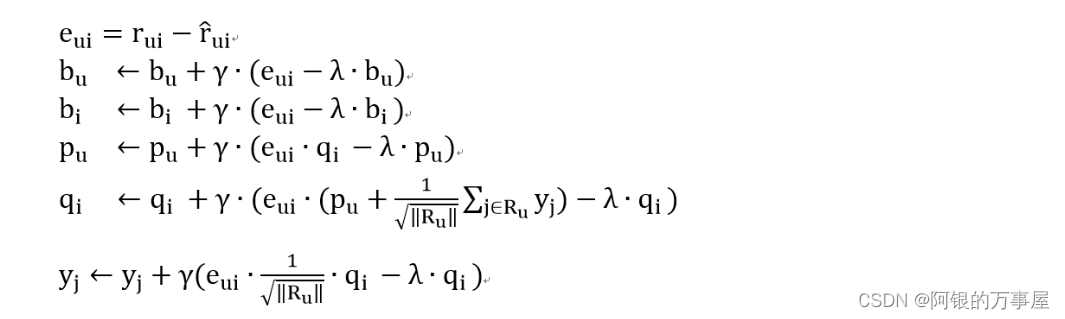
TimeSVD++

TimeSVD++的时序信息从基线预测模型和用户偏好模型两方面体现
一是基线预测模型，在SVD++的基础上，对$b_i$增加了电影的受欢迎度在30个时间区间下的波动常值（也就是30个待优化的参数），记为$b_{i,Bin(t)}$，修正后的$b_i$如下式：

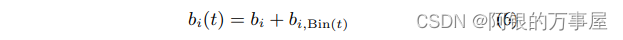
还对$b_u$增加了线性偏置量$de{v}_u(t)$以及用户$u$的波动常值$b_{u,t}$（原文中按天给，数据集一共40天，所以是40个待优化的参数），修正后的$b_u$如下式：

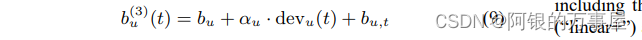
二是用户偏好模型，对$p_u$引入时间变量，按隐向量维度f分为：
p u ( t ) = { p u 1 ( t ) , . . . , p u f ( t ) } p_{u}(t)=\{p_{u1}(t),...,p_{uf}(t)\} pu​(t)={pu1​(t),...,puf​(t)}
对其中某一维k来说，引入的时间变量仍可按照线性偏置量以及用户$u$在该维度的波动常值来代替，即修正为下式：

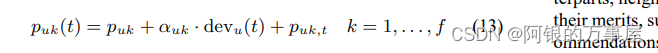
依向量化的思想，文中引入的新变量可以分为三类：

• $b_i$中的波动常值$b_{i,Bin(t)}$（有30个待优化量）
• $b_u$以及$p_u$中的线性偏置量（前者有3个待优化量，后者有3*f个待优化量）
• $b_u$以及$p_u$中的波动常值（前者有40个待优化量，后者有40*f个待优化量）

对上述三类新变量分别求梯度，与SVD++的梯度下降公式结合即可建立起TimeSVD++的梯度下降模型，其中：

• 波动常值可视作一个向量，对向量求梯度，而不是对每一个待优化量求梯度
• 线性偏置量因为3个带优化量有运算关系，应分别对3个待优化量求梯度，而不能视作向量求梯度