全连接层分析

对于神经网络为什么都能产生很好的效果虽然其是一个黑盒，但是我们也可以对其中的一些数学推导有一定的了解。

数学背景

$$目标函数为f=||max(XW,0)-Y|{|}_F^2，求\frac{\partial f}{\partial W},\frac{\partial f}{\partial X},\frac{\partial f}{\partial Y}$$

公式证明

$$\begin{array}{rl}解：& 首先我们假设替换变量\\ & f=||S-Y|{|}_F^2\\ & S=max(Z,0)\\ & Z=XW\\ & 根据假设变量，易得：\\ \frac{\partial f}{\partial S}& =\frac{\partial f}{\partial Y}=2(S-Y)\\ & \\ & (1)要求Z分量的偏导：\\ \partial f& =tr((\frac{\partial f}{\partial S}{)}^{T}dS)\\ & =tr((\frac{\partial f}{\partial S}{)}^{T}dmax(Z,0))\\ & =tr((\frac{\partial f}{\partial S}{)}^T\odot max\prime (Z,0)dZ)\\ & 所以：\\ \frac{\partial f}{\partial Z}& =max\prime (Z,0{)}^T\odot \frac{\partial f}{\partial S}\\ & =2\ast max\prime (Z,0)\odot (S-Y)\\ & =2\ast max\prime (Z,0)\odot (max(Z,0)-Y)\\ & \\ & (2)要求W分量的偏导:\\ \partial f& =tr(({\frac{\partial f}{\partial Z}}^{T}dZ)\\ & =tr((\frac{\partial f}{\partial Z}{)}^{T}d(XW))\\ & =tr((X^T\frac{f}{Z})dW)\\ & 所以：\\ \frac{\partial f}{\partial W}& =X^T\frac{\partial f}{\partial Z}\\ & =2\ast X^{T}max\prime (Z,0)\odot (max(Z,0)-Y)\\ & \\ & (3)要求X分量的偏导:\\ \partial f& =tr(({\frac{\partial f}{\partial Z}}^{T}dZ)\\ & =tr((\frac{\partial f}{\partial Z}{)}^{T}d(XW))\\ & =tr((\frac{f}{Z})W^{T}dX)\\ & 所以：\\ \frac{\partial f}{\partial X}& =W^T\frac{\partial f}{\partial Z}\\ & =2max\prime (Z,0)\odot (max(Z,0)-Y)W^T\end{array}$$

全连接ReLU

公式推导

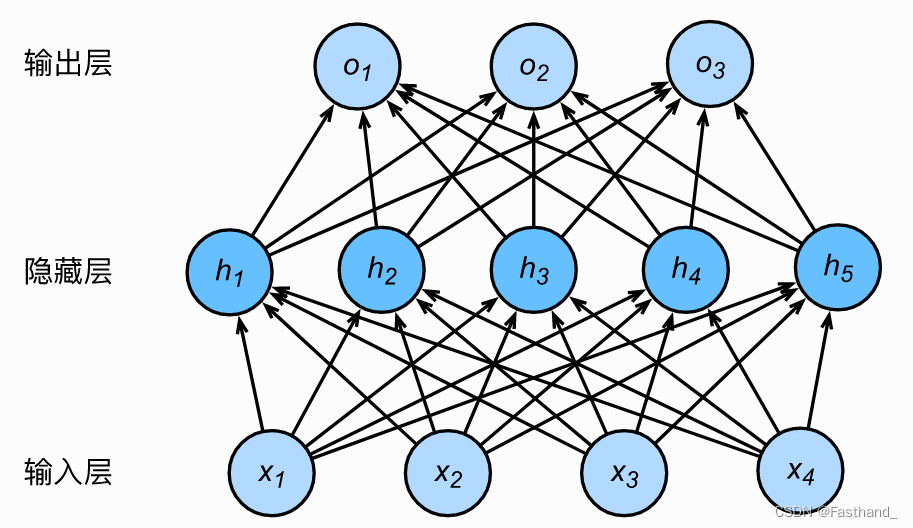
首先一个全连接ReLU神经网络，一个隐藏层，没有bias，用来从x预测y，使用L2 Loss。

$$\begin{array}{l}h=X{W}_1\\ h_{\text{relu }}=\max (0,h)\\ Y_{\text{pred }}=h_{\text{relu }}{W}_2\\ f={\Vert Y-Y_{\text{pred }}\Vert }_F^2\end{array}$$
其网络连接示意图如下所示：

对于$W_1$、$W_2$的偏导，由上数学背景易得为:
$$\begin{array}{rl}\frac{\partial f}{\partial Y_{pred}}& =2(Y-Y_{pred})\\ \frac{\partial f}{\partial W_2}& =h_{relu}^T.2(Y-Y_{pred})\\ \frac{\partial f}{\partial h_{relu}}& =\frac{\partial f}{\partial Y_{pre}}(W_2^T)\\ \frac{\partial f}{\partial h}& =max\prime (0,h)\frac{\partial f}{\partial h_{relu}}\\ \frac{\partial f}{\partial W_1}& =X^T\frac{\partial f}{\partial h}\end{array}$$

Numpy实现

import numpy as np
import torch
N,D_in,H,D_out = 64,1000,100,10
#随机数据
x = np.random.randn(N,D_in)
y = np.random.randn(N,D_out)
w1= np.random.randn(D_in,H)
w2= np.random.randn(H,D_out)

#学习率
learning_rate = 1e-6

for it in range(501):
    #Forward pass
    h = x.dot(w1)                #N*H
    h_relu = np.maximum(h,0)     #N*H
    Y_pred = h_relu.dot(w2)      #N*D_out
    
    #compute loss
    #numpy.square（）函数返回一个新数组，该数组的元素值为源数组元素的平方。 源阵列保持不变。
    loss = np.square(y-Y_pred).sum()
    #print(loss)
    if it%50==0:
        print(it,loss)
    
    #Backward pass
    #compute the gradient
    grad_Y_pre = 2.0*(Y_pred - y)
    grad_w2 = h_relu.T.dot(grad_Y_pre)
    grad_h_relu = grad_Y_pre.dot(w2.T)
    grad_h = grad_h_relu.copy()
    grad_h[h<0] = 0
    grad_w1 = x.T.dot(grad_h)
    
    #update weights of w1 and w2
    w1 -= learning_rate * grad_w1
    w2 -= learning_rate * grad_w2

全连接层练习2

$$\begin{array}{l}h=X{W}_1+b_1\\ h_{\text{sigmoid }}=\mathrm{sigmoid}(h)\\ Y_{\text{pred }}=h_{\text{sigmoid }}{W}_2+b_2\\ f={\Vert Y-Y_{\text{pred }}\Vert }_F^2\end{array}$$
![[激活函数#sigmoid函数]]

由上公式易得：
$$\begin{array}{rl}\frac{\partial f}{\partial Y_{pred}}& =2(Y-Y_{pred})\\ \frac{\partial f}{\partial h_{sigmoid}}& =\frac{\partial f}{\partial Y_{pred}}{W}_2^T\\ \frac{\partial f}{\partial h}& =\frac{\partial f}{\partial h_{sigmoid}}sigmoid\prime (x)\\ & =\frac{\partial f}{\partial h_{sigmoid}}sigmoid(x)(1-sigmoid(x))\\ \frac{\partial f}{\partial W_2}& =h_{sigmoid}^T\frac{\partial f}{\partial Y_{pred}}\\ \frac{\partial f}{\partial b_2}& =\frac{\partial f}{\partial Y_{pred}}\\ \frac{\partial f}{\partial W_1}& =X^T\frac{\partial f}{\partial h_{sigmoid}}\\ \frac{\partial f}{\partial b_1}& =\frac{\partial f}{\partial h}\end{array}$$

%matplotlib inline
import torch
import torch.nn.functional as F
import matplotlib.pyplot as plt

torch.manual_seed(1)    # reproducible

x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)  # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size())


plt.scatter(x.numpy(), y.numpy())

class Net(torch.nn.Module):
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()
        self.linear1 = torch.nn.Linear(n_feature,n_hidden,bias=True)
        self.linear2 = torch.nn.Linear(n_hidden,n_output,bias=True)

    def forward(self, x):
        y_pred = self.linear2(torch.sigmoid(self.linear1(x)))
        return y_pred
net = Net(n_feature=1, n_hidden=20, n_output=1)     # define the network
print(net)  # net architecture
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)
loss_func = torch.nn.MSELoss()  # this is for regression mean squared loss

plt.ion()   # something about plotting

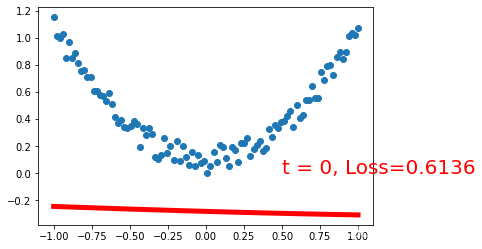
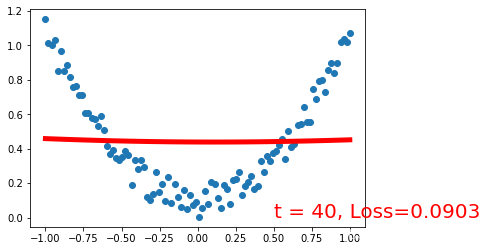
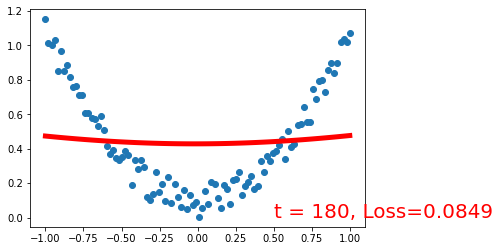
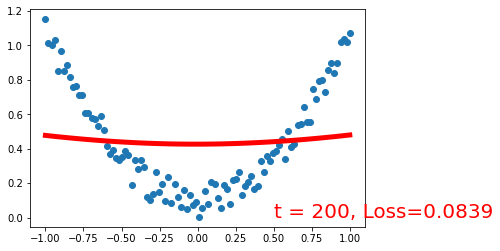
for t in range(201):
    prediction = net(x)     # input x and predict based on x
    loss = loss_func(prediction, y)     # must be (1. nn output, 2. target)

    optimizer.zero_grad()   # clear gradients for next train
    loss.backward()         # backpropagation, compute gradients
    optimizer.step()        # apply gradients

    if t % 20 == 0:
        # plot and show learning process
        plt.cla()
        plt.scatter(x.numpy(), y.numpy())
        plt.plot(x.numpy(), prediction.data.numpy(), 'r-', lw=5)
        plt.text(0.5, 0, 't = %d, Loss=%.4f' % (t, loss.data.numpy()), fontdict={'size': 20, 'color':  'red'})
        plt.pause(0.1)
        plt.show()

plt.ioff()
plt.show()