目录

前言：

1.汉诺塔：

1.1分析盘子数从1-3的情况

1.2盘子移动的规律总结

2.青蛙跳台阶：

2.1跳一个台阶或跳两个台阶

2.2扩展

---

❤博主CSDN:啊苏要学习

  ▶专栏分类：C语言◀

  C语言的学习，是为我们今后学习其它语言打好基础，C生万物！

  开始我们的C语言之旅吧！✈

---

前言：

1.汉诺塔：

  在学习完递归后，我们扩展练习一些与递归相关的题目。这些听上去很难，实际上是可以通过一步一步分析，总结规律做出来的抽象题。

  汉诺塔（也称河内塔）起源于印度印度古老传说的一个益智游戏。大梵天创造世界的时候，做了三根金刚石柱，在一根柱子上从上往下叠着从小到大的黄金圆盘，我们假设是A柱。

  游戏规则是这样的：我们需要把圆盘全部移动到C柱上，每次只能一个一个盘的移动，并且需要保证小的盘不能出现在大盘的下方。

1.1分析盘子数从1-3的情况

  第一种：直接将A上的盘子移动到C上，步骤为A->C。

  第二种：把底盘的上一个盘子移动到B柱上；再将底盘移动到C柱上；最后把B柱上的盘子移动到C柱上；A->B；A->C；B->C；

  第三种：抽象理解就是：底盘上的所有盘子被我们移动到B盘上；然后将底盘移动到C盘上；

---

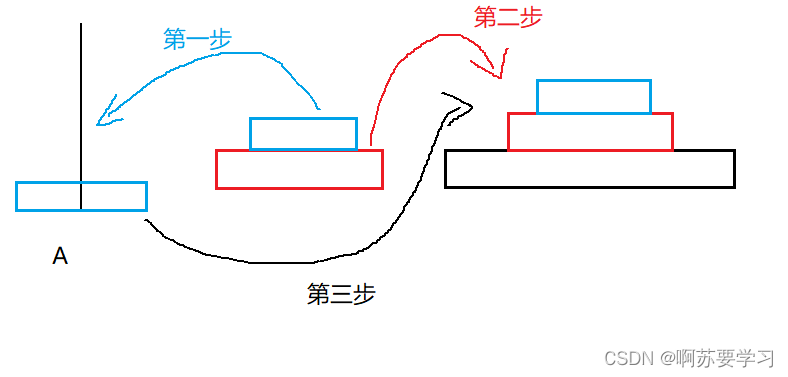
  接着抽象的理解就是：将B柱上所有的盘子，移动到C柱子上；

1.2盘子移动的规律总结

  盘子数从1到3，分析移动的次数：1个盘子的时候，移动了1次（2^1 - 1），2个盘子的时候，移动了3次（2^2 - 1），3个盘子的时候移动了7次（2^3 - 1）；由此递推，移动盘子的次数与盘子数的关系是2^n - 1，n是盘子的个数。

  1.只有一个盘子的时候，将底盘移动到C柱上。我们得知，如果A柱上已经只剩最大的盘子了，我们需要执行操作A->C。

2.有两个盘子的时候，我们需要将底盘上的盘子移动到B柱上，让A柱剩下最大的底盘，依旧执行A->C这一步骤；B柱上的1个盘子，和在A柱上只有1个盘子是一样的道理，因为它头顶上没有盘子，直接移动到C就可以了。

3.有三个盘子的时候，我们需要将底盘上的两个盘子，借助C柱的帮助，移动到B柱上，然后第三个盘子执行A->C。此时B柱上有两个盘子，与A柱盘子数为2的情况一致，只不过是在B柱上。我们最终的目的是需要将B柱上的两个盘子移动到C上。在A柱两个盘子的时候，借助B柱完成移动到C，在B柱两个盘子同理，借助A柱完成移动到C。

  所以由这三种情况分析得：假设现在盘子数为N，在我们需要将A柱上的第N个盘子上面N-1个盘子移动到B柱上（借助C柱，请参考n = 2的分析）--->将第N个盘子移动到C柱上（请参考n = 1 的分析）--->将总共N-1个盘子从B柱上移动到C柱上。

•   Hanoi(n - 1, A, C, B)的意思是，将A柱上n-1个盘子，借助C柱，移动到B柱上；

•   move(A, C)将A柱上，最大的盘子移动到C柱上；

•   Hanoi(n - 1, B, A, C)的意思是，将B柱上n-1个盘子，借助A柱，移动到C柱上； 

  递归的思想是，将大事化小。Hanoi（）函数的本质是想将A柱上的盘借助B柱转移到C柱上。在这个过程中，分成上面的三个步骤完成，大家感兴趣可以写出这段代码后，研究递归过程中的步骤，学会玩汉诺塔游戏。

2.青蛙跳台阶：

2.1跳一个台阶或跳两个台阶

  一只小青蛙，来到一个有N个台阶的楼梯，这只小青蛙每次只能跳一个台阶或两个台阶，试问青蛙有多少种跳法跳到第N个台阶。

  当N = 1时，小青蛙跳一步就到了。一种跳法

  当N = 2时，小青蛙可以选择一步一步跳；也可以一次性跳两步；。两种跳法

  当N = 3时，小青蛙的第一次起跳至关重要！当小青蛙跳选择跳一个台阶，那么接下来小青蛙面对的是两个台阶，此时对这两个台阶的跳法是N = 2时的跳法，有两种。当小青蛙选择跳两个台阶，那么剩下的一个台阶就是小青蛙在面对一个台阶时候的跳法，有一种。所以当N = 3时，总共有三种跳法

  当N = 4时，同N = 3时分析一样，第一步小青蛙的选择，就决定了后续，类似于数学中的分类加法~。当小青蛙跳一个台阶，面对的是N = 3的台阶，有三种跳法；当小青蛙跳两个台阶，面对的是N = 2的台阶，有两种跳法；所以当N = 4时，总共有5种跳法

  总结，如果N为1，跳法只有一种；如果N为2，跳法为两种；如果N为3，跳法为前两种跳法的和，跳法为三种；依次类推，可以得知小青蛙是一只懂得斐波那契数列的聪明小青蛙。

  JumpWay是求青蛙跳N个台阶的跳法函数，当N等于三时，return JumpWay(2) + JumpWay(1)的意思是，求小青蛙在跳两个台阶、跳一个台阶这两种情况的次数和，符合我们需要的预期，也是正确的~

2.2扩展

  忽然有一天，青蛙跳台阶的能力变强了，小青蛙不仅可以跳两个台阶，三个台阶也行，此时跳到N个台阶又有多少中跳法呢？其实这个规律也可以分析出来，请看：

  当N = 1时，一种跳法。

  当N = 2时，两种跳法。

  当N = 3时，JumpWay(2) + JumpWay(1)  + 1(直接一步到胃！)，四种跳法。

  当N = 4时，JumpWay(3) + JumpWay(2)  + JumpWay(1)，七种跳法。

  因为N=4时，小青蛙选择跳三个台阶，面对他的是N=1时的情况，就有多一种跳法啦。

  规律是：N = 3时多一种跳法，往后的台阶，跳法等于前三种台阶的跳法和。

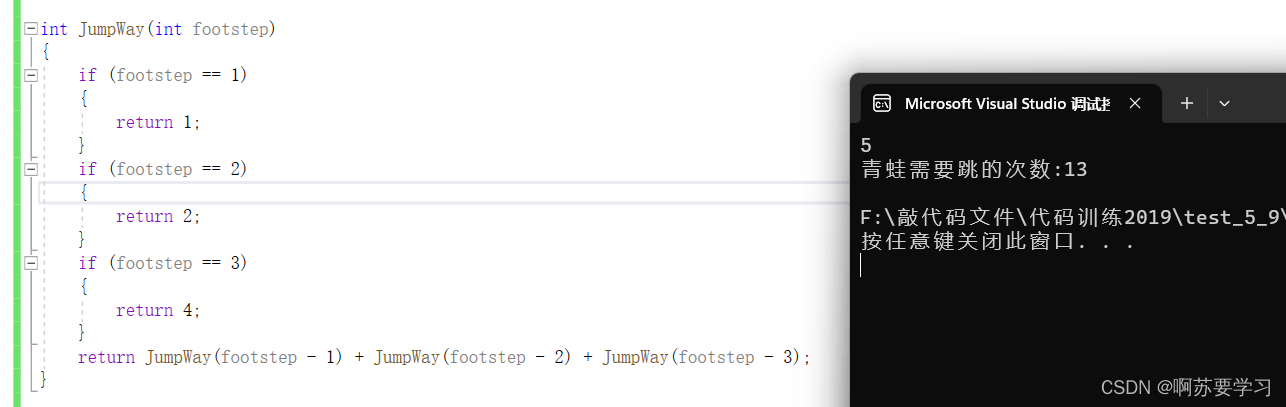
   7+4+2 = 13种

  好啦，汉诺塔和小青蛙都要和我们说拜拜啦！希望读者读完能有所理解，掌握问题的本质，即使细节比较难懂，也期望思想上对这些问题有认知。

---

结语：希望读者读完有所收获！在学C的路上，祝福我们能越来越C!✔

  读者对本文不理解的地方，或是发现文章在内容上有误等，请在下方评论区留言告诉博主哟~，也可以对博主提出一些文章改进的建议，感激不尽！最后的最后！

  ❤求点赞，求关注，你的点赞是我更新的动力，一起努力进步吧。