目录
心脏病患病影响因素探究
一、研究目的
二、数据来源和相关说明
三、描述性统计分析
四、数据建模
4.1 全模型
(1)模型构建
(2)模型预测
4.2 基于AIC准则的选模型A
4.3 基于BIC准则的选模型B
4.4 模型评估
五、结论及建议
5.1 结论
5.2 建议
六、代码
心脏病患病影响因素探究
内容提要:本文基于R语言faraway包中的wcgs数据集,分析心脏病患病影响因素。被调查人群中,有8.1%的人患有心脏病,91.9%的人未患心脏病。全模型中,变量age、sdp、chol、cigs和timechd对是否患心脏病有显著影响,age、sdp、chol和cigs的增加都会增加患心脏病的优势,而timechd会降低患心脏病的优势比。用全模型预测前十位受访者患病概率,分界点α=0.5 时,MCR=0.2 ;分界点α=0.7 时,MCR=0.1 。全模型,AIC模型和BIC模型中,AIC模型效果最好。
一、研究目的
分析心脏病患病影响因素,对预防心脏病的发生具有重要意义。本文欲通过建立logistic回归模型,分析心脏病的影响因素,为心脏病的预防贡献微薄之力。
二、数据来源和相关说明
数据来源于R语言faraway包中的wcgs数据集,其中包含3154条数据。这是某机构调查的3154个健康男人,介于39-59岁,8年后看他们是否得了心脏病,并且收集了一些可能导致心脏病的自变量数据,得到了数据集wcgs。数据集包含13个变量——age、height、weight、sdp、dbp、chol、behave、cigs、dibep、chd、typechd、timechd、arcus,其中有5个分类型变量,8个连续型变量。本文欲探究变量chd(冠心病)的影响因素。
三、描述性统计分析
为了获得对数据的整体了解,本文先对数据集中的变量chd、weight和cigs进行了描述性统计分析,得到了图3-1到图3-4的图形。

图3-1 是否患有冠心病
由图3-1可以得出:91.9%的人未患心脏病,8.1%的人患有心脏病。
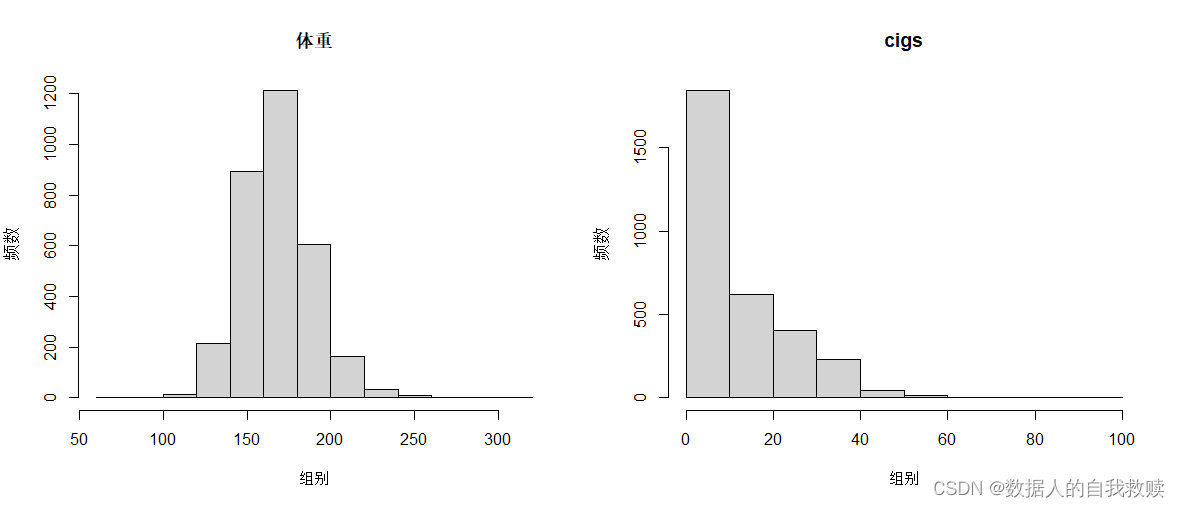
图3-2 weight和cigs直方图
由图3-2可以得出:weight整体服从正态分布,大多集中在150-200之间;cigs大致服从指数分布,最多集中在0-10范围内。

图3-3 箱线图
由图3-3可以得出:体重与吸烟量在是否有心脏病上都存在一定的差异性。患心脏病的人体重的最大值低于不患心脏病的人,患心脏病的人体重的最低值高于不患心脏病的人,即患心脏病的人体重极值要小于不患心脏病的人。不患心脏病的人的吸烟数明显低于患心脏病的人,即可以猜测患心脏病可能与吸烟数有关。
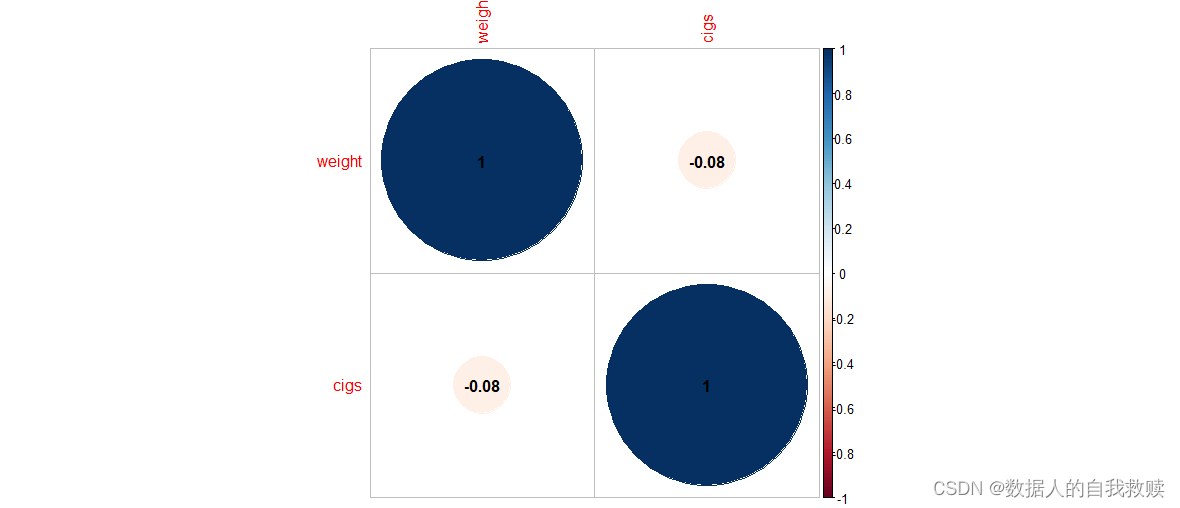
图3-4 weight-cigs热力图
由图3-4可以得出:体重和吸烟数几乎不存在线性相关关系。
四、数据建模
4.1 全模型
(1)模型构建
为了分析心脏病的影响因素,本文建立了二元logistic回归模型。考虑将所有变量均纳入模型,但在参数估计时无法收敛,因此考虑剔除一些变量后再进行参数估计,得到表4-1的参数估计结果。
表4-1 全模型参数估计结果
| 变量 | Estimate | Std.Error | z value | Pr(>|z|) |
| (Intercept) | -9.29E+00 | 2.67E+00 | -3.474 | 0.000513*** |
| age | 6.47E-02 | 1.38E-02 | 4.694 | 2.68e-06*** |
| height | 3.25E-02 | 3.85E-02 | 0.845 | 0.39792 |
| weight | 5.44E-03 | 4.37E-03 | 1.245 | 0.213257 |
| sdp | 1.93E-02 | 7.36E-03 | 2.622 | 0.008738** |
| dbp | -1.46E-02 | 1.23E-02 | -1.193 | 0.232941 |
| chol | 1.14E-02 | 1.74E-03 | 6.565 | 5.20e-11*** |
| as.factor(behave)A2 | 9.15E-02 | 2.57E-01 | 0.357 | 0.721439 |
| as.factor(behave)B3 | -3.63E-01 | 2.77E-01 | -1.311 | 0.189705 |
| as.factor(behave)B4 | -2.41E-01 | 3.57E-01 | -0.676 | 0.49921 |
| cigs | 1.53E-02 | 4.98E-03 | 3.066 | 0.002169** |
| timechd | -1.53E-03 | 8.44E-05 | -18.094 | <2e-16*** |
由表4-1可以得出:
- 变量age、sdp、chol、cigs和timechd对是否患心脏病有显著影响,其他变量无显著影响。
- 其他自变量不变时,每天吸烟量增加一根,患心脏病的优势会变为之前的1.0154倍;若患心脏病的概率很小,则可以近似认为吸烟量每增加一根,患心脏病的概率变为之前的1.0154倍。
- 其他自变量不变时,age每增加一岁,患心脏病的优势会变为之前的1.0669倍;sdp每增加一,患心脏病的优势会变为之前的1.0195倍;chol每增加一,患心脏病的优势会变为之前的1.0115倍;timechd每增加一,患心脏病的优势会变为之前的0.9985倍,即会降低患心脏病的优势比。上述在统计学上均显著。
- height每增加一,患心脏病的优势会变为之前的1.0331倍;weight每增加一,患心脏病的优势会变为之前的1.0055倍;dbp每增加一,患心脏病的优势会变为之前的0.9855倍,即会降低患心脏病的优势比;与A1相比,A2患心脏病的优势比是其1.0958倍,B3是其0.6952倍,B4是其0.7858倍。上述在统计学上均不显著。
(2)模型预测
基于全模型,可以预测前十位受访者的患病概率,预测结果如表4-2所示。
表4-2 全模型预测结果
| 样本 | 预测概率 | 真实值 | α=0.5 | α=0.7 |
| 1 | 0.1961 | 0 | 0 | 0 |
| 2 | 0.018939 | 0 | 0 | 0 |
| 3 | 0.004255 | 0 | 0 | 0 |
| 4 | 0.004289 | 0 | 0 | 0 |
| 5 | 0.293788 | 1 | 0 | 0 |
| 6 | 0.013297 | 0 | 0 | 0 |
| 7 | 0.006133 | 0 | 0 | 0 |
| 8 | 0.008294 | 0 | 0 | 0 |
| 9 | 0.01238 | 0 | 0 | 0 |
| 10 | 0.529694 | 0 | 1 | 0 |
由表4-2可以得出:当分界点α=0.5 时,十位受访者的MCR 为MCR=0.2 ;当分界点α=0.7 时,十位受访者的MCR 为MCR=0.1 。
4.2 基于AIC准则的选模型A
基于AIC准则对全模型的变量进行选择,得到选模型A,模型参数估计值如表4-3所示。
表4-3 选模型A的参数估计
| 变量 | Estimate | Std.Error | z value | Pr(>|z|) |
| (Intercept) | -7.43E+00 | 1.09E+00 | -6.836 | 8.14e-12*** |
| age | 6.38E-02 | 1.38E-02 | 4.635 | 3.57e-06*** |
| weight | 6.52E-03 | 3.55E-03 | 1.835 | 0.066501· |
| sdp | 1.20E-02 | 4.68E-03 | 2.556 | 0.010583* |
| chol | 1.12E-02 | 1.73E-03 | 6.5 | 8.01e-11**** |
| as.factor(behave)A2 | 1.22E-01 | 2.56E-01 | 0.476 | 0.634303 |
| as.factor(behave)B3 | -3.38E-01 | 2.77E-01 | -1.223 | 0.221504 |
| as.factor(behave)B4 | -2.14E-01 | 3.57E-01 | -0.6 | 0.548701 |
| cigs | 1.65E-02 | 4.90E-03 | 3.362 | 0.000775*** |
| timechd | -1.52E-03 | 8.38E-05 | -18.086 | <2e-16*** |
由表4-3可以得出:选模型A保留了变量age、weight、sdp、chol、behave、cigs和timechd。在显著性水平α=0.05 下,除了变量weight和behave,其他变量都具有统计学显著性。
4.3 基于BIC准则的选模型B
基于BIC准则对全模型的变量进行选择,得到选模型B,模型参数估计值如表4-4所示。
表4-4 选模型B的参数估计
| 变量 | Estimate | Std.Error | z value | Pr(>|z|) |
| (Intercept) | -6.71E+00 | 8.94E-01 | -7.484 | 7.21e-14*** |
| age | 6.44E-02 | 1.36E-02 | 4.745 | 2.08e-06*** |
| sdp | 1.48E-02 | 4.47E-03 | 3.318 | 0.000908*** |
| chol | 1.12E-02 | 1.70E-03 | 6.557 | 5.49e-11*** |
| cigs | 1.66E-02 | 4.88E-03 | 3.402 | 0.000670*** |
| timechd | -1.55E-03 | 8.33E-05 | -18.558 | <2e-16*** |
由表4-4可以得出:选模型B保留了变量age、sdp、chol、cigs和timechd,这些变量在显著性水平α=0.05 下都具有非常高的统计学显著性。
4.4 模型评估
以前80%的样本作为训练集,后20%的样本作为测试集,分别用训练集拟合全模型、AIC准则和BIC准则进行变量筛选的模型,用测试集做ROC曲线和AUC箱线图,得到图4-1和图4-2。
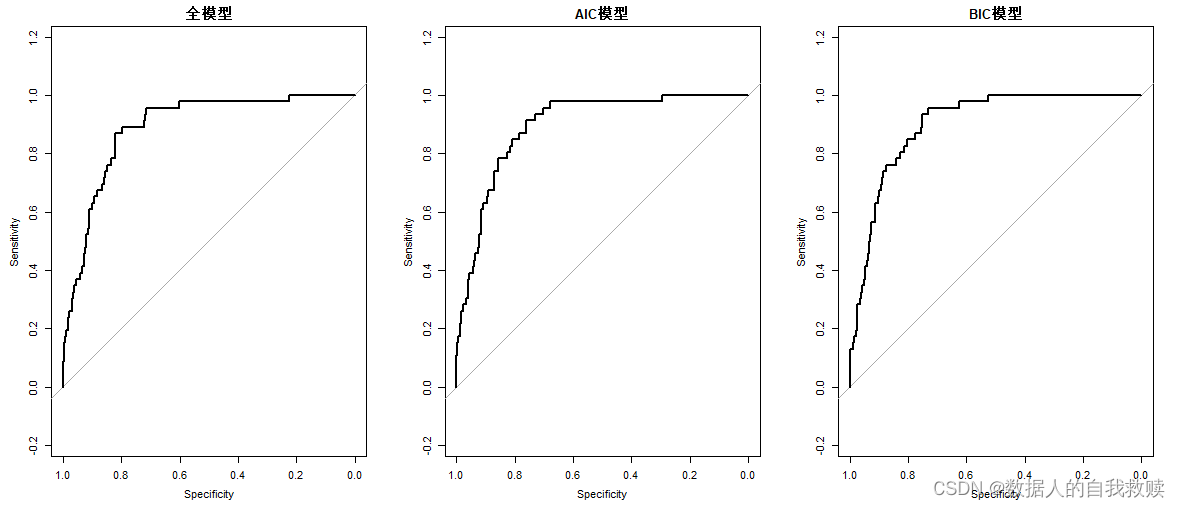
图4-1 三个模型ROC曲线
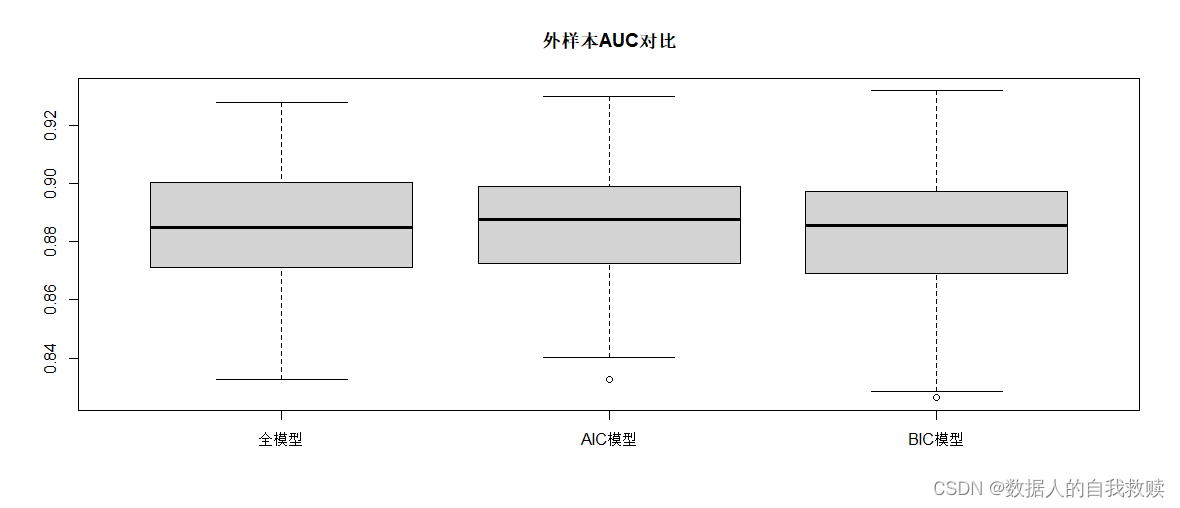
图4-2 三个模型AUC箱线图
由图4-1和图4-2可以得出:无论是ROC曲线,还是AUC箱线图,三个模型的分类效果差异较小,其中AIC模型效果最好。
五、结论及建议
5.1 结论
- 被调查人群中,有8.1%的人患有心脏病,91.9%的人未患心脏病,患心脏病的概率较低;被调查人群的体重近似服从正态分布,吸烟数近似服从指数分布;患心脏病人群的吸烟数明显多于不患心脏病人群。
- 变量age、sdp、chol、cigs和timechd对是否患心脏病有显著影响,其他变量无显著影响。
- 其他自变量不变时,age每增加一岁,患心脏病的优势会变为之前的1.0669倍;sdp每增加一,患心脏病的优势会变为之前的1.0195倍;chol每增加一,患心脏病的优势会变为之前的1.0115倍;timechd每增加一,患心脏病的优势会变为之前的0.9985倍,即会降低患心脏病的优势比。上述在统计学上均显著。
- 全模型,基于AIC准则的选模型A、基于BIC准则的选模型B中,选模型A的分类效果最好。
5.2 建议
吸烟和喝酒都会在一定程度上增加患心脏病的概率,因此为了自身身体健康,建议少吸烟,少喝酒。
六、代码
library(faraway)
attach(wcgs)
wcgs[c(1:5),]
summary(chd)
#统计chd(冠心病)情况
x=c(2897,257)
color=c('red','orange')
piepercent1=round(100*x/sum(x),1)
pie(x,labels=piepercent1,main="是否患有冠心病",col=color)
legend("topright",c("否","是"),cex=1.5,fill=color)
#绘制变量weight和cigs的直方图
par(mfrow=c(1,2))
hist(weight,main="体重",xlab="组别" ,ylab = "频数")
hist(cigs,main="cigs",xlab="组别" ,ylab = "频数")
#绘制冠心病与weight、cigs的箱线图
par(mfrow=c(1,2))
boxplot(weight~chd,ylab="体重",xlab="是否患有冠心病",data=wcgs,names=c("否","是"))
boxplot(cigs~chd,ylab="cigs",xlab="是否患有冠心病",data=wcgs,names=c("否","是"))
#连续变量之间相关性热力图
library(corrplot)
b=wcgs[,c(3,8)]
k=cor(b,use='everything',method='pearson')
par(mfrow=c(1,1))
corrplot(k,addCoef.col = "black")
#全模型
model.full=glm(chd~age+height+weight+sdp+dbp+chol+as.factor(behave)+cigs+timechd
,family=binomial(link=logit),data=wcgs,maxit=50)
#模型结果,不显著的变量也要解读,加上不具有统计学意义
summary(model.full)
#似然比卡方检验模型整体效果
1-pchisq(30.56,df=7)
pred=predict(model.full,wcgs)
pred
#基于AIC准则下变量的选择
c(AIC(model.full),BIC(model.full))
model.aic=step(model.full,trace = F)
summary(model.aic)
ss=length(wcgs[,1])#样本量
#基于BIC准则下变量的选择
model.bic=step(model.full,trace = F,k=log(ss))
summary(model.bic)
#只留了特别显著的变量
library(pROC)
#多次模拟,去除随机误差的影响(了解即可)
nsimu=100#进行100次模拟
p=0.8#用作训练集的样本概率
ss0=round(ss*p)#训练集样本量
AUC=as.data.frame(matrix(0,nsimu,3))#100行,3列的零数据框
names(AUC)=c("全模型","AIC模型","BIC模型")
#开始模拟
for(i in 1:nsimu){
#打乱a样本顺序,随即编号并排序
aa=wcgs[order(runif(ss)),]
#数据集aa的前70%作为训练集
A0=aa[c(1:ss0),]
#数据集aa的后30%作为测试集
A1=aa[-c(1:ss0),]
model.1=glm(chd~age+height+weight+sdp+dbp+chol+as.factor(behave)+cigs+timechd,family=binomial(link=logit),data=A0)
model.2=glm(chd~age+weight+sdp+chol+as.factor(behave)+cigs+timechd,family=binomial(link=logit),data=A0)
model.3=glm(chd~age+sdp+chol+cigs+timechd,family=binomial(link=logit),data=A0)
#测试集检验模型效果,计算预测值
pred.1=predict(model.1,A1)
pred.2=predict(model.2,A1)
pred.3=predict(model.3,A1)
#计算AUC值
y=A1$chd
auc.1=roc(y,pred.1)$auc
auc.2=roc(y,pred.2)$auc
auc.3=roc(y,pred.3)$auc
#将各个AUC值填充到零矩阵中
AUC[i,]=c(auc.1,auc.2,auc.3)
}
#绘制箱线图看三个模型的AUC分布情况,AUC越大,模型分类效果越好
par(mfrow=c(1,1))
boxplot(AUC,main="外样本AUC对比")
#利用最后一次模拟数据绘制三个模型的ROC曲线
#计算混淆矩阵
roc.1=roc(y,pred.1)
roc.2=roc(y,pred.2)
roc.3=roc(y,pred.3)
#绘制三条ROC曲线,比较效果
par(mfrow=c(1,3))
plot(roc.1,main="全模型")
plot(roc.2,main="AIC模型")
plot(roc.3,main="BIC模型")
个人意见,还请各位读者批评指正!