一、算法目的

量子隐形传态，又称量子遥传、量子隐形传输、量子隐形传送、量子远距传输或量子远传，是一种利用分散量子缠结与一些物理讯息的转换来传送量子态至任意距离的位置的技术，这是一种全新的通信方式。它传输的不再是经典信息而是量子态携带的量子信息，在量子纠缠的帮助下，待传输的量子态如同经历了科幻小说中描写的“超时空传输”，在一个地方神秘地消失，不需要任何载体的携带，又在另一个地方神秘地出现，就像三体小说的那两个“智子”，就是通过量子传输的形式进行控制。

具体的例子如下：

我们假设程序员小李在武汉，想把量子信息发送给在苏州的伍老师，具体地说，假设他想给伍老师发情书，这份情书的内容被存储在了 $|\varphi >=\alpha |0>+\beta |1>$ 中。伍老师想要得到准确的信息，这需要小李能够准确的传递关于α和β的信息。

但是小李程序员不能简单地生成一个| $\varphi$ >的副本然后传送给伍老师，因为复制状态只有在经典计算中生效，而对量子态不合宜，这个感兴趣的同学可以学一学量子不可克隆原理。

所以小李程序员就开始头秃啦，他迫切的想要伍老师知道自己的这份爱意。然而，办法总比困难多，量子仿佛看出来了小李浓烈的爱意，构造出来了一个能传递信息的算法，于是通过两个经典位和纠缠，小李可以转换状态| $\varphi$ > ，把情书传递给伍老师。那么如何传递，让我们通过后面的算法学习吧！

二、算法原理

将需要传递的第三个量子比特的信息，即“情书，”赋予EPR对中的第一个量子比特上，传输给伍老师，即将qubits[2]的信息传递到目标比特qubits[0]上。

我们还是先给电路，再来推算这个电路的合理性。

这次要使用的量子线路里面有一部是制造Bell态的线路，qubits[1]是控制比特，qubits[0]是目标比特，而我们希望把新加入的qubits[2]的信息传递到qubits[0]上。假设qubits[2]的信息是| $\varphi$ >，即用|0>态经过RY门可以得到，其中RY的矩阵形式为：

$RY(\theta )=e^{ \frac{-i\theta Y}{2}}=cos(\frac{\theta }{2})I-isin(\frac{\theta }{2})Y=\begin{pmatrix} cos(\frac{\theta }{2})&-sin(\frac{\theta }{2}) \\ -sin(\frac{\theta }{2}) & cos(\frac{\theta }{2}) \end{pmatrix}$

然后，我们需要对qubits[2]与qubits[1]这个EPR对执行Bell测量，具体的步骤为：对这一对量子执行CNOT门操作，qubits[2]是控制比特，qubits[1]是目标比特，随后让qubits[2]门进行H门操作，随后在计算基上测量它们。

测量之后，qubits[2]、qubits[1]现在有4种测量结果，即|00>,|01>,|10>,|11>。当测量结果处于不同状态时，对qubits[2]进行不同的门操作。如下表：

qubits[2]、qubits[1]处于的量子态	对qubits[0]的操作
\|0>\|0>	无操作
\|0>\|1>	经过一个Z门
\|1>\|0>	经过一个X门
\|1>\|1>	线经过一个X门，再经过一个Z门

这样的算子可以使qubits[0]获得qubits[2]的信息！

其电子线路图如下：其中qubits[0]与qubits[1]构成了上一题的贝尔态。

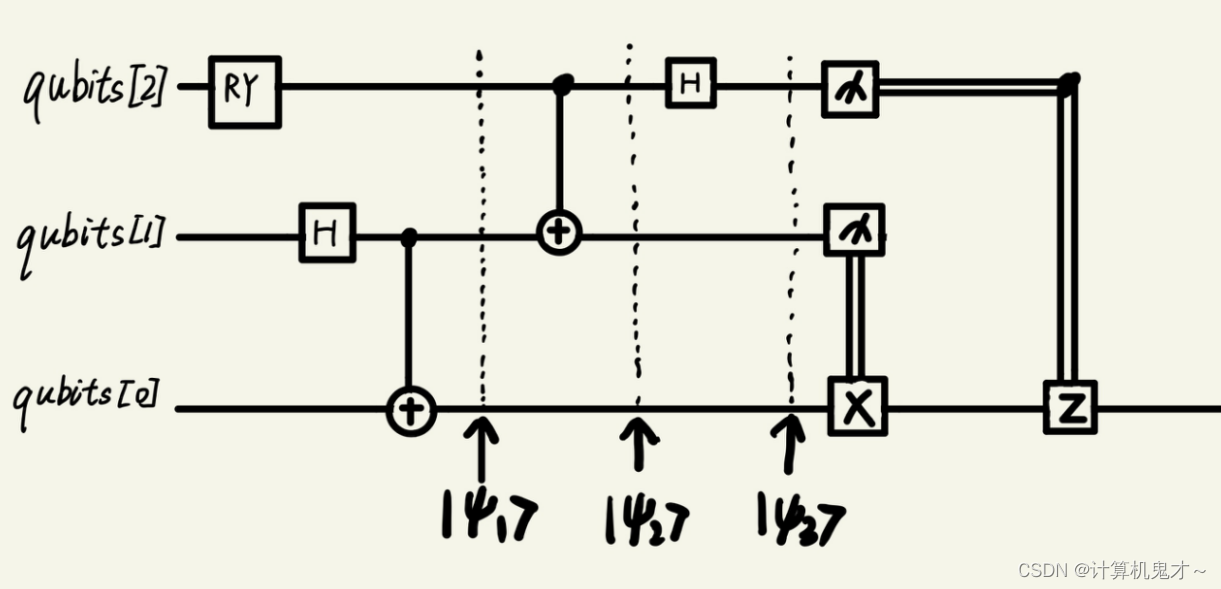
我们来推理一下，三个qubits初始态均为|0>,qubits[2]经过RY之后，我们得到需要量子隐形传态的状态 $|\varphi >=\alpha |0>+\beta |1>$ ，其中 $\alpha$ 与 $\beta$ 均为未知的振幅。同时由第一问的贝尔态问题我们知道了qubits[1]与qubits[0]的状态。那么，我们可以求出| $\varphi _{1}$ >的状态：

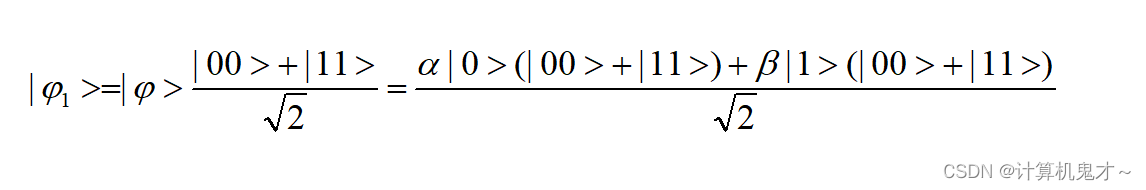
再经过qubits[2]与qubits[1]的控制门后，我们能得到| $\varphi _{2}$ >的状态：

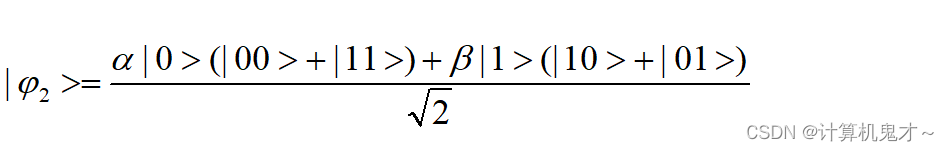
随即qubits[2]经过一个H门，得到| $\varphi _{3}$ >的状态：

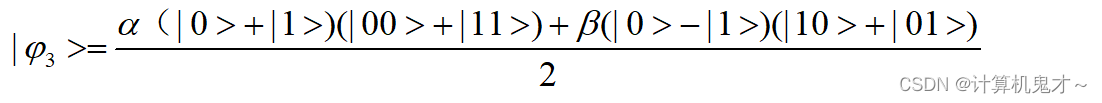
再进行一下小小的重组，可以把它改写为：

在测试代码时，我们调用函数，传入theta，由于最后使用了qvm.get_qstate()方法，得到了电路的量子态，所以理想结果会有四组：分别是当qubits[2],qubits[1]为|00>、|01>、|10>、|11>这四组结果。此时qubits[0]为|0>的幅值是 $\alpha$ ，为|1>的幅值是 $\beta$ 。

三、pyqpanda实现代码

def question2(theta: float) -> list:
    qvm = CPUQVM()
    qvm.init_qvm()
    qubits = qvm.qAlloc_many(3)

    cbits = qvm.cAlloc_many(3)
    # 构造量子程序prog
    prog = QProg()
    progx = QProg()
    progz = QProg()
    measureprog = QProg()

    progx.insert(X(qubits[0]))
    progz.insert(Z(qubits[0]))
    measureprog.insert(Measure(qubits[2], cbits[2]))
    measureprog.insert(Measure(qubits[1], cbits[1]))
    # 构造条件分支
    qifx = create_if_prog(cbits[1], progx)
    qifz = create_if_prog(cbits[2], progz)

    prog.insert(RY(qubits[2], theta))
    prog.insert(H(qubits[1]))
    prog.insert(CNOT(qubits[1], qubits[0]))
    prog.insert(CNOT(qubits[2], qubits[1]))
    prog.insert(H(qubits[2]))
    prog.insert(measureprog)
    # 先测量前面两个量子比特
    qvm.directly_run(prog)
    # 先X后Z
    prog.insert(qifx)
    prog.insert(qifz)

    RESULT = qvm.directly_run(prog)
    result2 = qvm.get_qstate()
    # 输出并返回列表
    print(result2)
    return result2