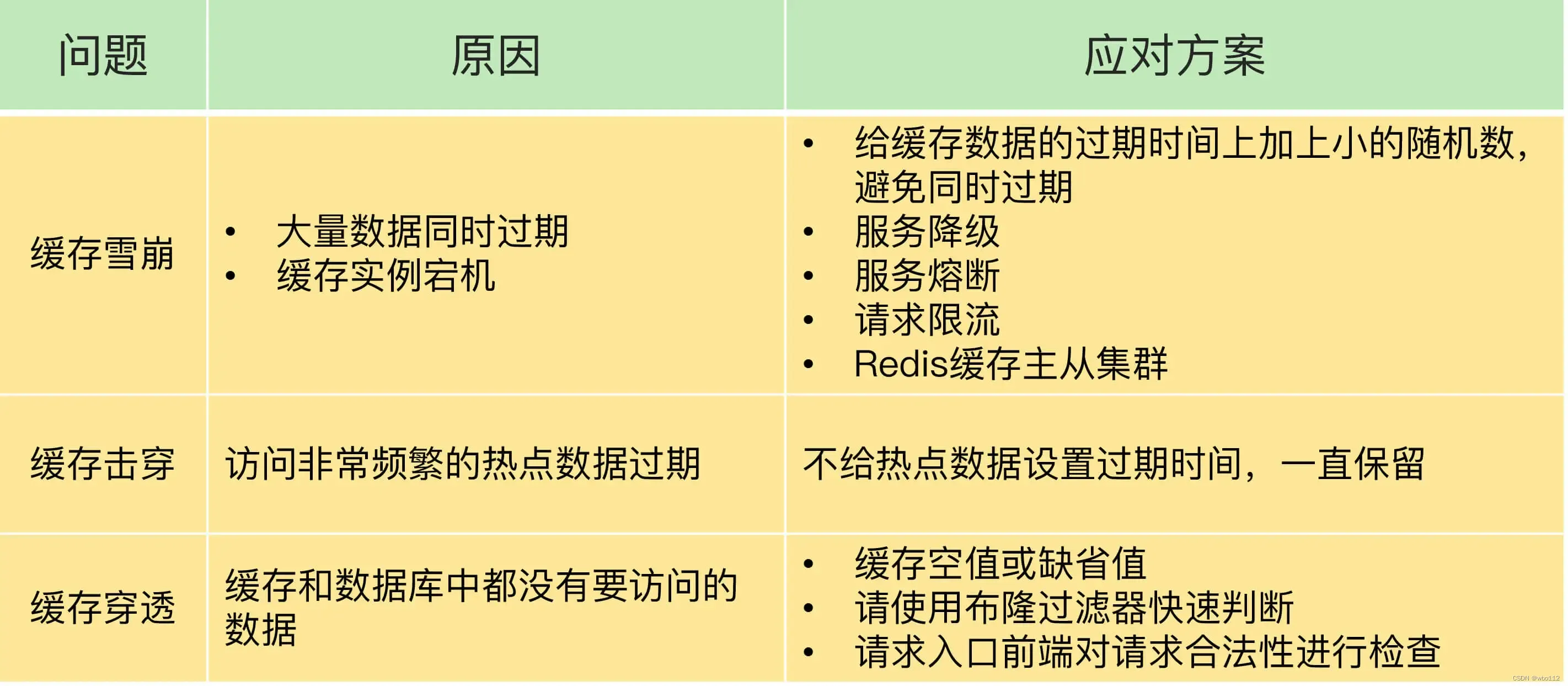
上一篇文章的曲线是由触摸点直接生成的，但触摸点并非连续的，而是离散的，而且屏幕触摸点采样的间隔时间其实不短，因此如果单纯只用触摸点生成OpenGL触摸曲线，在高速书写时会导致曲线看起来就像多个线段合起来一样（事实也是如此）。

        为了解决这个问题，最好的办法就是像Path一样使用Bezier曲线，以三次触摸坐标记录为关键点补间出相对更细密的曲线坐标，从而使线段变得更光滑。

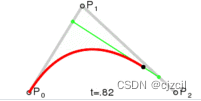
        二次贝塞尔曲线的原理：

        假定我现在有3个顶点（P0、P1、P2），想以曲线的方式进行绘制其路径，那么可以从P0到P1、P1到P2两个线段，按照同样的百分比步进量，沿着这两个线段对应百分比的位置连接为一个新的线段（图中绿色部分），然后取这个线段同样百分比位置的坐标，将这些坐标连城线即可得到一端曲线。

 

 

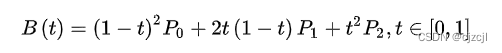
推导：

        但现在要面临的是不定数目的线条顶点，如何才能使用二次贝塞尔曲线连成一个光滑的曲线呢？

        首先像下图这样，画完一段曲线后，关键点全部顺移一个序号，肯定是无法收尾相接的，因为两个曲线段之间断开了：

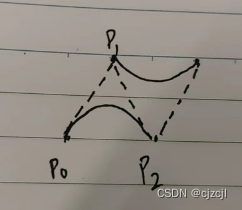
        克服办法也不难想到，每段线段起始的位置，都把上一次使用的P0和P1向量相加之后除以2，即可让下一段曲线的起始段和之前曲线的结尾段结合起来了。

        关键代码如下：

        二次贝塞尔关键点的计算：

PointF keyPoint0 = new PointF((mBezierKeyPoint0[0] + mBezierKeyPoint1[0]) / 2f, (mBezierKeyPoint0[1] + mBezierKeyPoint1[1]) / 2f);
PointF keyPoint1 = new PointF(mBezierKeyPoint1[0], mBezierKeyPoint1[1]);
PointF keyPoint2 = new PointF((x + mBezierKeyPoint1[0]) / 2f, (y + mBezierKeyPoint1[1]) / 2f);
List<PointF> points = bezierCalc(new PointF[] {keyPoint0, keyPoint1, keyPoint2});

        二次贝塞尔曲线点计算方法：

private List<PointF> bezierCalc(PointF[] keyPointP) {
    List<PointF> points = new LinkedList<>();
    double t = 0.1f; //步进
    for (double k = 0; k <= 1f; k += t) {
        double r = 1 - k;
        double x = Math.pow(r, 2) * keyPointP[0].x + 2 * k * r * keyPointP[1].x
                + Math.pow(k, 2) * keyPointP[2].x;
        double y = Math.pow(r, 2) * keyPointP[0].y + 2 * k * r * keyPointP[1].y
                + Math.pow(k, 2) * keyPointP[2].y;
        points.add(new PointF((float) x, (float) y));
    }
    return points;
}

        再把上述算法插入到上次的GL线条绘制代码中，在生成线条顶点之前通过以上算法插值平滑一下，最后结果如下：