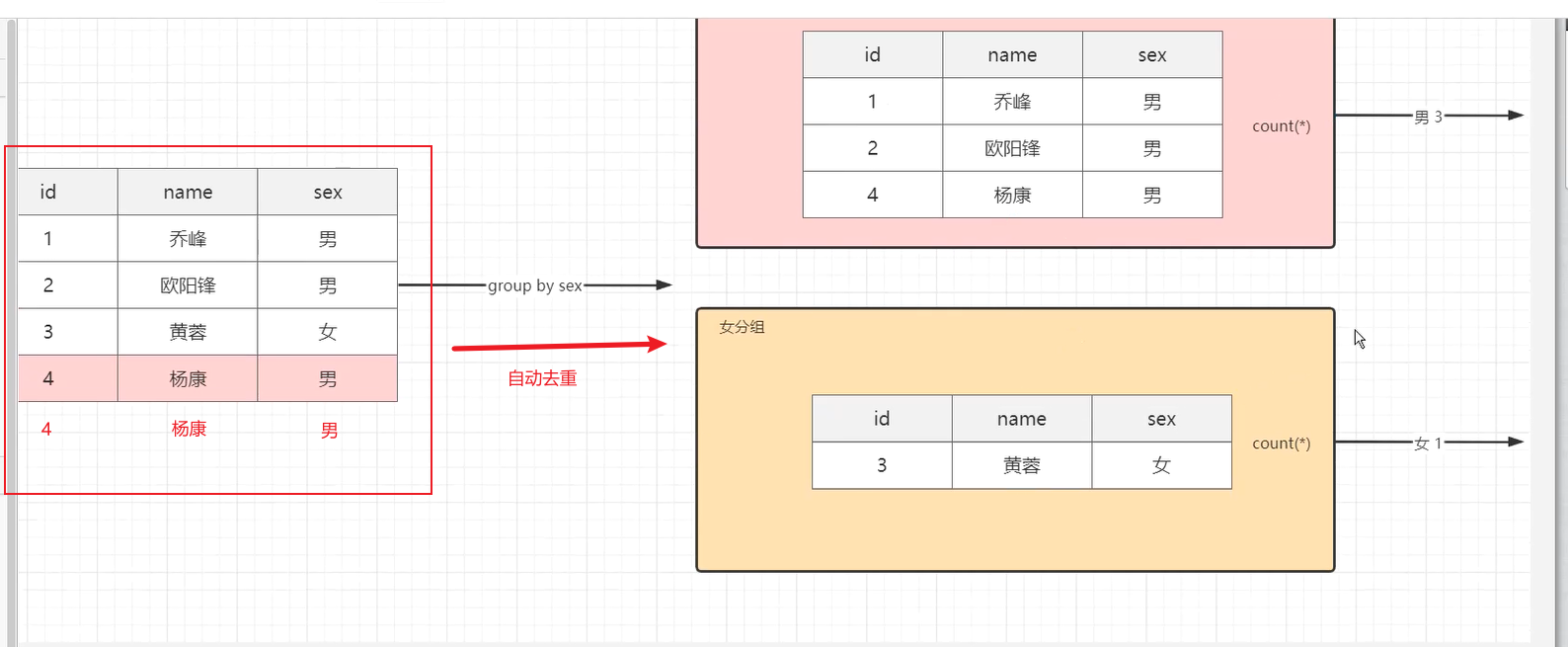
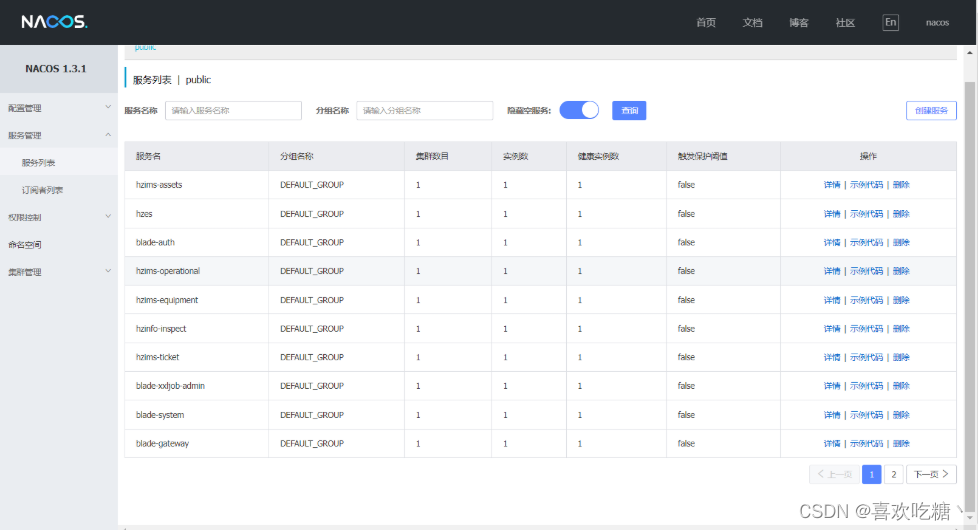
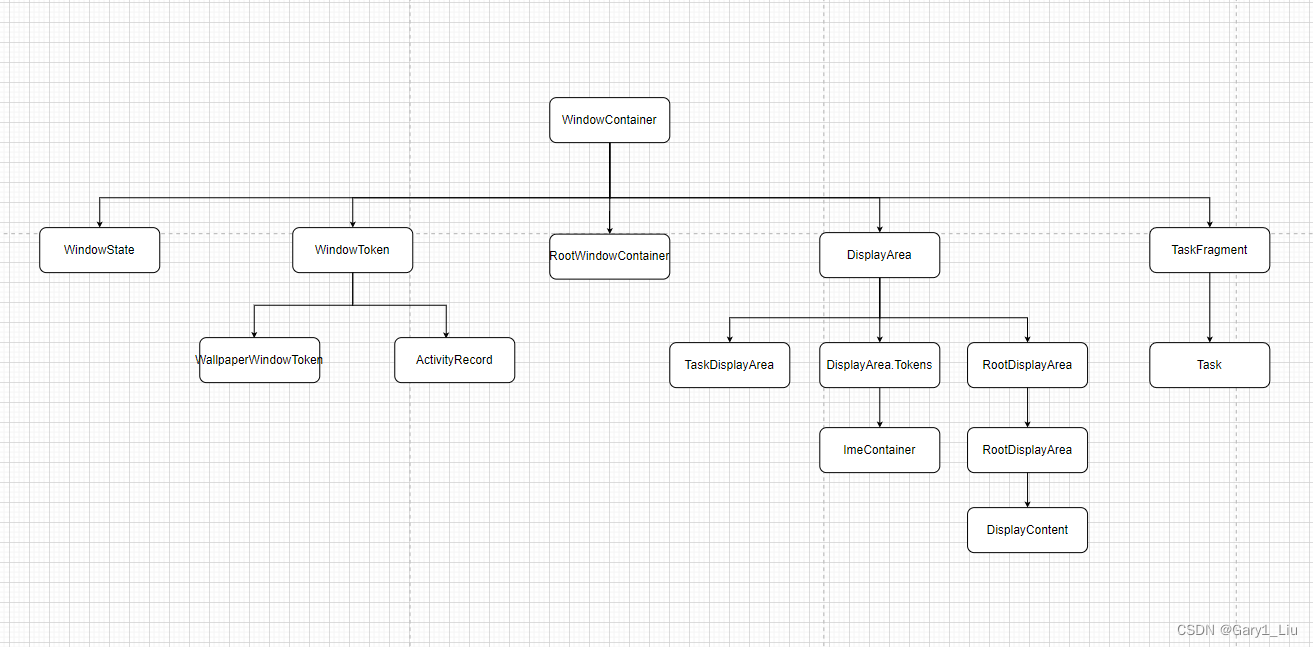
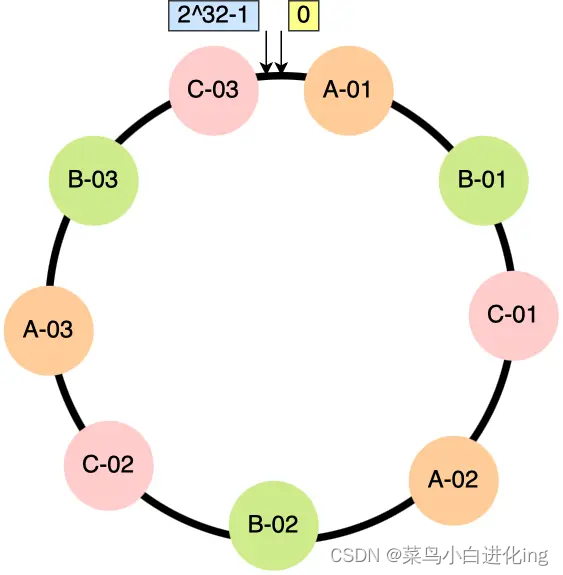
求倒数的算法

两个数互为倒数，是说这两个数乘起来等1.比如a和b互为倒数，那么ab=1.

5的倒数是0.2，我们可以很简单的求出来，但是如何在密文域中求一个数的倒数呢？

文章《An investigation of complex operations with word-size homomorphic encryption》中给出了一个算法。

我们假设y=1-x，y的模小于（对于实数来说，就是绝对值）0.5，那么有下面的式子成立

$x(1+y)(1+y^2)(1+y^{2^2}) \cdots (1+y^{2^{r-1}})=1-y^{2^{r}}$

将x=1-y代入，用平方差公式，可以快速证明。

当r足够大的时候，显然，上述式子就为1，我们要求的x的倒数，就可以通过左边的式子来求

$\frac{1}{x}=(1+y)(1+y^2)(1+y^{2^2}) \cdots$

这样，我们就得到了一个迭代法，可以只用加法和乘法来计算一个数的倒数。

但是，上面的方法可能有一点问题，也就是这时候的x只能是[0.5,1]这个范围，而且，参与计算的y是小数。

我们将上面的式子左右两边同时乘以一个 $p^{2^r}$ ，令z=xp，y=p-z那么有

$z(p+y)(p^2+y^2)(p^{2^2}+y^{2^2})\cdots (p^{2^{r-1}}+y^{2^{r-1}})=p^{2^r}-y^{2^r}$

这样就可以计算当y的模小于p/2了。

不过，显然，当p=1的时候，计算量会小很多

TenSEAL使用CKKS代码示例

import tenseal as ts
ctx=ts.context(ts.SCHEME_TYPE.CKKS, poly_modulus_degree=8192, coeff_mod_bit_sizes=[44,30,30,30,30,44])
ctx.global_scale=2**30
import numpy as np 
m1=np.array([1.2,0.6,0.4])
c0=ts.ckks_vector(ctx,m1)
p1=1
p=p1
r=4
t=p-c0
c=t
v=p+c
for i in range(r-1):
    c=c*c
    p=p*p
    v=v*(p+c)
m=v.decrypt()
m=np.array(m)/(p1**(2**(r)))

print(m)

print(m*m1)

当r=2或者3的时候，跑出来的结果就已经比较准确了

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/503306.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！