MLP神经网络的结构和原理

神经网络其实是对生物神经元的模拟和简化，生物神经元由树突、细胞体、轴突等部分组成。
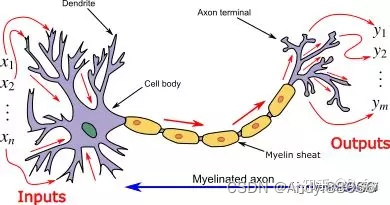生物神经元具有兴奋和抑制两种状态，当接受的刺激高于一定阈值时，则会进入兴奋状态并将神经冲动由轴突传出，反之则没有神经冲动。

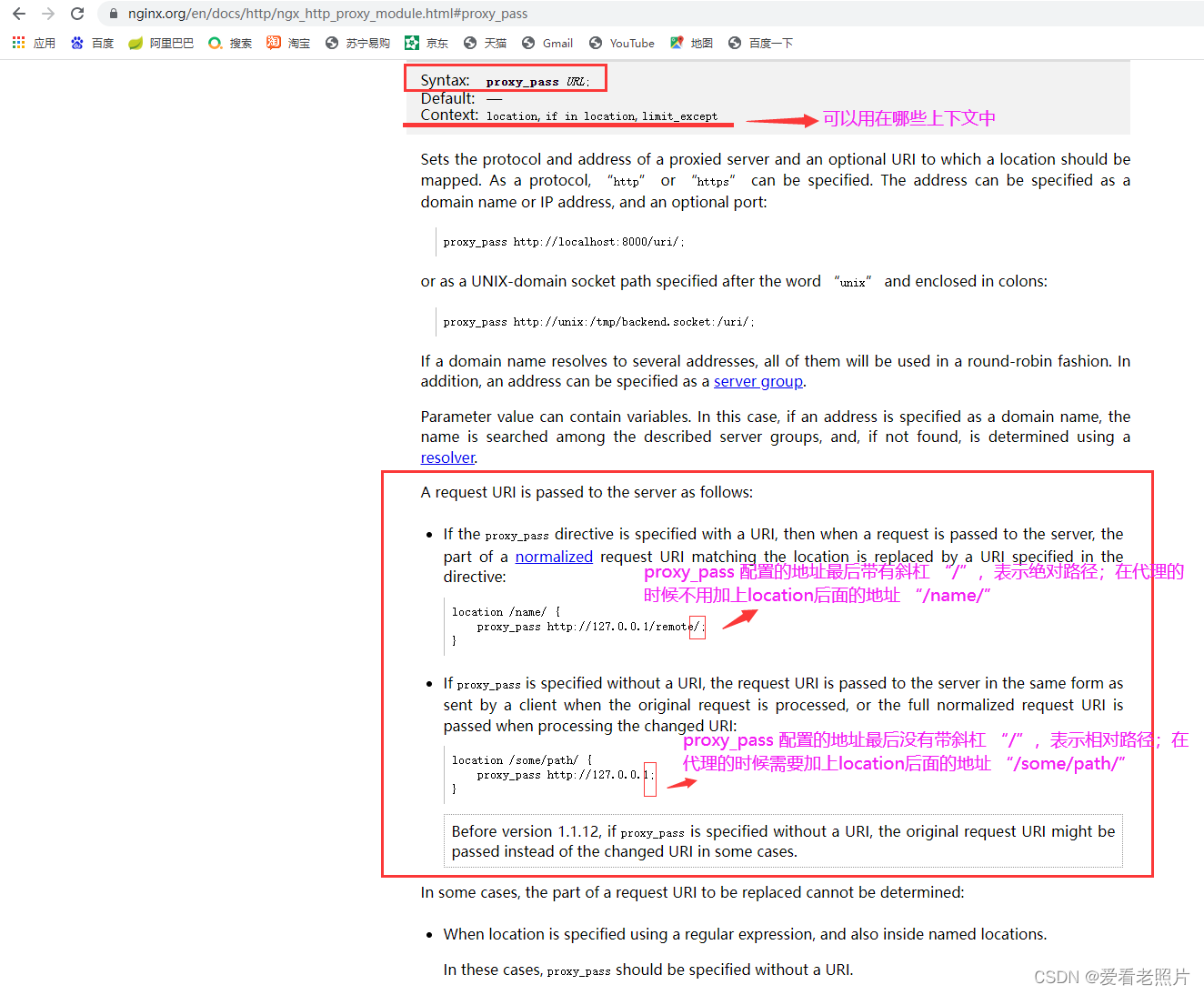
我们基于生物神经元模型可得到多层感知器MLP的基本结构，最典型的MLP包括包括三层：输入层、隐层和输出层，MLP神经网络不同层之间是全连接的（全连接的意思就是：上一层的任何一个神经元与下一层的所有神经元都有连接。
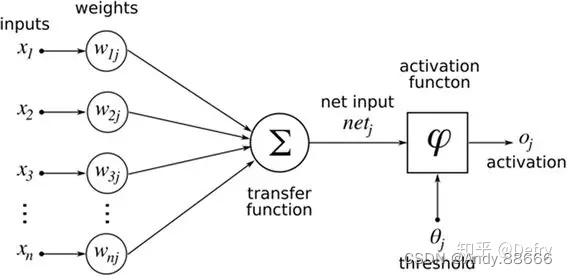由此可知，神经网络主要有三个基本要素：权重、偏置和激活函数

权重：神经元之间的连接强度由权重表示，权重的大小表示可能性的大小

偏置：偏置的设置是为了正确分类样本，是模型中一个重要的参数，即保证通过输入算出的输出值不能随便激活。

激活函数：起非线性映射的作用，其可将神经元的输出幅度限制在一定范围内，一般限制在（-1_1）或（01）之间。最常用的激活函数是Sigmoid函数，其可将（-∞，+∞）的数映射到（0~1）的范围内。

MLP的最经典例子就是数字识别，即我们随便给出一张上面写有数字的图片并作为输入，由它最终给出图片上的数字到底是几

对于一张写有数字的图片，我们可将其分解为由28*28=784个像素点构成，每个像素点的值在（0~1）之间，其表示灰度值，值越大该像素点则越亮，越低则越暗，以此表达图片上的数字并将这786个像素点作为神经网络的输入。

隐层的层数和神经元的选择需根据具体情况选择，此例选择两层隐层，每层16个神经元。那么根据上面的叙述，根据权重、偏置的个数此神经网络将会有13002个参数需要去调节，而如何调整这些参数，从而使神经网络有较好的学习效果则正是下篇更新的神经网络训练和学习的内容。

通过楼主上面的叙述，该图像识别问题最终可通过线性方程的方式表示出来，从而来描述本篇通过MLP神经网络进行数字识别的案例，并通过建立的问题描述模型来编程实现。