例题一

$$\sum _{i=1}^n\lfloor \frac{n}{i}\rfloor$$

首先很容易想到直接求解，对于较大的数据，$O(n)$做法无法通过。

注意到函数$y=\lfloor \frac{n}{x}\rfloor$的图像如下：

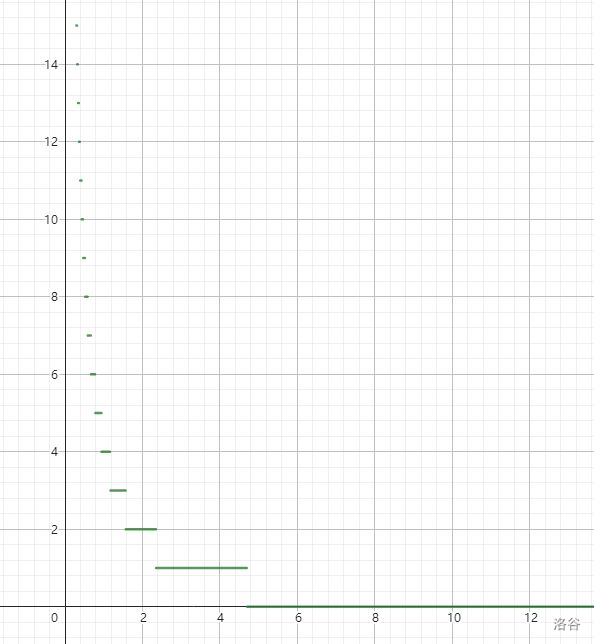
不难发现，随着 $x$ 增大 ，$y$单调不增，这说明对于相同值的 $y$ 总是分布在同一块区域。

这启发我们根据$y$值，把$x$分组，每组“打包”算好。

这个时间复杂度显然是 $O(\sqrt{n})$的，时间复杂度与$\lfloor \frac{n}{x}\rfloor$的数量有关，这个数量大概是$2\sqrt{n}$。

虽然图像上看$y$的数量很大，但是考虑到许多$y$不包含整数的$x$,因此时间复杂度就是这样的了。

代码实现如下：

for(LL l=1,r;l<=n;l=r+1)
{
   r=n/(n/l);
   ans+=(n/l)*(r-l+1);
}

例题二

$$\sum _{i=1}^{n}k\mathrm{mod}i$$

对原式进行推导：

$$\begin{gathered} \sum _{i=1}^{n}k\mathrm{mod}i \\ =\sum _{i=1}^{n}k-i\lfloor \frac{k}{i}\rfloor \\ =nk-\sum _{i=1}^{n}i\lfloor \frac{k}{i}\rfloor \end{gathered}$$

后面的部分可以用整除分块解决，对于每个$\lfloor \frac{n}{i}\rfloor$,内部相当于一个等差数列。

代码实现如下：

ans=n*k;
for(LL l=1,r;l<=n&&l<=k;l=r+1)
{
    r=min(k/(k/l),n);
    ans-=(k/l)*(r+l)*(r-l+1)/2;
}

例题三

函数 $f(i)$ 表示 $i$ 所有约数的和。

求 $\sum _{i=L}^{R}f(i)$。

考虑前缀和作差，问题变成$[1,R]-[1,L-1]$。

于是不难列出式子求解，与上一题很像。

例题四

$$\sum _{i=1}^n\sum _{j=1}^m(n\mathrm{mod}i)(m\mathrm{mod}j)$$

这道题显然也是推导。

$$\begin{gathered} \sum _{i=1}^n\sum _{j=1}^m(n\mathrm{mod}i)(m\mathrm{mod}i) \\ =\sum _{i=1}^n(n\mathrm{mod}i)\sum _{j=1}^m(m\mathrm{mod}j) \\ =\sum _{i=1}^n(n-i\lfloor \frac{n}{i}\rfloor )\sum _{j=1}^m(m-j\lfloor \frac{m}{j}\rfloor ) \\ =(n^2-\sum _{i=1}^{n}i\lfloor \frac{n}{i}\rfloor )(m^2-\sum _{j=1}^{m}m\lfloor \frac{m}{j}\rfloor ) \end{gathered}$$

左右两边分开计算即可。

例题五

$$\sum _{i=1}^n(n\mathrm{mod}i)(m\mathrm{mod}i)$$

和上道题看着很像，不过这道题就很复杂了。

$$\begin{gathered} \sum _{i=1}^n(n\mathrm{mod}i)(m\mathrm{mod}i) \\ =\sum _{i=1}^n(n-i\lfloor \frac{n}{i}\rfloor )(m-i\lfloor \frac{m}{i}\rfloor ) \\ =\sum _{i=1}^n(nm-(n+m)i\lfloor \frac{n}{i}\rfloor +i^2\lfloor \frac{n}{i}\rfloor \lfloor \frac{m}{i}\rfloor ) \\ =n^{2}m-(n+m)\sum _{i=1}^{n}i\lfloor \frac{n}{i}\rfloor +\sum _{i=1}^n{i}^2\lfloor \frac{n}{i}\rfloor \lfloor \frac{m}{i}\rfloor \end{gathered}$$

前面的式子我们已经可以轻松求出了，对于后面的这个东西，我们还是画图观察：

显而易见，仍然满足我们刚开始的两个性质，因此依旧使用之前的方式进行整除分块，时间复杂度依旧是$O(\sqrt{n})$。

具体思想如下：

我们的值变化，要么是因为 $\lfloor \frac{n}{x}\rfloor$ 变化了，要么是因为 $\lfloor \frac{m}{x}\rfloor$ 变化了。

因此找出 $\lfloor \frac{n}{x}\rfloor$ 变化的点和 $\lfloor \frac{m}{x}\rfloor$ 变化的点中最近的一个，作为我们的 $r$ 值。

后面部分的代码实现如下：

for(LL l=1,r=0;l<=n;l=r+1)
{
    r=min(n/(n/l),m/(m/l));
    ans=ans+(n/l)*(m/l)*(sum(r)-sum(l-1));
}

这里出现了一个函数，它的作用是求出：$su{m}_i=\sum _{i=1}^n{i}^2$。

公式是 $\sum _{i=1}^n{i}^2=\frac{n(n+1)\times (2n+1)}{6}$，用数学归纳法很好证明，这里不多赘述了。