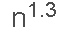392.判断子序列

本题可以直接用双指针解法。但是本题是编辑距离的入门题目，故采用动态规划解法为后序“编辑距离”类题目打基础。
本题与最大子序列非常相似，但不同的是s必须连续，t可以不连续。
五部曲
1、dp[i][j]
表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。
2、递推公式
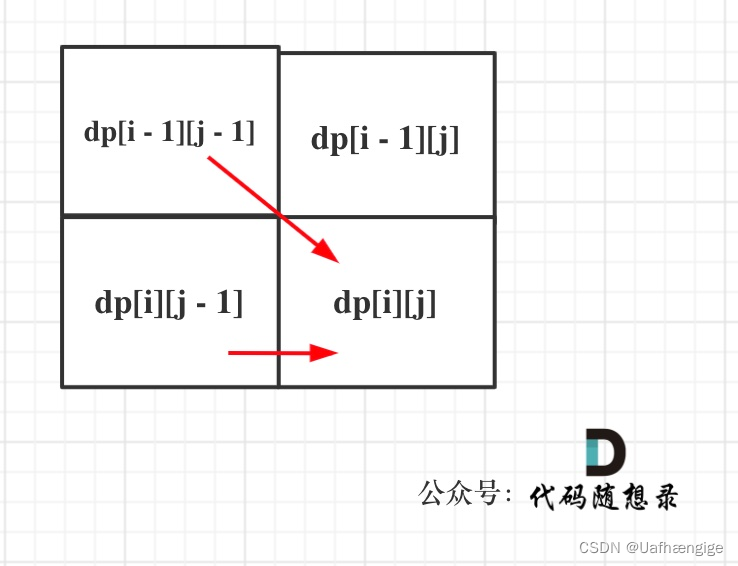
if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
else dp[i][j] = dp[i][j-1]
3、初始化
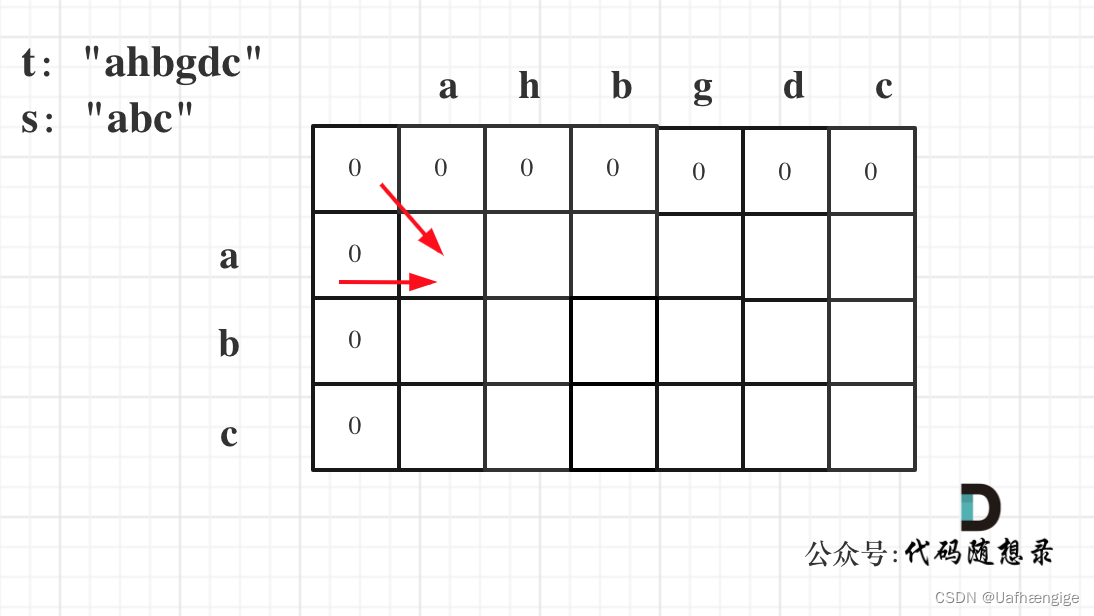
在定义dp[i][j]含义的时候为什么要表示以下标i-1为结尾的字符串s，和以下标j-1为结尾的字符串t，相同子序列的长度为dp[i][j]。

因为这样的定义在dp二维矩阵中可以留出初始化的区间，如图：
4、遍历顺序

class Solution {
public:
    bool isSubsequence(string s, string t) {
        if(s.length() > t.length()) return false;
        vector<vector<int>> dp(s.size()+1,vector<int>(t.size()+1,0));
        for(int i = 1; i <= s.size();++i){
            for(int j = 1; j <= t.size();++j ){
                if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + 1;
                else dp[i][j] = dp[i][j-1];
            }
        }
        return dp[s.size()][t.size()] == s.size();
    }
};

115.不同的子序列

3、初始化
每次当初始化的时候，都要回顾一下dp[i][j]的定义，不要凭感觉初始化。

dp[i][0]表示什么呢？

dp[i][0] 表示：以i-1为结尾的s可以随便删除元素，出现空字符串的个数。

那么dp[i][0]一定都是1，因为也就是把以i-1为结尾的s，删除所有元素，出现空字符串的个数就是1。

再来看dp[0][j]，dp[0][j]：空字符串s可以随便删除元素，出现以j-1为结尾的字符串t的个数。

那么dp[0][j]一定都是0，s如论如何也变成不了t。

最后就要看一个特殊位置了，即：dp[0][0] 应该是多少。

dp[0][0]应该是1，空字符串s，可以删除0个元素，变成空字符串t。

class Solution {
public:
    int numDistinct(string s, string t) {
        vector<vector<uint64_t>> dp(s.size()+1,vector<uint64_t>(t.size()+1,0));
        for(int i = 0; i <= s.size();++i) dp[i][0] = 1;

        for(int i = 1; i<=s.size();++i){
            for(int j = 1; j<= t.size();++j){
                if(s[i-1] == t[j-1]) dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
                else dp[i][j] = dp[i-1][j];
            }
        }
        return dp[s.size()][t.size()];
    }
};