一.背景 

       1859年，当一位叫托马斯·奥斯汀的农民收到英国老家送来的24只野兔并将它们放归农场的时候，他绝对意想不到，这些看似人畜无害的小兔子，竟为古老的澳洲大陆带来一场巨大的生态破坏。到20世纪初，澳大利亚的兔子数量已经多到了灾难的程度。它们与本土动物争夺栖息地，造成了小型有袋动物的大量减少。它们环剥树皮，啃食庄稼，密集的兔洞穿空土地带来严重的水土流失。兔子们以每年80英里的速度在澳大利亚境内迁徙，从最初的落脚地维多利亚，进入新南威尔士、南澳大利亚、昆士兰，直至西澳大利亚。时至今日，依然有2亿至3亿只欧洲野兔生活在澳大利亚。

二.斐波那契数列

       如果说,兔子在出生两个月之后,就拥有繁殖能力,一对兔子每个月能生出一对小兔子来,假设所有兔子都不死,那么一年之后可以繁殖多少对兔子呢?

       我们拿新出生的一对小兔子分析一下：第一个月小兔子没有繁殖能力，所以还是一对；两个月后，生下一对小兔子数共有两对；三个月以后，老兔子又生下一对，因为小兔子还没有繁殖能力，所以一共是三对……依次类推可以列出下表:

所经过的月数	1	2	3	4	5	6	7	8	9	10	11	12
兔子对数	1	1	2	3	5	8	13	21	34	55	89	144

 

表中数字1,1,2,3,5,8......构成了一个序列.这个这个数列有个十分明显的特点，那是：前面相邻两项之和，构成了后一项.

 

我们用数学函数来定义就是:

 

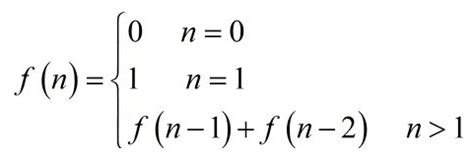
 用代码怎么实现呢?

int Fbi(int n)
{
	if(n==1||n==2)//通过数列的规律发现,前两项都为1,作为递归的终止条件
	{
		return 1;
	}
	else
	{
		return Fbi(n-1)+Fbi(n-2);//要求第n项,就是求n-1项和n-2项的和
	}
}
int main()
{
	int i,n;
	printf("请输入你要打印的斐波那契数列项数:\n");
	scanf("%d",&n);//n为打印的项数
	printf("斐波那契数列:");
	for(i=1;i<=n;i++)
	{
		printf("%d ",Fbi(i));//fun函数返回的是第i项，所以用for循环打印每一项
	}
	return 0;
}

我们来模拟代码中Fbi(i)函数中 i=5的执行过程,如图所示:

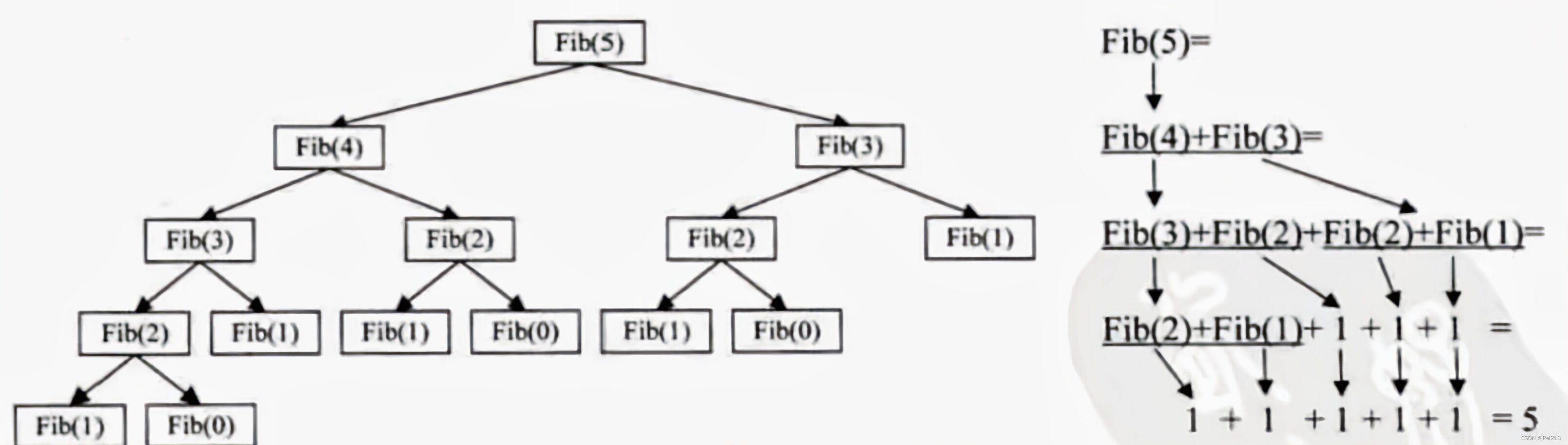
 三.递归

       在高级语言中，调用自己和其他函数并没有本质的不同。我们把一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称做递归函数。
       当然，写递归程序最怕的就是陷入永不结束的无穷递归中，所以，每个递归定义必须至少有一个条件，满足时递归不再进行，即不再引用自身而是返回值退出。比如刚才的例子，总有一次递归会使得i<2的，这样就可以执行return i的语句而不用继续递归了。
       大量的递归调用会建立函数的副本，会耗费大量的时间和内存。

四.栈

        那么我们所讲的递归,和栈有什么关系呢？这得从计算机系统的内部说起。

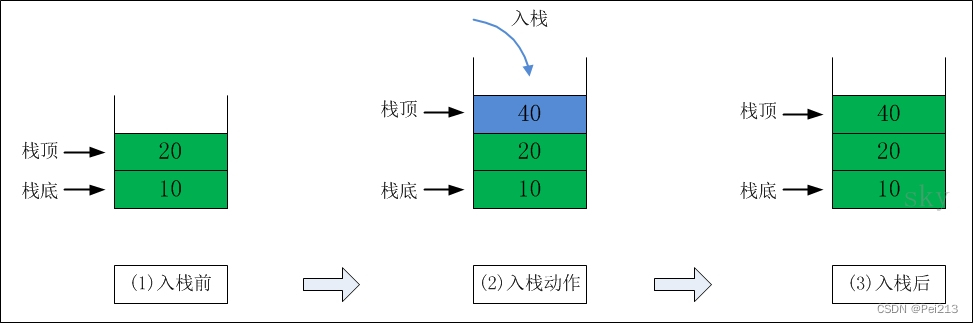
        前面我们已经看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序是它前行顺序的逆序。在退回过程中，可能要执行某些动作，包括恢复在前行过程中存储起来的某些数据。
这种存储某些数据，并在后面又以存储的逆序恢复这些数据，以提供之后使用的需求，显然很符合栈这样的数据结构，因此，编译器使用栈实现递归就没什么好惊讶的了。
        简单的说，就是在前行阶段，对于每一层递归，函数的局部变量、参数值以及返回地址都被压入栈中。在退回阶段，位于栈顶的局部变量、参数值和返回地址被弹出，用于返回调用层次中执行代码的其余部分，也就是恢复了调用的状态。
        当然，对于现在的高级语言，这样的递归问题是不需要用户来管理这个栈的，一切都由系统代劳了。