参考来源：
https://www.zhihu.com/question/323353814
本节主要围绕以下几个问题进行描述：
- 什么是FIR滤波器
- 时域的卷积=频域的相乘
关于FIR
FIR滤波就是在时域上卷积的过程。将含噪声信号与低通滤波器的傅里叶逆变换值进行卷积，这个过程就是FIR滤波。
任务描述
如下图，我们仿真生成了两段信号。其中一条是未加入噪声的纯净信号，另外一条是加入白噪声后的含噪声信号。其中纯净信号使用了一段正弦信号。我们的目的就是将含噪声信号中的噪声部分滤除，得到一条尽量还原纯净信号的滤波结果。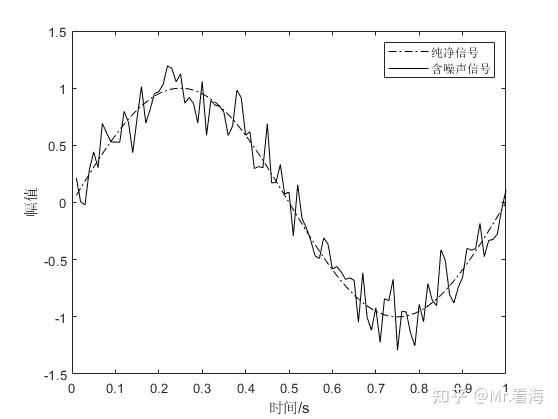
一种直观的方法
从上图容易看出，含噪声信号是在纯净信号上下波动的，所以很容易想到，如果取某几个含噪声信号的平均值，作为滤波结果，则可以抵消掉噪声在上下随机波动中的干扰效果。
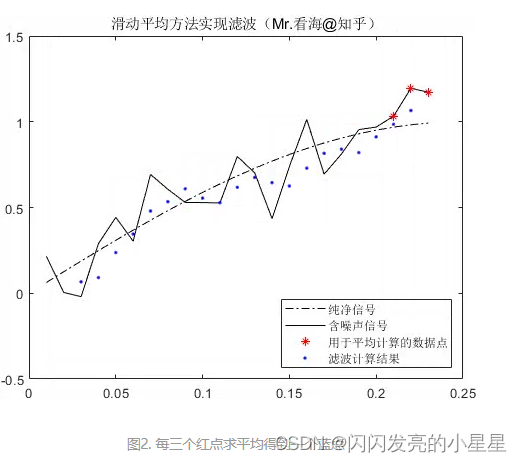
三、另外一种理解角度——引入权重系数概念
上边讲到的滑动平均，是将3个相邻信号求取平均值，这也可以理解为这3个值分别乘以权重系数1/3再求和，那么上述滤波过程可以用下边这张动图来演示，应该是比较直观的了：
图3. 选取了前10个数据点作为演示看到这里大家想到什么了吗。是的——是卷积。
卷积如何影响滤波算法的构造的？
卷积有一个重要性质：时域的卷积等于频域相乘。
这个性质可以说和滤波是息息相关的，因为滤波的目的就是想要得到某特定的频率段。
而频域相乘恰恰能够实现这个筛选的目的。
回到文章最开始的例子，想要对含噪声信号滤波，那我们不妨先看看他的频谱：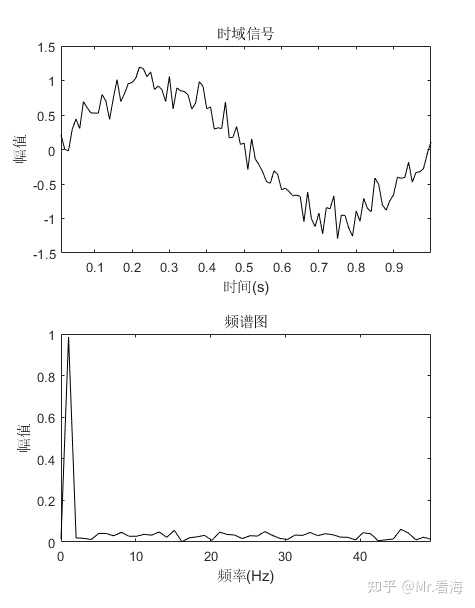
图11. 含噪声信号及其对应频谱可以看到我们想要保留的频率段范围基本在3Hz以下，高于3Hz的都可以抛弃，很自然地，我们可以想到一个办法，即构造如下一组频域信号：
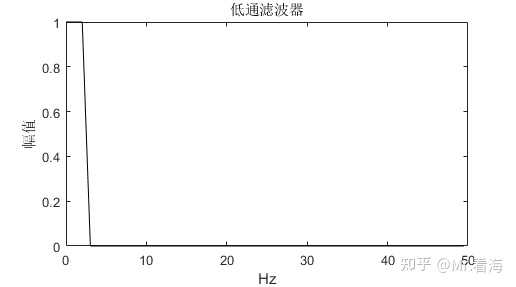图12. 构造的低通滤波器此时将图11中的频谱和图12相乘，高于3Hz的数值就全部变为了0，此时频谱就成了：
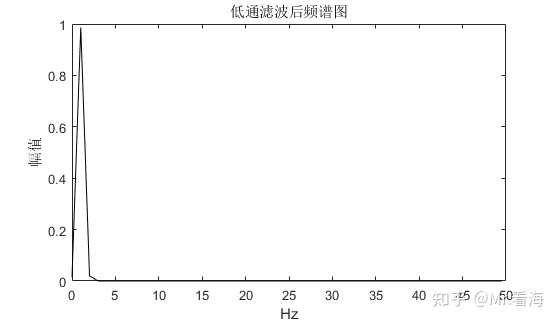图13. 高于3Hz的分量全部被滤除再将此频域数值进行傅里叶逆变换，得到时域数值：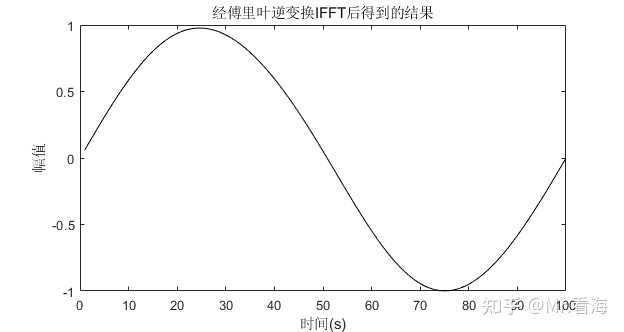
可以看到我们近乎完美的实现了滤波。一句话表述上述滤波过程：设计一个频域滤波器（将想要保留的频率段赋值为1，其他频率段赋值为0），将其与含噪声信号的频谱在频域上相乘，再将乘积做傅里叶逆变换，即可实现滤波，这种滤波器叫频域滤波器。
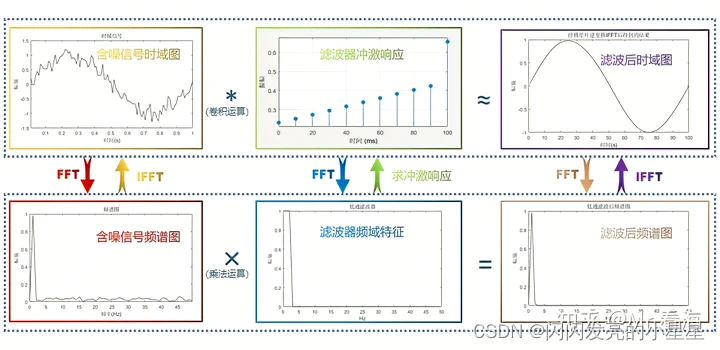
上面所说是在频域上相乘，时域的卷积=频域相乘!!!
所以，上述在频域空间的一大堆操作，可以简单地转化成在时域上的卷积操作，具体来说，就是将含噪声信号与低通滤波器的傅里叶逆变换值进行卷积，这个过程就是FIR滤波。
参考：
1. 如何通俗易懂地理解FIR/IIR滤波器？
2. matlab fir1
