1. 打家劫舍I

动态规划： dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 1) return nums[0];
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);
        for(int i = 2; i < nums.size(); ++i){
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[nums.size() - 1];
    }
};

2. 打家劫舍II

和打家劫舍I差不多，惟一的区别就是成环了。
所以考虑两种情况：

• 包含首元素，不包含尾元素
• 不包含首元素，包含尾元素

最后返回这两种情况中的最大值

class Solution {
public:
    int rob(vector<int>& nums) {
        // write code here
        if(nums.size() == 1) return nums[0];
        int result_start = rob(nums, 0, nums.size() - 2);
        int result_end = rob(nums, 1, nums.size() - 1);
        return max(result_start, result_end);
    }
    int rob(vector<int>& nums, int start, int end){
        if(end == start) return nums[start];
        vector<int> dp(nums.size(), 0);
        dp[start] = nums[start];
        dp[start + 1] = max(nums[start], nums[start + 1]);
        for(int i = start + 2; i <= end; ++i){
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
        }
        return dp[end];
    }
};

3. 打家劫舍III

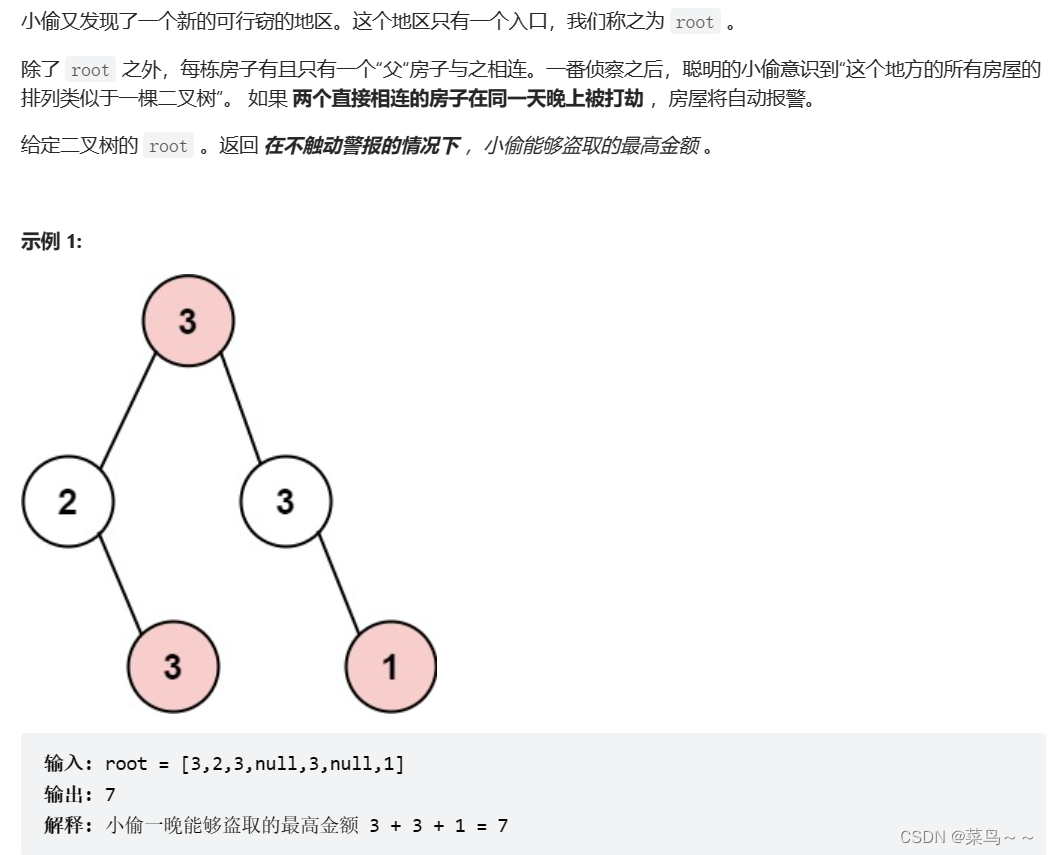
要做后序遍历，因为要通过递归函数的返回值来做下一步计算。

(1) 暴力递归超时

class Solution {
public:
    int rob(TreeNode* root) {
        if(root == nullptr) return 0;
        if(root->left == nullptr && root->right == nullptr) return root->val;

        int val1 = root->val;
        if(root->left) val1 += rob(root->left->left) + rob(root->left->right);
        if(root->right) val1 += rob(root->right->left) + rob(root->right->right);
        int val2 = rob(root->left) + rob(root->right);
        return max(val1, val2);
    }
};

(2) 记忆化搜索超时

class Solution {
public:
    int rob(TreeNode* root) {
        unordered_map<TreeNode*, int> umap;
        if(root == nullptr) return 0;
        if(root->left == nullptr && root->right == nullptr) return root->val;
        if(umap[root]) return umap[root];

        int val1 = root->val;
        if(root->left) val1 += rob(root->left->left) + rob(root->left->right);
        if(root->right) val1 += rob(root->right->left) + rob(root->right->right);
        int val2 = rob(root->left) + rob(root->right);
        umap[root] = max(val1, val2);
        return umap[root];
    }
};

(3) 动态规划

• 通过递归左节点，得到左节点偷与不偷的金钱。
• 通过递归右节点，得到右节点偷与不偷的金钱。
• 处理单层逻辑：如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]; 如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以val2 = max(left[0], left[1]) + max(right[0], right[1]);最后当前节点的状态就是{val2, val1};

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> res = robTree(root);
        return max(res[0], res[1]);
    }
    vector<int> robTree(TreeNode* root){
        if(root == nullptr) return {0, 0};
        vector<int> left = robTree(root->left);
        vector<int> right = robTree(root->right);
        //偷root
        int val1 = root->val + left[0] + right[0];
        //不偷root
        int val2 = max(left[0], left[1]) + max(right[0], right[1]);
        return {val2, val1};
    }
};