【机器学习实战】Python基于K均值K-means进行聚类（九）

news2024/11/19 3:38:25

文章目录

- 1 前言
- - 1.1 K-means的介绍
  - 1.2 K-means的应用
- 2 demo实战演示
- - 2.1 导入函数
  - 2.2 创建数据
  - 2.3 拟合聚类
  - 2.4 查看结果
- 3 使用高级技术评估集群性能*
- - 3.1 导入函数
  - 3.2 整合数据
  - 3.3 计算
- 4 讨论

1 前言

1.1 K-means的介绍

K均值（K-means）是一种基于距离度量的聚类算法，其主要思想是将数据集划分为k个不同的簇，每个簇代表一个相似度较高的数据组。该算法通过迭代优化来最小化所有数据点与其所属簇的欧氏距离之和，从而找到最佳的簇划分。

需要区分一下，K-means和KNN是两种不同的机器学习算法，K-means和KNN都是基于距离度量的算法，但前者用于聚类问题，而后者用于分类问题

K-means是一种聚类算法，它旨在将数据集分成k个不同的簇，每个簇代表一个相似度较高的数据组。该算法通过迭代优化来最小化所有数据点与其所属簇的欧氏距离之和，从而找到最佳的簇划分。
KNN（K-Nearest Neighbors）是一种分类算法，它将新样本与训练集中所有样本进行比较，并将其归为最接近的K个邻居中出现最多的类别。KNN算法使用欧氏距离或曼哈顿距离等计算相似性，然后根据K值确定邻居的数量。

优点：

简单易用：算法的实现十分简单，也容易理解。
可扩展性：在处理大规模数据时表现优秀，可以通过并行化等方法加速计算过程。
效率高：算法的迭代次数通常较少，因此计算速度很快。

缺点：

对初始值敏感：由于K-means算法是基于随机初始值进行迭代的，因此其结果很大程度上取决于初始中心点的选择。
容易陷入局部最优：容易陷入局部最优解，无法保证找到全局最优解。
簇数需要预先确定：需要预先确定簇的数量k，而实际应用中往往并不知道应该将数据划分成多少个簇。

1.2 K-means的应用

自然语言处理：K-means算法可用于文本聚类、主题建模和情感分析等自然语言处理任务。例如，将大量新闻文章聚类成不同的主题簇。
图像处理：K-means算法可用于图像分割、图像压缩和特征提取等图像处理任务。例如，使用K-means算法将图像像素分类为具有相似颜色和纹理的区域。
生物信息学：K-means算法可用于DNA序列和蛋白质序列的聚类和分类。例如，将蛋白质序列聚类到具有相似结构或功能的族群中。
金融风险管理：K-means算法可用于检测潜在的投资风险。例如，将投资组合分为不同的风险等级，并确定与每个等级相关的风险因素。
市场细分：K-means算法可用于市场细分和客户细分。例如，将消费者分成具有相似需求和偏好的不同类别，以便制定更有效的市场营销策略。
医疗诊断：K-means算法可用于分类和预测疾病。例如，将患有相似症状的患者分成具有类似病情的子组。

2 demo实战演示

2.1 导入函数

import matplotlib.pyplot as plt
from kneed import KneeLocator
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler

2.2 创建数据

#n_samples是要生成的样本总数，centers是要生成的中心数，cluster_std是标准偏差
features, true_labels = make_blobs(
     n_samples=200,
     centers=3,
     cluster_std=2.75,
     random_state=42
 )

查看数据

features[:5]

true_labels[:5]

缩放

scaler = StandardScaler()
scaled_features = scaler.fit_transform(features)
scaled_features[:5]

2.3 拟合聚类

kmeans = KMeans(
    init="random",
    n_clusters=3,
    n_init=10,
    max_iter=300,
    random_state=42
)
kmeans.fit(scaled_features)

2.4 查看结果

# 最低的SSE值
kmeans.inertia_

# 质心的最终位置
kmeans.cluster_centers_

# 收敛所需的迭代次数
kmeans.n_iter_

一般有两种常见的方法评估聚类数：

拐点法
轮廓系数

# 选择合适的簇，注意这里把n_clusters改了，运行多个值并且记录结果
kmeans_kwargs = {
    "init": "random",
    "n_init": 10,
    "max_iter": 300,
    "random_state": 42,
}

sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, **kmeans_kwargs)
    kmeans.fit(scaled_features)
    sse.append(kmeans.inertia_)

# 可视化
 plt.style.use("fivethirtyeight")
 plt.plot(range(1, 11), sse)
 plt.xticks(range(1, 11))
 plt.xlabel("Number of Clusters")
 plt.ylabel("SSE")
 plt.show()

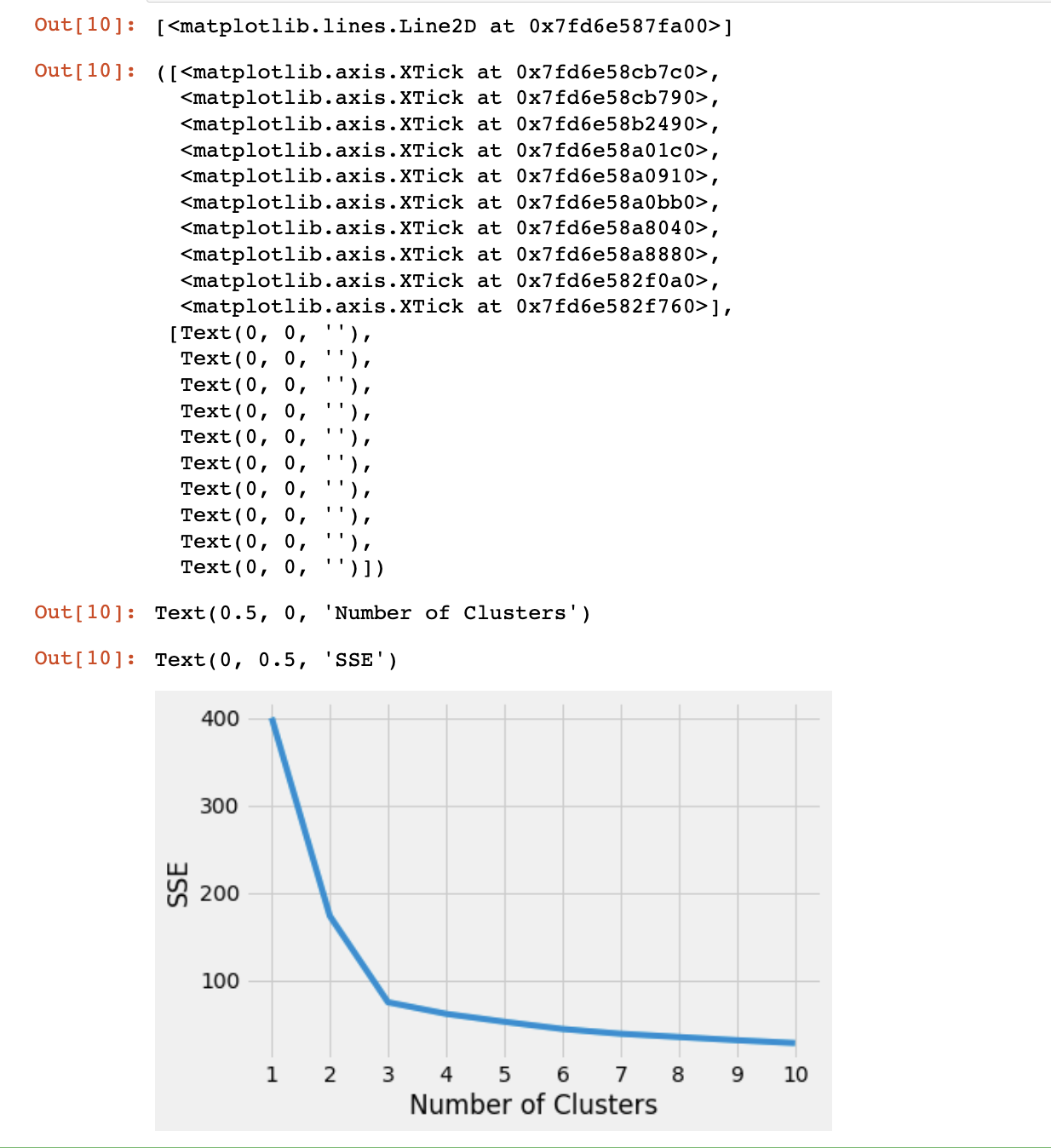
如图，这里很明显肉眼可见拐点是3，如果难以辨别可以通过kned识别

查看轮廓系数，轮廓系数是集群凝聚力和分离度的度量。它基于两个因素量化数据点与其分配的集群的匹配程度：轮廓系数值介于-1和之间1。较大的数字表示样本离它们的集群比离其他集群更近。

silhouette_coefficients = []

# 从轮廓系数的第2个集群开始
for k in range(2, 11):
    kmeans = KMeans(n_clusters=k, **kmeans_kwargs)
    kmeans.fit(scaled_features)
    score = silhouette_score(scaled_features, kmeans.labels_)
    silhouette_coefficients.append(score)
    
# 选最高分k值
plt.style.use("fivethirtyeight")
plt.plot(range(2, 11), silhouette_coefficients)
plt.xticks(range(2, 11))
plt.xlabel("Number of Clusters")
plt.ylabel("Silhouette Coefficient")
plt.show()

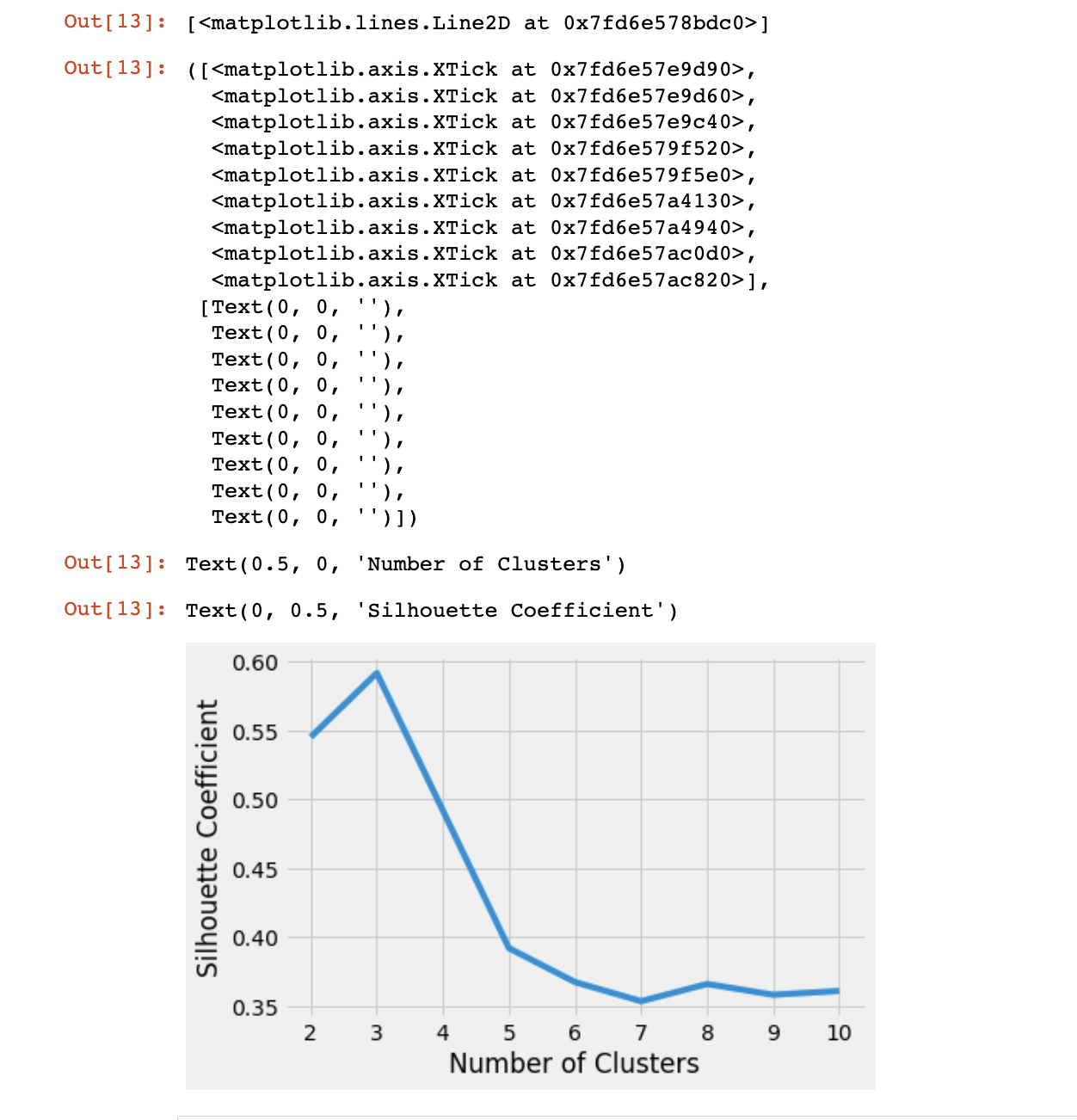
根据结果取最高分的点，这里依然是3

3 使用高级技术评估集群性能*

为了应付数据导致失真的情况，这是除了拐点法和轮廓系数外的一种高级方法

3.1 导入函数

from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
from sklearn.metrics import adjusted_rand_score

3.2 整合数据

函数如其名，整合成新月数据

features, true_labels = make_moons(
    n_samples=250, noise=0.05, random_state=42
)
scaled_features = scaler.fit_transform(features)

3.3 计算

分别用k均值算法和DBSCAN算法进行计算对比，

# Instantiate k-means and dbscan algorithms
kmeans = KMeans(n_clusters=2)
dbscan = DBSCAN(eps=0.3)

# Fit the algorithms to the features
kmeans.fit(scaled_features)
dbscan.fit(scaled_features)

# Compute the silhouette scores for each algorithm
kmeans_silhouette = silhouette_score(
    scaled_features, kmeans.labels_
).round(2)
dbscan_silhouette = silhouette_score(
   scaled_features, dbscan.labels_
).round (2)

kmeans_silhouette

dbscan_silhouette

可视化结果：

# 绘制数据和集群轮廓比较
fig, (ax1, ax2) = plt.subplots(
    1, 2, figsize=(8, 6), sharex=True, sharey=True
)
fig.suptitle(f"Clustering Algorithm Comparison: Crescents", fontsize=16)
fte_colors = {
    0: "#008fd5",
    1: "#fc4f30",
}
# k-means
km_colors = [fte_colors[label] for label in kmeans.labels_]
ax1.scatter(scaled_features[:, 0], scaled_features[:, 1], c=km_colors)
ax1.set_title(
    f"k-means\nSilhouette: {kmeans_silhouette}", fontdict={"fontsize": 12}
)

# dbscan
db_colors = [fte_colors[label] for label in dbscan.labels_]
ax2.scatter(scaled_features[:, 0], scaled_features[:, 1], c=db_colors)
ax2.set_title(
    f"DBSCAN\nSilhouette: {dbscan_silhouette}", fontdict={"fontsize": 12}
)
plt.show()

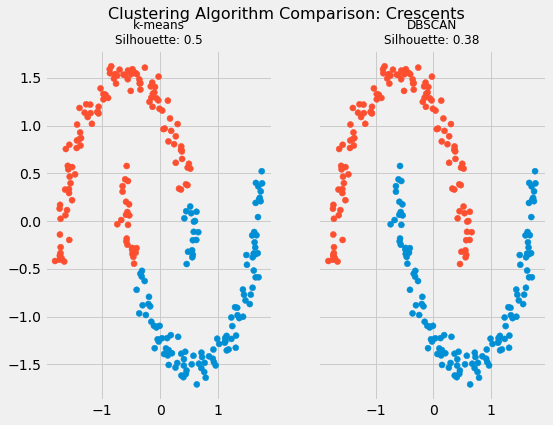
也可以参考调整兰特指数 (ARI，adjusted rand index)，ARI一般介于-1到1之间，越接近0表示分布的越随机，越接近1或-1表示可能存在误导性。

ari_kmeans = adjusted_rand_score(true_labels, kmeans.labels_)
ari_dbscan = adjusted_rand_score(true_labels, dbscan.labels_)

round(ari_kmeans, 2)

round(ari_dbscan, 2)