一、搜索二叉树的性质

二、搜索二叉树的结构定义

三、手撕搜索二叉树非递归

1）Insert()

2）Find()

3）Erase()

4）InOder()

5）BSTree(const BSTree& t) 拷贝构造

6）~BSTree()析构函数

四、手撕搜索二叉树递归

1）InsertR()

2）FindR()

3）EraseR()

五、搜索二叉树完整代码

一、搜索二叉树的性质

左子树上所有的节点的值都小于根节点的值
右子树上所有节点的值都大于根节点的值
它的左右子树分别为二叉搜索树

二、搜索二叉树的结构定义

搜索二叉树主要实现的是K或K/Value模型，这里我们使用K模型来定义，即可以用O(N)的时间复杂度来进行K值的搜索。

使用模板来定义

template<class K>
struct BSTreeNode
{
	BSTreeNode<K>* _left;
	BSTreeNode<K>* _right;
	K _key;

	BSTreeNode(const K& key)
		:_left(nullptr)
		,_right(nullptr)
		,_key(key)
	{

	}
};

三、手撕搜索二叉树非递归

1）Insert()

插入有两种情况：

_root == nullptr 根节点等于空

直接new a Node插入即可

if (_root == nullptr)
{
	_root = new Node(key);
	return true;
}

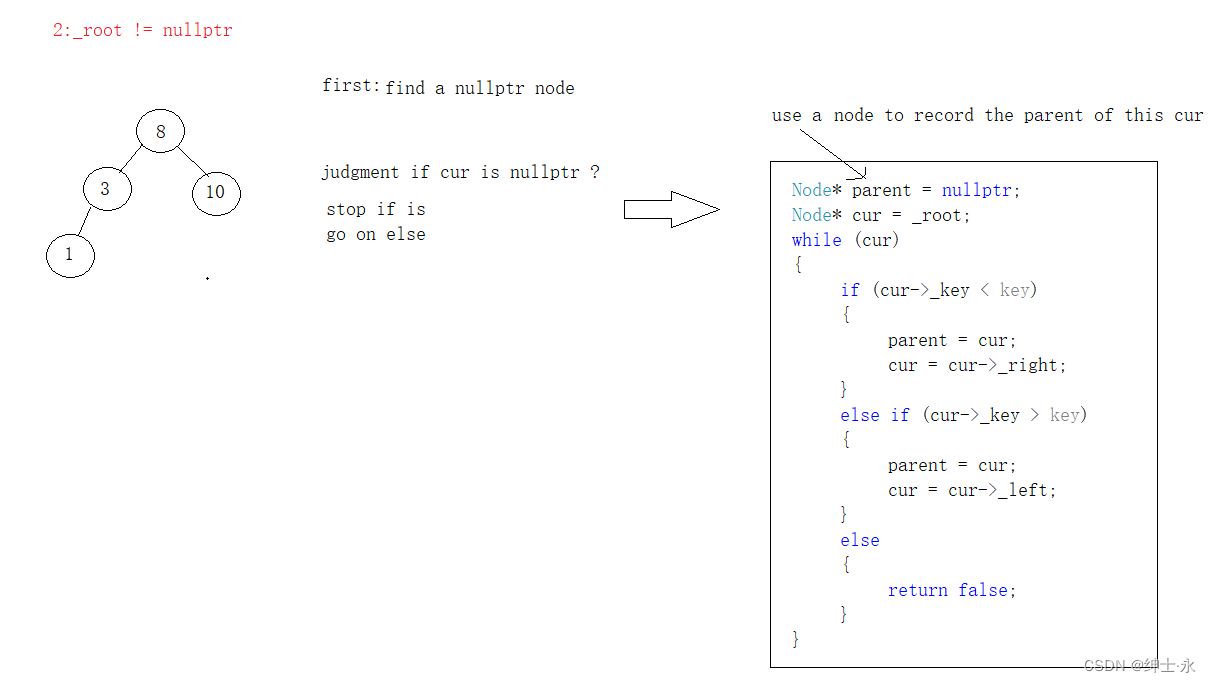
_root != nullptr 根节点不等于空

我们需要找到适合key值的空节点位置，通过搜索二叉树的性质进行排查位置

			Node* parent = nullptr;
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key < key)
				{
					parent = cur;
					cur = cur->_right;
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					return false;
				}
			}

			//开始插入
			cur = new Node(key);
			if (parent->_key < key)
			{
				parent->_right = cur;
			}
			else
			{
				parent->_left = cur;
			}

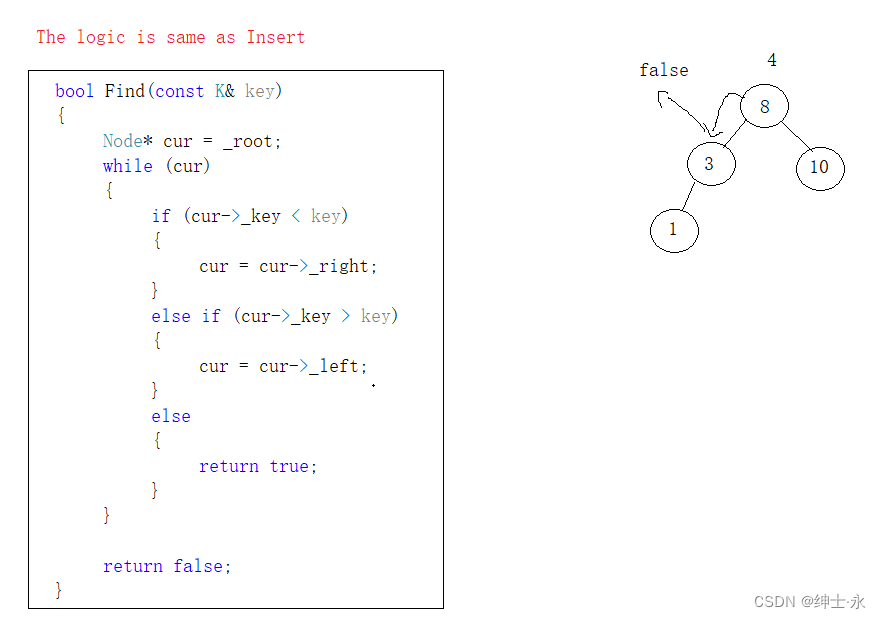
2）Find()

直接通过搜索二叉树的性质就可以进行查找，当key值大于cur->_key的值时，就查找cur的右子树，key值小于cur->_key的值时，就查找cur的左子树，直到找到，或者找不到cur == nullptr结束，即逻辑和Inser中的逻辑大同小异；

bool Find(const K& key)
{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				cur = cur->_left;
			}
			else
			{
				return true;
			}
		}
}

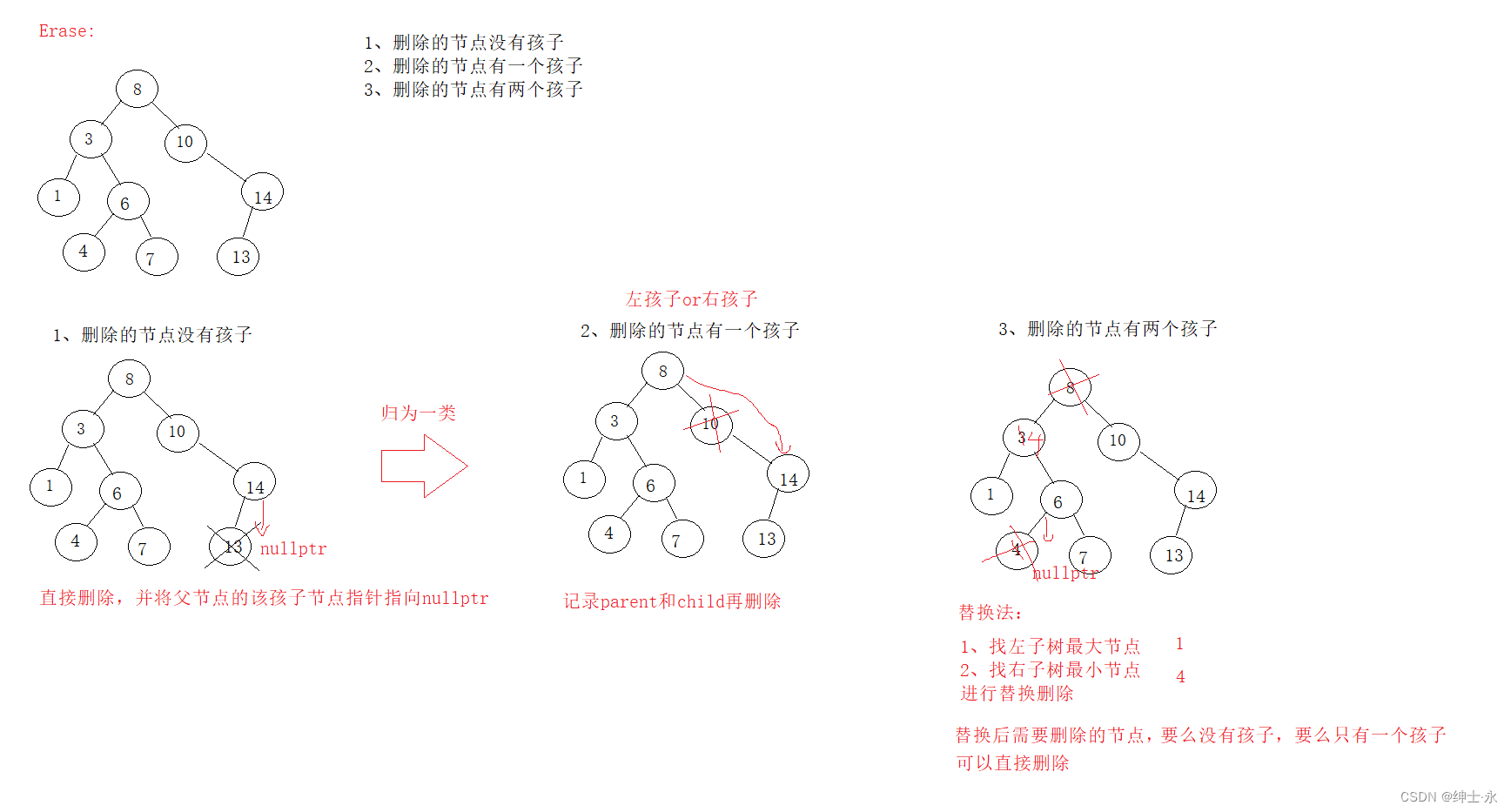
3）Erase()

删除分三种情况：

删除节点没有孩子
删除节点有一个孩子

有一个左孩子
有一个右孩子

删除节点有两个孩子

前面两种代码可以合并处理

	bool Erase(const K& key)
	{
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (cur->_key < key)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (cur->_key > key)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//开始删除
				if (cur->_left == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_right;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_right;
						}
						else
						{
							parent->_right = cur->_right;
						}
					}

					delete cur;
					cur = nullptr;
				}
				else if (cur->_right == nullptr)
				{
					if (cur == _root)
					{
						_root = cur->_left;
					}
					else
					{
						if (cur == parent->_left)
						{
							parent->_left = cur->_left;
						}
						else
						{
							parent->_right = cur->_left;
						}
					}

					delete cur;
					cur = nullptr;
				}
				else
				{
					Node* minParent = cur;
					Node* min = cur->_right;
					while (min->_left)
					{
						minParent = min;
						min = min->_left;
					}

					swap(cur->_key, min->_key);

					if (minParent->_left == min)
					{
						minParent->_left = min->_right;
					}
					else
					{
						minParent->_right = min->_right;
					}

					delete min;
					min = nullptr;
				}

				return true;
			}
		}

		return false;
	}

4）InOder()

使用二叉树的中序遍历--midorder traverse

特点：

中序遍历后的值排列是有序的

    void InOrder()
    {
		_InOrder(_root);
		return;
    }

	void _InOrder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}

		_InOrder(root->_left);
		cout << root->_key << " ";
		_InOrder(root->_right);
	}

5）BSTree(const BSTree<K>& t) 拷贝构造

使用前序遍历构造


	BSTree(const BSTree<K>& t)
	{
		_Copy(t._root);
	}

    Node* _Copy(Node* root) // 使用前序遍历构造
	{
		if (root == nullptr)
		{
			return;
		}

		Node* copyRoot = new Node(root->_key);
		copyRoot->_left = _Copy(root->_left);
		copyRoot->_left = _Copy(root->_right);
		return copyRoot;
	}