目录
1、题目描述:
2、思路1:动态规划
2.1、确定dp数组及下标含义
2.2、递推公式
2.3、初始化dp数组
2.4、确定遍历顺序
2.5、C++实现如下
3、思路2:暴力法-空间换时间
1、题目描述:
新学期伊始,适逢顿顿书城有购书满 x 元包邮的活动,小 P 同学欣然前往准备买些参考书。
一番浏览后,小 P 初步筛选出 n 本书加入购物车中,其中第 i 本(1≤ i ≤ n)的价格为 a[i] 元。
考虑到预算有限,在最终付款前小 P 决定再从购物车中删去几本书(也可以不删),使得剩余图书的价格总和 sum 在满足包邮条件(sum ≥ x)的前提下最小。
试帮助小 P 计算,最终选购哪些书可以在凑够 x 元包邮的前提下花费最小?
输入格式:
从标准输入读入数据。
输入的第一行包含空格分隔的两个正整数 n 和 x ,分别表示购物车中图书数量和包邮条件。
接下来输入 n 行,其中第 i 行(1≤ i ≤ n)仅包含一个正整数 a[i],表示购物车中第 i 本书的价格。输入数据保证 n 本书的价格总和不小于 x 。
输出格式:
输出到标准输出。
仅输出一个正整数,表示在满足包邮条件下的最小花费。
示例:
样例1输入
4 100
20
90
60
60样例1输出
110样例1解释
购买前两本书(20+90)即可包邮且花费最小。
样例2输入
3 30
15
40
30样例2输出
30样例2解释
仅购买第三本书恰好可以满足包邮条件。
样例3输入
2 90
50
50样例3输出
100样例3解释
必须全部购买才能包邮。
2、思路1:动态规划
阅读题目可以发现,题目要求选择满足包邮条件下的最小花费,听起来很像01背包相关的问题,与常规的01背包问题不同的是,背包的大小似乎是变化的,以往做的题目都是确定 一个条件选择满足的最大值,但该题目要求选择的是满足条件下的最小的值,所以第一次做这个题目的时候只得了95分,最后还是超时了五分,因为我将背包大小设置为x,先判断背包大小为x时能否装满价值等于x的书,如果不行就逐个增加背包的大小再重新判断,所以需要执行很多次循环,也就超时了。
题目比较巧妙的地方是,他将条件进行了转换,如果我们反着思考,背包的大小为sum-x,当背包大小为sum-x时能装的最大价值为ex,而ex这个数值一定是小于等于x的,因为此题目中,书籍的质量与价值相等,所以sum-ex即为满足包邮条件的最小花费,理清了思路代码实现非常简单,即经典的01背包问题。
2.1、确定dp数组及下标含义
dp[i]表示大小为i的背包能放最大价值为dp[i]的书
2.2、递推公式
dp[j] = max(dp[j],dp[j-a[i]]+a[i]);
2.3、初始化dp数组
dp[0]表示背包大小为0时能放下多少书,根据题目描述,dp[0]自然是0,而其他的dp数组初始化为最小非负数即可。
2.4、确定遍历顺序
外层遍历物品从前往后,内层遍历背包从大到小
2.5、C++实现如下
#include<iostream>
#include<algorithm>
using namespace std;
int main() {
int n,x;
cin>>n>>x;
int a[n];
int sum = 0;
for(int i = 0; i<n; ++i) {
cin>>a[i];
sum+=a[i];
}
int target = sum-x;
vector<int> dp(target+1,0);
for(int i = 0; i<n; ++i) {
for(int j = target; j>=a[i]; --j) {
dp[j] = max(dp[j],dp[j-a[i]]+a[i]);
}
}
cout << sum-dp[target];
return 0;
}3、思路2:暴力法-空间换时间
遍历每一本书,每次选择买与不买,将每本书买与不买的花费存到set容器中,那么最后一个set容器中将保存每一种情况的花费,而set内部又是存在排序的,这样时间复杂度优化为O(n)。
考试的时候写不下去可以往空间换时间的角度来思考。
#include<iostream>
#include<set>
using namespace std;
int main() {
int n,x;
cin>>n>>x;
int a[n+1];
int sum = 0;
for(int i = 1; i<=n; ++i) {
cin>>a[i];
sum+=a[i];
}
set<int> s[n+1];
s[0].insert(0);
for(int i = 1;i<=n;++i){
set<int>::iterator it = s[i-1].begin();
for(it;it!=s[i-1].end();++it){
int buy = *it+a[i];
int noBuy = *it;
s[i].insert(buy);
s[i].insert(noBuy);
}
}
set<int>::iterator it = s[n].begin();
for(it;it!=s[n].end();++it){
if(*it>=x){
cout << *it << endl;
break;
}
}
return 0;
}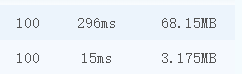
根据运行结果我们也可以看出该题使用了空间换时间的策略,但也是可以得到100分的。